Abstract
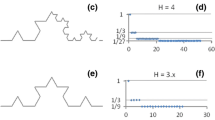
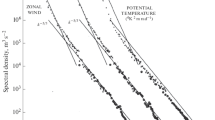
Fractal analysis and Fourier analysis are independent techniques for quantitatively describing the variability of natural figures. Both methods have been applied to a variety of natural phenomena. Previous analytical work has formulated relationships between the fractal dimension and power law form frequency spectrum.Mandelbrot (1985) has shown that difficulties arise when the ruler method for measuring dimensionality is applied to other than self-similar figures. Since an investigator presumably does not know in advance the dimensionality of a natural profile, it is essential to quantify the nature of the discrepancy for self-affine cases. In this study, a series of experiments are conducted in which discrete random series of specified spectral forms are analyzed using the fractal ruler method. The various parameters of the fractal measurement are related to the parameters of the spectral model. In this way, empirical relationships between the techniques can be derived for discrete, finite series which simulate the results of applying the fractal method to observational data.
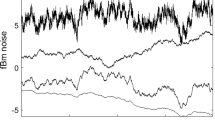
The results of the study indicate that there are considerable discrepancies between the results predicted by theory and those derived empirically. The fundamental power law form of length versus resolution pairs does not hold over the entire region of analysis. The predicted linear relationship between fractal dimension and exponent of the frequency spectrum does not hold, and the spectral signals can be extended beyond the limits of dimension inferred by theory. Root-mean-square variability is also shown to be linearly related to the fractal intercept term. An investigation of the effect of nonstationary sampling is conducted by generating signals composed of segments of differing spectral characteristics. Fractal analyses of these signals appear identical to those conducted on stationary series.
The discrepancies between theoretical prediction and empirical results described in this study reflect the difficulties of applying analytically derived techniques to measurement data. Both Fourier and fractal techniques are formulated through rigorous mathematics, assuming various conditions for the underlying signal. When these techniques are applied to discrete, finite length, nonstationary series, certain statistical transformations must be applied to the data. Methods such as windowing, prewhitening, and anti-aliasing filters have been developed over many years for use with Fourier analysis. At present, no such statistical theory exists for use with fractal analysis. It is apparent from the results of this study that such a statistical foundation is required before the fractal ruler method can be routinely applied to observational data.
Similar content being viewed by others
References
Aviles, C. A., Scholtz, C. H., andBoatwright, J. (1987),Fractal Analysis Applied to Characteristic Segments of the San Andreas Fault, Journal of Geophysical Research92 (BI), 331–344.
Barenblatt, G. I., Zhivago, A. V., Neprochnov, Yu. P., andOstrovskiy A. A. (1984),The Fractal Dimension: A Quantitative Characteristic of Ocean-bottom Relief, Oceanology24 (6), 695–697.
Bell, T. H. (1975),Statistical Features of Sea-Floor Topography, Deep-Sea Research22, 883–892.
Berry, M. V. andLewis, Z. V. (1980),On the Weierstrass-Mandelbrot Fractal Function, Proceedings of the Royal Society of LondonA 370, 459–484.
Bloomfield, P. R.,Fcurier Analysis of Time Series: An Introduction (John Wiley and Sons, New York 1976), pp. 258.
Bracewell, R. N.,The Fourier Transform and its Applications (McGraw-Hill, New York 1978), pp. 381.
Brown, S. R. (1987),A Note on the Description of Surface Roughness Using Fractal Dimension, Geophysical Research Letters, (submitted).
Brown, S., andScholtz, C. H. 1985,Broad Bandwidth Study of the Topography of Natural Rock Surfaces, Journal of Geophysical Research90 (12), 12,575–12,582.
Chatfield, C.,The Analysis of Time Series: An Introduction (Chapman and Hill, New York 1980) pp. 268.
Fox, C. G. (1987),An Inverse Fourier Transform Algorithm for Generating Random Signals of a Specified Spectral Form, Computers and Geoscience13 (3), 1–6.
Fox, C. G. (1985),Description, Analysis and Prediction of Sea-floor Roughness Using Spectral Models, Naval Oceanographic Office Technical Report279, Bay St. Louis, MS., pp. 218.
Fox, C. G., andHayes, D. E. (1985),Quantitative Methods for Analyzing the Roughness of the Seafloor, Reviews of the Geophysics and Space Physics23 (1), 1–48.
Mandelbrot, B. B. (1985),Self-affine Fractals and Fractal Dimension, Physica Scripta32, 257–260.
Mandelbrot, B. B.,The Fractal Geometry of Nature, (W. H. Freeman, San Francisco, CA 1982), pp. 460.
Mandelbrot, B. B. (1967),How Long is the Coastline of Britain? Statistical Self-similarity and Fractal Dimension, Science155, 636–638.
Oppenheim, A. V., andLin, J. S. (1981),The Importance of Phase in Signals, Proceedings of the IEEE69 (5), 529–541.
Sayles, R. S., andThomas, T. R. (1978),Surface Topography as a Nonstationary Random Process, Nature271, 431–434.
Scarborough, J. B.,Numerical Mathematical Analysis (The Johns Hopkins Press, Baltimore, MD 1930) pp. 46.
Scholz, C. H., andAviles, C. A. (1986),The fractal geometry of faults and faulting, InEarthquake Source Mechanics, Geophysical Monograph37, 147–155.
Wong, P.,Fractal surfaces in porous media, inPhysics and Chemistry of Porous Media III, AIP Conference Proceedings, 154 (eds. Banavar, J., Koplik, J., and Winkler, K.) (Amer. Inst. Phys., New York 1987) pp. 304–318.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Fox, C.G. Empirically derived relationships between fractal dimension and power law form frequency spectra. PAGEOPH 131, 211–239 (1989). https://doi.org/10.1007/BF00874488
Received:
Revised:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF00874488