Simulation of the spherical aberration of focused laser radiation in transparent materials: comparison of different simulation approaches

Abstract

Creating microvoids, cracks or refractive index modifications within dielectrics focusing intense laser radiation into the transparent material offers many promising applications, such as holographic data storage, laser-written waveguides or optical gratings. For further improvements in the quality of the named applications, a deep understanding of the involved processes during interaction of laser radiation with material is necessary. In this work, the change in the laser intensity distribution of focused laser radiation into PMMA by spherical aberration, caused by the transition of the radiation from air to matter, is discussed. Theoretical and numerical investigations including nonlinear effects of laser radiation material interaction as well as multi-physical approaches, such as combined calculation of the beam propagation, the temperature distribution and induced tensions, require a lot of effort and long computation time. Therefore, simple linear simulations are performed including calculation of the beam propagation without nonlinear optical effects, like self-focusing. Comparing the calculated intensity distributions with experimental data, regarding the lateral and axial size as well as the position of the laser-generated voids within PMMA, the applicability of the simulation approaches is demonstrated. The different simulation approaches are characterized in regard to their calculation time and accuracy depending on the simulation task.

Appendix: Simulation methods

1.1 Kirchhoff’s diffraction formula (KDF)

Kirchhoff’s diffraction formula represents a calculation method in the field of scalar diffraction theory and is based on the mathematical formulation of Huygens principle. The electric field strength can be calculated by

$$\begin{aligned} E_1 (x_1,y_1,z_1 )&= \frac{n_0}{{\mathrm {i}}\cdot \lambda _0} \oint _{A_0}\frac{E_0 (x_0, y_0, z_0 )}{r}\cdot {\mathrm {e}}^{{\mathrm {i}}\cdot n_0\cdot k_0\cdot r} \\&\quad \cdot N (x_0,y_0,z_0 )~{\mathrm {d}}A_0. \end{aligned}$$

(4)

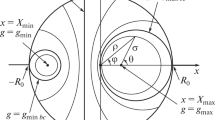
The used parameters are visualized in Fig. 9. $A_0$ represents the source plane for elementary waves with the incident complex electrical field $E_0$ and $A_1$ represents the target plane with the electric field strength $E_1$. The elementary waves are represented by the terms $\frac{E_0 (x_0,y_0,z_0)}{r}\cdot {\mathrm {e}}^{{\mathrm {i}}\cdot n_0\cdot k_0\cdot r}$, where

$$\begin{aligned} r=\sqrt{(x_0-x_1 )^2+(y_0-y_1 )^2+(z_0-z_1 )^2 } \end{aligned}$$

(5)

represents the distance between point $P_0 (x_0;y_0;z_0 )$ on the plane $A_0$ and point $P_1 (x_1;y_1;z_1 )$ on the plane $A_1$ [13, 14]. The form and position of the two planes can be chosen arbitrarily. $\mathbf {k}$ represents the wave vector of the incident wave at point $P_0$, with the wave number $k_0=\frac{2\cdot {\pi }}{\lambda _0}$, $\lambda _0$ the wavelength of the radiation in vacuum, $n_0$ the refractive index between plane $A_0$ and $A_1$, $\mathbf {n}$ the normal vector at point $P_0$. N represents the slope factor and can be calculated by $N(x_0, y_0, z_0) = \frac{1}{2}(\cos (\mathbf {n},\mathbf {r})-(\cos (\mathbf {n},\mathbf {k}))$.

Fig. 9

Schematic representation of the used planes and variables

In most of the cases, the distance of $A_1$ to $A_0$ is large enough to neglect any dependency on N, therefore $N\approx 1$. The summation of all elementary waves is mathematically realized by the integration over the plane $A_0$.

1.2 Angular spectrum of plane waves (SPW)

In the case that the planes $A_0$ and $A_1$ are both perpendicular to the propagation direction, and having the same sampling, the SPW can be applied [13, 14]. The electric field strength $E_1$ is calculated by the Fourier transform ${\mathcal {F}}$ according to

$$\begin{aligned} E_1={\mathcal {F}}^{-1}\left( {\mathcal {F}}(E_0)\cdot {\mathrm {e}}^{2\cdot{\pi }\cdot\mathrm{i} \cdot {\Delta }z\cdot \sqrt{ \frac{n_0^2}{\lambda _0^2} -(\nu _x^2 + \nu _y^2) }}\right) . \end{aligned}$$

(6)

$\nu _x$ and $\nu _y$ represent the spatial frequencies used for the fourier transform and can be calculated by ${\Delta }x\cdot {\Delta }\nu _x =\frac{1}{N_x}$ and $\nu _x=-\frac{N_x}{2}{\Delta }\nu _x\ldots \frac{N_x}{2}{\Delta }\nu _x$. KDF and SPW represents a BEM.

1.3 Finite-difference time-domain (FDTD)

The simplest form of FDTD includes only Faraday’s law

$$\begin{aligned} \nabla \times \mathbf {E}=-\sigma _{\rm m}\cdot \mathbf {H} -\mu \cdot \frac{\partial \mathbf {H}}{\partial t}, \end{aligned}$$

(7)

and Ampère’s law [15–17]

$$\begin{aligned} \nabla \times \mathbf {H}=\sigma \cdot \mathbf {E} -\varepsilon \cdot \frac{\partial \mathbf {E}}{\partial t}. \end{aligned}$$

(8)

$\sigma _\mathrm{m}$ represents the magnetic conductivity, $\sigma$ the electric conductivity, $\mu$ the permeability, $\varepsilon$ the permittivity and $\mathbf {H}$ the magnetic field strength. Equations (7) and (8) are discretized using finite differences. The derivations are solved by a convolution of the data matrices of each field and a convolution kernel as widely used in digital image processing [18].

1.4 Symmetry and locations of planes used by the simulation methods

The used simulations methods can be subdivided resulting from to the considered symmetry. On each plane, there are $N_x$ elements in $x-$direction and $N_y$ elements in $y-$direction, respectively. Plane $A_0$ has the subindex $i=0$ and plane $A_1$ has the subindex $i=1$. The total number of elements per matrix $N_{\mathrm{tot}}$ on each plane is $N_{\mathrm{tot }_i} = N_{x_i} \cdot N_{y_i}$ (Fig. 10).

Fig. 10

Schematic representation of the used elements on plane $A_0$ and $A_1$

If no symmetry can be used for BEM, all elements of plane $A_0$ and $A_1$ have to be considered. These methods are marked with 2D. In the case of considering axially symmetric intensity distributions, only the calculation of the intensity along a half coordinate axis, e. g. the $x-$axis beginning from element 1 up to $N_{x_1} / 2$, on plane $A_1$ is necessary. In this case, the calculation methods are marked with 2Da. Furthermore, for a spatial gaussian beam intensity distribution, the source plane $A_0$ can be a line too. Therefore, the methods are called 1D methods. The total number of elements, resulting from the considered symmetry, are summarized in Table 2.

For KDF, the location of the target plane $A_1$ is very flexible and the x–z plane or the y–z plane are often used as $A_1$. In contrast to KDF and SPW, for FDTD the whole area has to be discretized. The discretization includes $x-, y-,$ and $z-$coordinates of the area. If only the x–z plane or the y–z plane is considered, FDTD is marked with 2D, and neglects the third dimension. By taking advantage of axial symmetry, the differential operators in Eqs. (7) and (8) can be formulated in cylindrical coordinates and all dimensions are included. Therefore, the addition is 2Da.

Table 2 Summary of the used elements for BEM