Abstract
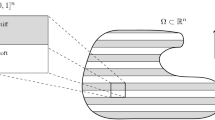
Given an open bounded connected set Ω ⊂R N and a prescribed amount of two homogeneous materials of different density, for smallk we characterize the distribution of the two materials in Ω that extremizes thekth eigenvalue of the resulting clamped membrane. We show that these extremizers vary continuously with the proportion of the two constituents. The characterization of the extremizers in terms of level sets of associated eigenfunctions provides geometric information on their respective interfaces. Each of these results generalizes toN dimensions the now classical one-dimensional work of M. G. Krein.
Similar content being viewed by others
References
Attouch, H., Variational Convergence for Functions and Operators, Pitman, Boston, 1984.
Auchmuty, G., Dual variational principles for eigenvalue problems, in Nonlinear Functional Analysis and Its Applications, F. Browder, ed., American Mathematical Society, Providence, RI, 1986, pp. 55–71.
Barbu, V., and Precupanu, T., Convexity and Optimization in Banach Spaces, Reidel, Boston, 1986.
Boccardo, L., and Marcellini, P., Sulla convergenza delle soluzioni di disequazioni variazionali, Ann. Mat. Pura Appl. 4(110), 1977, pp. 137–159.
Bourbaki, N., Topological Vector Spaces, Springer-Verlag, New York, 1987, Chapters 1–5.
Brezis, H., Analyse Fonctionelle, Masson, Paris, 1983.
Cea, J., and Malanowski, K., An example of a max-min problem in partial differential equations, SIAM J. Control 8(3), 1970, pp. 305–316.
Cosner C., and Schmitt, K., On the geometry of the level sets of positive solutions of semilinear elliptic equations, Rocky Mountain J. Math. 18(2), 1988, pp. 277–286.
Ekeland, I., and Temam, R., Convex Analysis and Variational Problems, North-Holland, Amsterdam, 1976.
Friedland, S., Extremal eigenvalue problems defined for certain classes of functions, Arch. Rational Mech. Anal., 67(1), 1977, pp. 73–81.
Gidas, B., Ni, W., and Nirenberg L., Symmetry and related properties via the maximum principle, Comm. Math. Phys. 68, 1979, pp. 209–243.
Gilbarg, D., and Trudinger, N., Elliptic Partial Differential Equations of Second Order, Springer-Verlag, New York, 1983.
Jouron, C., Sur un problème d'optimisation ou la contrainte porte sur la fréquence fondamentale, RAIRO Anal. Numèr. 12(4), 1978, pp. 349–374.
Kato, T., Perturbation Theory for Linear Operators, Springer-Verlag, New York, 1984.
Kawohl, B., Rearrangements and Convexity of Level Sets in PDE, Springer-Verlag, New York, 1985.
Kesavan, S., Homogenization of elliptic eigenvalue problems I, Appl. Math. Optim. 5, 1979, pp. 153–167.
Knaster, B., Kuratowski, C., and Mazurkiewicz, S., Eine beweis des fixpunksatzes fürn-dimensionale simplexe, Fund. Math. 14, 1929 pp. 132–137.
Kohn, R., and Strang, G., Optimal design and relaxation of variational problems I, II, III, Comm. Pure Appl. Math. 39, 1986, pp. 113–137, 139–182, and 353–377.
Krein, M. G., On certain problems on the maximum and minimum of characteristic values and on the Lyapunov zones of stability, AMS Translations Ser. 2(1), 1955, pp. 163–187.
Mikhlin, S. G., Variational Methods in Mathematical Physics, Macmillan, New York, 1964.
Olhoff, N., Optimal design with respect to structural eigenvalues, Proc. 15th Int. Congress of Theoretical and Applied Mechanics, 1980, Rimrott and Tabarrok, eds., North-Holland, Amsterdam, 1980, pp. 133–149.
Roberts, A., and Varberg, D., Convex Functions, Academic Press, New York, 1973.
Stuart, C. A., and Toland, J. F., A variational method for boundary value problems with discontinuous nonlinearities, London Math. Soc. 2(21), 1980, pp. 319–328.
Tahraoui, R., Quelques remarques sur le controle des valeurs propres, in Nonlinear PDE's and Their Applications, College de France Seminar, Volume VIII, H. Brezis and J. L. Lions, eds. Longman, Essex, 1988, pp. 176–213.
Tartar, L., Compensated compactness and applications to partial differential equations, in Nonlinear Analysis and Mechanics, Heriot-Watt Symposium IV, R. J. Knops, ed., Pitman, London, 1979.
Treves, F., Basic Linear Partial Differential Equations, Academic Press, New York, 1975.
Author information
Authors and Affiliations
Additional information
Communicated by D. Kinderlehrer
The work of the first author was supported in part by NSF Grant DMS-8201719 (A. Manitius, P. I.), an IBM fellowship, a GE teaching incentive, and DARPA Contract F49620-87-C-0065. That of the second author was supported in part by ONR Grant N00014-84-5-516, AFOSR Grant AFOSR-86-0180, and NSF Grant DMS-8713722.
Rights and permissions
About this article
Cite this article
Cox, S.J., McLaughlin, J.R. Extremal eigenvalue problems for composite membranes, II. Appl Math Optim 22, 169–187 (1990). https://doi.org/10.1007/BF01447326
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF01447326