The proton charge radius extracted from the initial-state radiation experiment at MAMI

Abstract

We report on a comprehensive reinterpretation of the existing cross-section data for elastic electron-proton scattering obtained by the initial-state radiation technique, resulting in a significantly improved accuracy of the extracted proton charge radius. By refining the external energy corrections we have achieved an outstanding description of the radiative tail, essential for a detailed investigation of the proton finite-size effects on the measured cross sections. This development, together with a novel framework for determining the radius, based on a regression analysis of the cross sections employing a polynomial model for the form factor, led us to a new value for the charge radius, which is $(0.878 \pm 0.011_\mathrm {stat.}\pm 0.031_\mathrm {sys.}\pm 0.002_\mathrm {mod.})\,\mathrm {fm}$

1 Introduction

The problem of the proton charge radius arose from the significant deviation of the very precise Lamb shift measurements in muonic hydrogen [1, 2], which gave a value of $0.84087(39)\,\mathrm {fm}$, from the CODATA [3] value of $0.8751(61)\,\mathrm {fm}$, compiled from electron scattering and the old atomic Lamb shift measurements. This discrepancy has motivated several follow-up measurements, but despite the efforts remains unresolved. While the measurement of the 2S–4P transition in hydrogen [4] and the new scattering experiment at Jefferson Lab [5] yield values of $0.8335(95)\,\mathrm {fm}$ and $0.831(14)\,\mathrm {fm}$, which are in agreement with the smaller radius, the measurement of the 1S–3S transition [6] gives a value of $0.877(13)\,\mathrm {fm}$, and supports previous scattering experiments [7, 8] and the hypothesis of a large proton radius. Therefore, additional experiments, both scattering and spectroscopic, still have the potential to make valuable contributions to the proton size problem [9, 10].

In scattering experiments the charge radius of the proton is traditionally determined by measuring the cross section for elastic scattering of electrons from hydrogen, which depends on $G_E^p$ and carries information about the charge distribution of the proton. The proton charge radius, $r_p$, is given by

$$\begin{aligned} r_p^2 \equiv \left. -6\hbar ^2 \frac{\mathrm {d}G_E^p}{\mathrm {d}Q^2}\right| _{Q^2=0}\,, \end{aligned}$$

(1)

where $Q^2$ is the absolute value of the square of the four-momentum transfer to the proton. The accuracy of the radius obtained in this manner is limited by the extent of available data sets, which dictates the approach to the extrapolation of $G_E^p$ needed to determine the slope at $Q^2=0$. Hence, to ensure a reliable extraction of the radius, measurements of $G_E^p$ are needed in the region of $Q^2\lesssim 0.01\,\mathrm {GeV}^2/c^2$.

Efforts to perform such measurements with the standard approaches are limited by the minimum $Q^2$ accessible with the experimental apparatus at hand, predominantly due to the restrictions in the available electron beam energy and the minimum scattering angle. Therefore, a new experimental approach based on initial-state radiation has been introduced [11] that allows for cross-section measurements down to $0.001\,\mathrm {GeV^2}/c^2$ with sub-percent precision by using information about the charge form factor that is implicit in the radiative tail of the elastic peak.

2 Initial-state radiation experiment

The radiative tail of an elastic peak is dominated by the coherent sum of two Bethe-Heitler diagrams [12] shown in Fig. 1. The initial-state radiation diagram (BH-i) describes the process where the incident electron emits a real photon before interacting with the proton. Since the emitted photon carries away a fraction of the incident energy, the momentum transfer to the proton is decreased. Hence, this process probes the proton structure at values of $Q^2$ smaller than the value fixed by the experimental kinematics and is thus sensitive to the form factors at $Q^2$ smaller than those corresponding to the elastic setting. On the other hand, the final state radiation diagram (BH-f) corresponds to the reaction where the real photon is emitted after the interaction with the nucleon. Consequently, $Q^2$ at the vertex remains constant, while the detected four-momentum transfer changes.

Fig. 1

Measured and simulated elastic peak with the corresponding radiative tail for the kinematic setting at $495\,\mathrm {MeV}$. See [11] for details. The radiative tail is dominated by the two Bethe-Heitler diagrams (BH-i and BH-f), where electrons emit real photons before or after the interaction with the protons. The grey band marks the position and width of the elastic line inside the spectrometer acceptance

In an inclusive experiment $Q^2$ can not be measured directly, which means that looking only at the data the initial-state radiation processes cannot be distinguished from the final state radiation. Hence, in order to get information on $G_E^{p}$ at $Q^2$ smaller than the elastic setting, the data must be studied in conjunction with a Monte-Carlo simulation, which includes a detailed description of internal radiative corrections and considers $G_E^{p}$ as its free parameter. This is the basic idea of the MAMI experiment, which opened the door of obtaining $G_{E}^{p}$ down to $Q^2 \simeq 10^{-4}\,\mathrm {GeV^2}/c^2$ [11].

The measurement of the radiative tail has been performed at the Mainz Microtron (MAMI) in 2013 using the spectrometer setup of the A1-Collaboration [13]. A rastered electron beam with energies of $E_0=195$, 330 and $495\,\mathrm {MeV}$ was used in combination with a hydrogen target, which consisted of a $5\,\mathrm {cm}$ long cigar-shaped Havar cell filled with liquid hydrogen and placed in an evacuated scattering chamber. For the cross-section measurements the single-dipole magnetic spectrometer B was operated at a fixed angle of $15.21^\circ$, while its momentum settings were adjusted to scan the complete radiative tail for each beam energy. The central momentum of each setting was measured with an NMR probe to a relative accuracy of $8\times 10^{-5}$. The spectrometer was equipped with the standard detector package consisting of two layers of vertical drift chambers (VDCs) for tracking, two layers of scintillation detectors for triggering, and a threshold Cherenkov detector for particle identification. The kinematic settings of the experiment were chosen such that the radiative tails scanned at three beam energies overlap.

The beam current was between $10\,\mathrm {nA}$ and $1\,\mu \mathrm {A}$ and was limited by the maximum rate allowed in the VDCs ($\approx 1\,\mathrm {kHz/wire}$), resulting in raw rates up to $20\,\mathrm {kHz}$. The beam current was determined by a non-invasive fluxgate-magnetometer and from the collected charge of the beam stopped in a Faraday cup. At low beam currents and low beam energies the accuracy of both approaches is not better than $2\,\mathrm {\%}$, which is insufficient for precise cross-section measurements. Hence spectrometer A was used at a fixed momentum and angular setting for precise monitoring of the relative luminosity.

The first analysis of the data, presented in [11], revealed inconsistencies between data and simulation on the order of $10\,{\%}$ at the top of the elastic peak, see Fig. 2, which led to the omission of the most statistically relevant, elastic data points in the analysed sample. The inconsistency arose due to the incomplete correction for the electron energy losses in the target material. To be able to incorporate the elastic data in the analysis and ensure a more precise extraction of the proton charge radius, the estimations of the external corrections had been investigated in detail.

Fig. 2

Top: Due to the imperfect vacuum conditions inside the scattering chamber, the residual molecules of nitrogen and oxygen gather on top of the cold target, forming a thin film of cryogenic depositions. The thickness of the layer on the side walls ($d_\mathrm {away}$) is much thicker than the layer on the end caps ($d_\mathrm {along}$) exposed to the beam. Bottom: Relative differences between the data and simulations for the first experimental setup at $495\,\mathrm {MeV}$, including data at the elastic peak and first part of the radiative tail. The blue line shows the original comparison considered in [11], when the simulation assumes a uniform layer of cryogens around the target cell. The inconsistency between the data and simulation, which affects the trend of the ratio in the first $5\,\mathrm {MeV}$ of the radiative tail, is evidence that the layer of cryogens away from the beam is significantly thicker than along the beam. The black, green and red lines demonstrate the ratios, when the layer on the side walls is 200-, 400- and 600-times thicker than on the end caps. For the $495\,\mathrm {MeV}$ setting the analysis determined the best ratio between the amount of cryogenic deposits on the side walls and on the end caps to be $180\pm 10$. The systematic uncertainty of all the points is $0.5\,{\%}$. The grey band marks the position and width of the elastic line inside the spectrometer acceptance

The external radiative corrections were considered using the formalism of Mo and Tsai [14], while the collisional corrections were approximated by the Landau distribution [15]. The uncertainty of the applied energy corrections was estimated to be smaller than $1\,\%$ [14]. This was confirmed by the dedicated calibration data collected using plastic ($[\mathrm {CH_2}]_n$) targets with different thicknesses, which created a perfect testbed for validating the applied corrections, since the spectra differ only in the size of the external energy loss correction. The comparison of the elastic peak shapes for different target thicknesses with the simulations presented the correct scaling of the corrections with the thickness of the target.

The impact of the external radiative and collisional corrections on the shape of the radiative tail is observable only in the first few $\mathrm {MeV}$ of the radiative tail, see Fig. 2. Hence, an inconsistency between the data and simulation in this region is an indication of an unaccounted for material traversed by the electrons. These inconsistencies are related to the traces of cryogenic deposits on the end caps and side walls of the target cell. They consist mostly of residual nitrogen and oxygen still present in the scattering chamber in spite of the good vacuum conditions ($10^{-6}\,\mathrm {mbar}$) [16]. The extra material affects the measured spectra and thus needs to be included in the simulation. This requires knowing the amount of cryogenic deposits at the target walls. The thickness of the depositions on the target entrance window was determined using the nitrogen/oxygen elastic data. Since this wall is exposed to the electron beam, the electrons scattered from the cryogens enter the physics spectra and can be monitored. For this purpose spectrometer A was positioned such that the nitrogen/oxygen elastic lines were inside its acceptance. The collected spectra, together with the known elastic cross sections for these elements were used to determine the thickness of the deposited layer. On the other hand, incident electrons do not scatter from the material on the side walls, hence the cryogens there are not directly detectable by the spectrometers. Furthermore, depositions on the side walls can be much thicker than those on the end caps, because the former are not heated by the electron beam. The amount of cryogens there was estimated by matching the functional dependence of the simulation to the measured elastic spectra, which is uniquely correlated to the thickness of the traversed material, see Fig. 2. The analysis has shown that the layer of cryogens on the side can be as much as 200 times thicker (roughly $4\cdot 10^{-3}\,\mathrm {g/cm^2}$) than at the end caps.

With this advancement the agreement between the data and simulation improved significantly and allowed us to include the elastic data in the new analysis presented in this paper. Following the approach described in [11] the full set of 25 data points could then be used to extract the proton-charge form factors for $0.001 \le Q^2 \le 0.017\,\mathrm {GeV}^2/c^2$. The values and the details of the extraction are presented in Appendix B of this paper.

3 Experimental uncertainties

Although the ISR experiment provides remarkable control over the systematic uncertainties [11], a few ambiguities remain and limit the precision of the measurements. The contributions relevant for the extraction of the proton charge radius include the uncertainty in the relative luminosity ($0.2\,{\%}$), the uncertainty in the detector efficiencies $(0.2\, {\%})$ and the contamination coming from the target support frame and the spectrometer entrance flange $(\lesssim 0.7\, {\%})$. The uncertainty of the data associated by the contamination of the spectra with the cryogenic depositions was assessed using a dedicated simulation, normalized to the intensity of the nitrogen, oxygen and Havar elastic lines in the measured spectra. The relative uncertainty of the simulation was estimated to be $5\,\%$, which leads to a $0.1\,\%-1.1\,\%$ uncertainty of the measured cross-section ratios. For further details see Appendix A.

4 Parameterisation of the form factor

For $Q^2<0.02\,\mathrm {GeV}^2/c^2$ it suffices for all practical purposes to parameterise the measured proton charge form factor by using a polynomial of the form

$$\begin{aligned} G(Q^2)= n_{E_0}\left[ 1 - \frac{r_p^2\,Q^2}{6\,\hbar ^2} + \frac{a\,Q^4}{120\,\hbar ^4} - \frac{b\,Q^6}{5040\,\hbar ^6}\right] \,, \end{aligned}$$

(2)

where $n_{E_0}$ represents the normalisation of the data, $r_p$ represents the radius and a and b are the higher moments of the model. Although the $Q^4$- and $Q^6$-terms at $Q^2<0.02\,\mathrm {GeV}^2/c^2$ account for only about a percent of the form-factor value, they need to be considered in the fit. Due to a strong correlation between radius and a (b), which was estimated to be 0.97 (0.92), a wrong choice of these parameters could shift the value of the radius at the level of $0.01 (0.003)\,\mathrm {fm}$, see Fig. 3. The data in the available $Q^2$ range (even with a superior experimental precision) do not permit simultaneous determination of all three parameters [17]. Therefore, a and b need to be taken from the literature. To minimise the bias of the extracted radius, we considered values obtained from the analysis of the available world data [18] which are consistent with the latest experimental results from Jefferson Lab [5]:

$$\begin{aligned} a=(2.59\pm 0.194)\,\mathrm {fm}^4\,,\qquad b=(29.8\pm 14.71)\,\mathrm {fm}^6\,. \end{aligned}$$

(3)

Fig. 3

The proton charge radius, $r_p$, extracted from the data using Eq. (2), depends on the value of the parameter a in accordance with the full black line. The red line and the error band show the value of the parameter a determined by Sick et al. [17]. The orange line with the corresponding uncertainty band shows the result extracted from the most recent experiment at Jefferson Lab [5]. The blue vertical line and the corresponding uncertainty band demonstrate the value obtained by Distler et al. [18] who performed a comprehensive analysis of world data until 2010. Relying on the authors’ value for this parameter, the green band surrounding the green dashed line denotes the model uncertainty of the radius extracted in this experiment

5 Original determination of the radius

The prevailing way of determining the proton charge radius is by comparing the measured sets of proton-charge form factors with a selected model. Following the steps in [11] the data were fit by a polynomial (2), by using a common parameter for the radius, $r_p$, and different normalisation factors, $n_{E_0}$, one for each energy, see Appendix B for details. In terms of this fit with 21 degrees of freedom, the radius was determined to be $r_p = (0.873 \pm 0.017_{\mathrm {stat.}} \pm 0.059_{\mathrm {syst.}} \pm 0.003_\mathrm {mod.})\,\mathrm {fm}\,$. The value of $\chi ^2$, when both statistical and systematical uncertainties are considered, equals 17.7 and remains comparable to the value of 15.8 obtained with the previous dataset [11]. However, even by improving the analysis in the manner described above, the extracted radius still depends critically on the available $Q^2$ range and the number of fitting parameters. It also remains burdened by large systematic uncertainties of the measured cross-section ratios. The systematic uncertainty is a combination of the experimental uncertainties, presented in Sect. 3, and the uncertainties of the simulation employed to calculate the radiative tail of the elastic peak, which are presented in Appendix A.

Fig. 4

Relative differences between the data and simulations for $495\,\mathrm {MeV}$ (top) and $330\,\mathrm {MeV}$ (bottom) settings. Each set of ratios corresponds to simulations with a different value of the proton charge radius $r_p = 0.76\,\mathrm {fm}$ (blue), $0.85\,\mathrm {fm}$ (black), $0.95\,\mathrm {fm}$ (green) and $1.05\,\mathrm {fm}$ (red). The ratios are normalised to the first (elastic) point and are artificially offset from zero (denoted by the thin dashed line) for clarity. The corresponding lines show linear fits to the data. The grey bands drawn around ratios for $r_p=0.85\,\mathrm {fm}$ demonstrate the combined uncertainty (statistical and systematical added in quadrature) of the extracted slope parameter $k(r_p)$. Black boxes at the bottom of each plot demonstrate the systematic uncertainties considered in the determination of the fit parameter $k(r_p)$

6 New extraction of the radius

To further improve the result within the scope of available data, an alternative approach was considered, applicable at the level of measured cross sections. In particular, we studied the ratios of measured and simulated cross sections. First, the cross-section ratios were normalised to the elastic point. To first order the $E'$ evolution of the rescaled ratios between the data and the simulation at each energy setting depends linearly on the proton charge radius. Furthermore, since all points for a single energy configuration are strongly correlated due to the nature of the experimental approach, the effect of changing the radius appears as a change of the slope of the ratio, $k(r_p)$. Relying on the chosen model (2), the simulation was performed for different values of $r_p$ between $0.76\,\mathrm {fm}$ and $1.05\,\mathrm {fm}$, and compared to the data; see Fig. 4. The results of the comparison for the two highest energy settings ($330\,\mathrm {MeV}$ and $495\,\mathrm {MeV}$) exhibit a clear dependence and sensitivity to small changes in the proton radius. On the other hand, the $Q^2$ values of the data at $195\,\mathrm {MeV}$ are so small that within the measured uncertainties these data alone demonstrate no detectable dependence on the radius and were thus excluded from the analysis.

Fig. 5

The ratio between data and simulation shown in Fig. 4 depends linearly on the energy of the scattered electron, $E'$. The slope parameter describing this linear trend, k, depends on the value of $r_p$ considered in the simulation. This figure shows how $k(r_p)$ changes with the radius for the $495\,\mathrm {MeV}$ (blue) and $330\,\mathrm {MeV}$ (green) settings. The surrounding error bands denote the combined uncertainty (statistical and systematical added in quadrature) of the slope parameter $k(r_p)$, see also Fig. 4. The point where the curve crosses zero represents a radius where the simulation best matches the data. The blue and green points (together with the corresponding uncertainties) show the best radii for the two analysed data sets. The black point represents their weighted average

The best estimate for the proton charge radius should reveal a constant ratio between the data and the simulation. The ratios presented in Fig. 4 indicate that the $495\,\mathrm {MeV}$ setting favours a radius of $\approx 0.84\,\mathrm {fm}$, while the $330\,\mathrm {MeV}$ data suggest $\approx 1.0\,\mathrm {fm}$. Finding the $r_p$ at which the simulation matches the data corresponds to finding a point where $k(r_p)=0$, see Fig. 5. The extracted radii for the two energy settings exhibit a $2.5\sigma$ tension. This could be a consequence of a statistical fluctuation, but it could also hint at underestimated or missing sources of the systematic uncertainty. These have been studied in detail, see Appendix A, but the discrepancy remained. Consequently, the proton charge radius that agrees with both data sets corresponds to the weighted average of the results for the two beam energies, which is:

$$\begin{aligned} r_p = \left( 0.878 \pm 0.011_\mathrm {stat.}\pm 0.031_\mathrm {sys.}\pm 0.002_\mathrm {mod.}\right) \,\mathrm {fm}\,. \end{aligned}$$

Following this approach, the radius is the only free parameter. By investigating the slopes, the normalisations $n_{E_0}$ disappear from the analysis, resulting in a more robust extraction of the radius, which is less sensitive to the systematic uncertainties than the original result, presented in Sect. 5. The uncertainty of the radius directly follows from the uncertainties of $k(r_p)$ shown in Figs. 4 and 5. The statistical uncertainty combines contributions of data and simulation, added in quadrature. The number of simulated events was chosen such that the simulated uncertainty is always smaller than the experimental one. The systematic uncertainty is dominated by the pointwise contributions presented in Sect. 3. The model dependent uncertainty is dominated by the uncertainty of the parameter a considered in Eq. 2 to model $G_E^p$ in the simulation, see Fig. 3.

7 Conclusions

The initial-state radiation experiment at MAMI [11] established a new method for precise investigations of the electromagnetic structure of the nucleon and underlying electromagnetic processes at extremely small $Q^2$. In this paper we present our findings on the improved data analysis, which revealed the necessity of a complete consideration of cryogens deposited on the liquid hydrogen cell and their influence on the e-p scattering results. The analysis also demonstrated the precision with which these effects could be studied and offered new, improved values of the $G_E^p$ form factor not accessible in the original work. Furthermore, by studying the slopes of the measured radiative tails relative to the simulated ones, an alternative approach for the extraction of the proton charge radius was developed, which yielded a new best value for the proton charge radius that could be extracted from the ISR data. The new result, see “Cross-section study” point in Fig. 6, is consistent with the value obtained from the original form factor analysis, but is almost three times as precise as the first result [11].

Fig. 6

The proton charge radius extracted from the electron scattering experiments. The red circles show the results of the ISR experiment. The final radius was determined by analysing the slopes of the measured cross-sections relative to the simulated ones. The value is consistent with the one calculated from the fit of the form factors. Black squares represent the results of previous electron scattering measurements [5, 7, 8, 11, 19,20,21,22,23,24,25,26]. The value obtained from the Lamb shift measurements in muonic hydrogen is shown by the blue line for comparison

Appendices

Appendix A: Systematic uncertainties

Table 1 The relative systematic uncertainties contributing to the uncertainty of the cross-section ratios determined by the ISR experiment

The uncertainties of the cross-section ratios and deduced form factors are dominated by the combination of the experimental uncertainties, presented in Sect. 3, and the uncertainties of the simulation employed to calculate the radiative tail of the elastic scattering process. These need to be studied carefully in order to extract credible results, since some parts depend strongly on the energy of the scattered electron, see Fig. 7. The obtained uncertainties are gathered in Table 1 and discussed in this section.

Fig. 7

Momentum-dependent uncertainty contributions to the cross-section ratios introduced by different effective corrections to the simulation for the $495\,\mathrm {MeV}$ energy setting. The largest contributions to the uncertainty are related to the description of the second-order real photon emission (dashed green line), external radiative corrections (dash-dotted violet line) and the description of pion electroproduction (double-dotted cyan line). The latter is relevant only above the pion production threshold at momenta below $360\,\mathrm {MeV/c}$. The full red line shows the total systematic uncertainty of the extracted cross-section ratios, including experimental uncertainties presented in Sect. 3

The simulation exactly calculates the coherent sum of the amplitudes for the leading diagrams shown in Fig. 1. The next-order vacuum polarization diagrams (with electrons inside the fermion loop) are exactly calculable and represent as a multiplicative factor to the cross section. The uncertainty of this correction is given by the size of the omitted vacuum polarization due to muon loops and is smaller than $0.2\,\%$. The virtual corrections to the Bethe-Heitler diagrams (self-energy corrections and various vertex corrections) require integration of the loop diagrams and are considered as effective corrections to the cross section, using calculations of Ref. [12]. These are accurate to about $1\,\%$, which in turn corresponds to an error of the cross-section ratios smaller than $0.016\,\mathrm {\%}$.

The non-virtual second-order correction (emission of two real photons) is approximated by the corrections to the elastic cross section [12, 27]. Relying on the soft-photon peaking approximation the contribution of this correction to the final uncertainty was estimated from the size of the next-order correction and determined to be smaller than $0.5\,\%$. Hadronic corrections are also considered in the elastic limit using the calculations of Ref. [27]. They contribute only up to $0.5\,\mathrm {\%}$ to the cross section at lowest energies. In the simulation the proton is always on-shell. Hence, the uncertainty of hadronic corrections arises from the part that is related to the internal structure of the proton, described by the generallized polarisabilities [28]. These effects are tiny at our values of $Q^2$, and hadronic corrections contribute less than $\le 5\cdot 10^{-4}\,\%$ to the measured cross-sections. Far away from the elastic peak, one also needs to consider $\mathrm {H}(e,e')n\pi ^{+}$ and $\mathrm {H}(e,e')p\pi ^{0}$ reactions, which contribute up to $10\,\mathrm {\%}$ of all events. These processes were simulated using the MAID model [29] and subtracted from the data. The relative uncertainty of the MAID calculations was estimated to be $5\,\mathrm {\%}$, and is significant only for the $495\,\mathrm {MeV}$ setting, where it contributes $0.5\,{\%}$ to the uncertainty of the measured ratios.

The last important contribution to the systematic uncertainty can be traced back to the formalism of Mo and Tsai [14], employed to describe external corrections to the cross-section, see Sect. 2. These corrections add up to $0.24\,\%$ to the total uncertainty of the measured cross-section ratios.

The obtained uncertainties determine the errors of the deduced form factors discussed in Sect. 5. In the approximation of small $Q^2$ these are linearly proportional to the uncertainties of the cross-section ratios, where the proportionality factor, $(1+ \sigma _{\mathrm {BH-f}}/\sigma _{\mathrm {BH-i}})/2$, depends only on the ratio of the initial-state and final-state radiation parts of the cross-section, $\sigma _{\mathrm {BH-i}}/ \sigma _{\mathrm {BH-f}}$, and approximately equals 5/4.

Table 2 The proton charge form factors obtained with the ISR experiment at three beam energies

Appendix B: Proton charge form factors

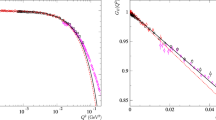
Table 2 collects the proton charge form factors determined by the Initial-State Radiation experiment for $0.001 \le Q^2 \le 0.017\,\mathrm {GeV}^2/c^2$. The results were obtained by studying the reaction $\mathrm {H}(\mathrm {e},\mathrm {e'})\mathrm {p}\gamma$ and comparing the shape of the measured radiative tail with the simulation, using the approach explained in Ref. [11]. The extracted values, presented in the third and fourth column, were then compared to the polynomial Eq. 2. The three data sets were fit with a common parameter for the radius, $r_p$, but with different renormalisation factors, $n_{E_0}$, for each energy, disregarding the original normalisations of the data, determined from the analysis of cross-sections. The analysis considered both statistical and systematic uncertainty of the extracted values of $G_E^p$. In terms of this fit with 21 degrees of freedom and $\chi ^2$ of 18.3, the normalisations and the radius were determined to be:

$$\begin{aligned} n_{195}= & {} 1.000 \pm 0.001_{\mathrm {stat}} \pm 0.003_{\mathrm {syst}}\,,\\ n_{330}= & {} 0.999 \pm 0.001_{\mathrm {stat}} \pm 0.003_{\mathrm {syst}}\,,\\ n_{495}= & {} 1.000 \pm 0.002_{\mathrm {stat}} \pm 0.007_{\mathrm {syst}}\,,\\ r_p= & {} (0.873 \pm 0.017_{\mathrm {stat.}} \pm 0.059_{\mathrm {syst.}} \pm 0.003_\mathrm {mod.})\,\mathrm {fm}\,. \end{aligned}$$

The obtained normalisation parameters were applied to renormalise the experimentally determined form factors in order to match the values of the three energy settings and to ensure consistency of the results with the statical limit $G_E^p(0) = 1$. The corrected values of $G_E^p$ with the corresponding statistical uncertainties are model dependent and are gathered in the fifth and sixth columns of the table. They are also presented in Fig. 8.

Fig. 8

The proton electric form factor as a function of $Q^2$. Empty black points show previous data [7, 22, 24, 30]. The results of this experiment are shown with full red circles. The error bars show statistical uncertainties. Grey structures at the bottom shows the systematic uncertainties for the three energy settings. The curve corresponds to a polynomial fit to the data defined by Eq. (2). The blue error band around the fit shows its uncertainty, caused by the statistical and systematic uncertainties of the data. The magenta line with the corresponding error band demonstrates the best $G_{\mathrm {E}}^{p}$ model, determined by the new method, presented in Sect. 6