1 Introduction

The standard way to estimate tsunami inundation maps is to apply numerical nonlinear shallow water (NLSW) models that include drying-wetting schemes (Titov and Gonzalez 1997; LeVeque and George 2008; Løvholt et al. 2010; Dutykh et al. 2011; de la Asunción et al. 2013; Wronna et al. 2015; Macías et al. 2017). However, if the inundation needs to be quantified over large coastal stretches (e.g. country scale or larger), NLSW inundation simulations are most often not feasible. This is due either to the large computational cost or to the lack of required high-resolution topo-bathymetric models. This issue is particularly relevant for probabilistic tsunami hazard analysis (PTHA, Geist and Parsons 2006; Grezio et al. 2017), in which a large number of scenario simulations must be carried out to take into account the natural potential variability of the tsunami sources (e.g., Selva et al. 2016). Intermediate methods can limit the number of scenario simulations for local PTHA (Gonzalez et al. 2009; Lorito et al. 2015), but they still require high-resolution coastal bathymetric and topographical data that are typically not available over large geographical scales. We still need simpler methods for estimating tsunami inundation heights in PTHA, particularly over large regions.

A faster, yet more approximate, method than NLSW is to relate the nearshore surface elevation to the water elevation at the shoreline, which then acts as an approximation for the maximum inundation height (MIH). We refer to this method as the amplification factor (AF) method. Combined with results from offshore tsunami simulations, AF methods can be used to estimate the tsunami maximum inundation height at a coastal location.

The first version of the AF method (Løvholt et al. 2012, 2015) considered a set of only a few amplification factors based on idealized and overly simplified bathymetric profiles. The idea was that, in principle, these could be fitted to a coastline at any given place. A related AF model that also enables a fast calculation of tsunami heights for tsunami early warning was recently developed by Gailler et al. (2018). In contrast to the method of Løvholt et al. (2012), which is the basis for the model in this paper, the method developed by Gailler et al. (2018) needs to be calibrated with detailed bathymetric/topographic information and with high-resolution NLSW simulations for each site where it is applied.

For practical purposes, and due to a lack of alternatives, the application of Green’s law amplification to a given reference water depth (often 0.5 m) has previously been employed to estimate tsunami inundation heights from offshore points as an alternative to the AF method (Sørensen et al. 2012; Brizuela et al. 2014; Horspool et al. 2014; Hébert and Schindelé 2015). However, as pointed out by Hébert and Schindelé (2015) and Davies et al. (2018), the choice of the reference water depth in Green’s law makes the method subjective. In this paper, it will be demonstrated that the AF method represents a more accurate method for estimating the coastal amplification than Green’s law, because local factors influencing the run-up, such as local bathymetry, wave polarity, and wave length, enable a more accurate approach. In addition, a series of new facilities, which will be described in a moment, makes the new AF method more suitable for use in regional PTHA than other previous approximate methods.

The AF method developed here has several new characteristics. Rather than using a predefined set of idealized bathymetric profiles, our method employs cross-sections from actual local bathymetry. The amplified height (AH) at the shoreline (see Fig. 1) is then quantified with a linear shallow water (LSW) model along a 1D profile close to orthogonal to the shoreline, much like the previous AF method. For a specific point on the coastline, the AH acts as a proxy for the MIH. As discussed by Løvholt et al. (2012), the AF method gives exact estimates for the MIH even under the special condition of plane non-breaking waves. Consequently, as will be demonstrated in this paper, the AH is rather a good estimator of the median of the whole MIH distribution along a set of onshore transects, over a coastline stretch of, say, a few kilometers. On the other hand, the AF method is designed to operate over large stretches of coastline, and the spatial resolution is much coarser than in numerical tsunami inundation models. Moreover, local phenomena such as wave focusing and refraction usually give rise to significant local variability in the MIH that cannot be captured by the AF method, which assumes plane wave amplification. As shown in the lower panel in Fig. 1, there is typically significant alongshore coastal variability in MIH. It was therefore necessary to upgrade the AF method to capture this inundation height variability as a model uncertainty.

Fig. 1
figure 1

Upper panel: Sketch exemplifying the amplified height (AH) obtained from the amplification factor method as well as the maximum inundation height (MIH) obtained from a reference model over a local transect. The MIH represents the reference value, whereas the AH is a proxy for the MIH. The dashed red curve is the envelope of the amplified wave signal using the AF method (we denote the height at the shoreline AH). The yellow curve shows the corresponding maximum envelope of the coastal amplitude (offshore) and the inundation height (onshore) obtained from an NLSW reference model, and we denote the maximum in this curve MIH. The vertical value where the inundation height intersects the topography is the run-up height, and the corresponding horizontal distance is the inundation distance. Lower panel: example of a coastal distribution of the MIH derived from the 2HD (depth-averaged 2D model) reference model, drawn together with the single AH value derived for a single transect available for this coastal stretch

Full size image

Previous attempts to quantify AF-related tsunami inundation height uncertainty and bias are limited to a few studies (Davies et al. 2018, and references therein). Davies et al. (2018) estimated the AF uncertainty and bias by comparing offshore tsunami simulations combined with AF analysis against observed run-up for four tsunamigenic earthquakes (Chile, 1960; Alaska, 1964; Indian Ocean, 2004; Tohoku, 2011) using the previous AF version based on idealized and much simplified bathymetric transects. The authors found that tsunami simulations combined with the AF gave a relatively small bias compared to observed run-up heights, whereas a large log-normal root mean square (\(\sigma \sim 0.9\)) was found. However, their analysis merged uncertainty from the source with the one associated with the AF method. Therefore, their uncertainties combined the variability due to tsunami source complexity (e.g., heterogeneous coseismic slip or other simplifications in seismic source and tsunami generation) and propagation modeling, and possibly even other sources such as landslides, in addition to the inherent variability in the inundation process we try to quantify here. Thus, their variability due to the inundation process was not separated from the variability due to the source and tsunami propagation. In this study, we quantify the uncertainty of the inundation process separately by employing detailed high-resolution inundation simulations, tying the observed uncertainties from the inundation simulations directly to the AF method.

This paper is organized as follows: Section 2 describes the computation of the local amplification factors. In Sect. 3, we describe the inundation simulations for six different test sites in southern Europe. In Sect. 4, we estimate and analyze the bias and uncertainty of the method by comparing the AF performance at the test sites with the NLSW inundation models. In Sect. 5, we demonstrate with an example how the results can be used in a PTHA developed for production of tsunami hazard maps in the North-Eastern Atlantic, Mediterranean and connected seas (NEAM) region.

2 Amplification Factors Based on Local Bathymetric Transects

2.1 New Amplification Factors Derived from Transect Simulations

Løvholt et al. (2012) used a very limited set of idealized bilinear profiles as a basis for the AF computations. In the present study, instead, transects of the coastal water depth were extracted directly from the local bathymetry in the Mediterranean Sea, the Black Sea, and the North-Eastern Atlantic (see Fig. 2). The procedure for extracting these local transects is explained in Appendix 1. Following Løvholt et al. (2012), a 1D LSW model, solved over a staggered Arakawa C-grid with variable spacing, is used for the AF production runs. The resolution of the grid depends on the wave period and the water depth and is tuned to give a constant Courant number Cr = 0.9 over the entire domain. The Courant number is here defined as

$$\begin{aligned} Cr=\frac{\sqrt{gh}\Delta t}{\Delta x} \end{aligned}$$
(1)

where h is the local water depth, \(\Delta x\) is horizontal grid resolution, and \(\varDelta t\) the time step.

For waves with a period larger than 600 s, the grid size ranges from about 300 m in the deepest part of the domain (water depth of 2000 m) down to 7 m at 1 m depth; for a wave period shorter than 300 s, the grid resolution varies from 80 m to about 2 m, respectively. The grid spacing is not further refined in water depths less than 1 m. The resolution applied in the simulations is justified by convergence tests. At the shoreline we have applied a no-flux boundary condition, and the waves are fed into the model from the offshore boundary.

Fig. 2
figure 2

Map showing all profiles applied in the study

Full size image

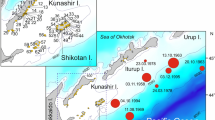
The new method for computing the amplification factors starts with defining the AF points of interest (POIs). The POIs are located at longitude-latitude coordinates inside the computational domain employed for the 2HD tsunami propagation simulations. In this study, amplification factors are computed for almost evenly spaced POIs located every 20 km along the shoreline. For each POI along the 50 m isobath, about 40 depth profiles (exemplified in the upper panels of Figs. 3, 4, 5) are extracted approximately normal to the shoreline, each with a distance of 1 km apart, as described in Appendix 1. However, in the case of complex coastal geometries, deviation from the normal incidence may take place.

The amplification factors are computed along seven subjectively selected profiles out of the 40 profiles. The subjective selection was made to enable computational feasibility. An initial wave of 1 m height in deep water, shaped as a single-period sinusoidal wave pulse (N-shaped wave), is fed over the deep water boundary of the model (see Fig. 1). Linear shallow water (LSW) simulations were carried out for all profiles, both for leading trough or leading peak and for a set of wave periods (120, 300, 600, 1000, 1800, and 3600 s).

Maximum surface elevations from the LSW simulation at 50 m depth and at the shoreline (0 m depth) are extracted. For each profile, we compute the amplification factor, which is defined as the ratio of the height between the latter and the former (i.e. \(A_1\) and \(A_2\) in the upper panel of Fig. 1). We use the median value of the seven amplification factors to avoid unrealistic alongshore fluctuations. Examples of amplification factors and related median values as a function of the incident wave periods are shown in the lower panels of Figs. 3, 4, 5. AF values for all combinations of wave polarities and wave periods are stored in lookup tables. As an example, amplification factors for a leading trough polarity and wave period of 600 s for the Mediterranean and Black Sea are depicted in Fig. 6.

Two versions of the factors were produced, one set using the raw amplification factor values and one set of factors smoothed along the shoreline with a median filter (using a filter length of five points). The median filtering was performed as an additional measure to avoid artificially short amplification fluctuations along the shoreline (see example for the Black Sea in Fig. 7).

Fig. 3
figure 3

Example of depth profiles (top) and amplification factors (bottom) representing the hazard point 405 (at Sines, Portugal). The amplification factors are shown for the seven depth profiles as explained in the text, versus the wave period (seconds). The red and blue curves are factors for leading peak and leading trough, respectively. The thin curves are the factors for the seven local profiles, while the thick lines are the median values for leading peak and leading trough at this location

Full size image
Fig. 4
figure 4

Example of depth profiles and amplification factors representing the hazard point 7465 (at Heraklion, Greece). See also caption in Fig. 3

Full size image
Fig. 5
figure 5

Example of depth profiles and amplification factors representing the hazard point 10746 (at Sant Jordi, Mallorca). See also caption in Fig. 3

Full size image
Fig. 6
figure 6

The amplification factors for the Mediterranean and Black Seas for the case with a leading trough and a wave period of 600 s. The factors are filtered along the shoreline with a median filter as explained in the text

Full size image
Fig. 7
figure 7

The amplification factors for Black Sea as function of the hazard points lying along the shoreline (ID numbers). The figure shows the effect of filtering the factors along the shoreline. The labels “neg” and “pos” relate to leading trough and leading peak, respectively. The tag “-sm” indicates filtered values (median filter), as explained in the text

Full size image

As expected, we do observe that the shorter waves and waves with leading trough are amplified more than the longer waves and waves with a leading peak (Figs. 3, 4, 5, lower panels). We also observe that the amplification factors decrease as the period increases; in some cases the behavior appears different and the amplification factors are locally higher with respect to lower periods such as in Fig. 5 (see around period of 1000 s). This stems from interference between incident and reflected waves in the linear shallow water simulations: when the travel time from the POI to the shoreline and back to the POI for the leading trough matches the arrival of the trailing peak here, the measured wave height at the POI is low (trough is canceling the peak) and the amplification factor is high.

3 Local Inundation Simulations for Bias and Uncertainty Estimation

In order to evaluate uncertainties of the method of amplification factors, we systematically compare its results against direct NLSW inundation simulations. The employed NLSW model (Tsunami-HySEA, de la Asunción et al. 2013; Macías et al. 2017) is properly benchmarked, and is hence a suitable reference model towards the less accurate AF method. Still, a limitation with this approach is that the inundation simulations are not compared directly to field observations.

Fig. 8
figure 8

Location map showing the six test sites (dots) used for local inundation simulations and the epicenters of the earthquake scenarios (stars). The insets show the topo-bathymetric nested grids used for each test site in the simulations

Full size image

Comparisons between the AF and the NLSW models are undertaken at the six test sites for which a suitable and sufficiently detailed DEM existed. The test sites include one in the Atlantic Ocean, namely Sines, Portugal, with the remainder in the Mediterranean: Colonia Sant Jordi (Mallorca) and SE Iberia in Spain, Siracusa and the Catania plain in Italy, and Heraklion on the island of Crete in Greece (Fig. 8). For each test site, we use 96 earthquake sources with varying magnitude, strike, dip, and rake in order to explore a variety of situations as far as the source mechanism is concerned and, as a consequence, the wave period and wave polarity variability. In particular, we use six different moment magnitudes (7.1, 7.5, 8.1, 8.5, 8.8, 9.0), four strike angles (22.5, 112.5, 202.5, 292.5), and four pairs of dip/rake angles (10/90, 30/90, 50/270, 70/270). Empirical earthquake scaling laws (Strasser et al. 2010) are then employed to define the fault size (length and width) for each earthquake source. The average slip (D) for each scenario is established by considering the classical relationship \(M = \mu AD\), where M is the seismic moment, \(\mu \) is the shear modulus (30 GPa), and A is the rupture area of the seismic source.

We use the NLSW Tsunami-HySEA numerical code (see, e.g., de la Asunción et al. 2013; Macías et al. 2017) to simulate the distribution of the tsunami inundation height over the extent of the different sites. All offshore tsunami simulations are conducted on regular grids with a spatial resolution of 30 arc-sec. The NLSW models additionally use nested grids to simulate detailed local inundation at test sites. The resolution of the finest grid is about 10 m at all locations. The Manning-friction (n) is set to \(n=0.03\) in all simulations. We note that while \(n=0.03\) is typically a friction value for overland flow (e.g. Kaiser et al. 2011), this value will be site-dependent and vary spatially as well, and hence using a constant value represents a simplification.

For each test site and source scenario we apply the new AF method to quantify MIHs. As prescribed by the method, MIH is quantified by multiplying the maximum offshore surface elevation retrieved at the POI, taking wave characteristics retrieved from time series at the POI, with specific AF retrieved from the relevant lookup table. The method for selecting the maximum offshore surface elevations and related wave periods and polarities at the POI are described in Appendix 2.

4 Maximum Inundation Height Uncertainty and Bias

As explained in Sect. 3, the comparison between the AF method and corresponding NLSW simulations is made from six locations, each site subject to about 96 earthquake-induced tsunami scenario simulations. The new AFs depend on the coastal slope configuration, the tsunami wave period, and the tsunami wave polarity, as simulated in a single POI located offshore along the 50 m isobath. As the AFs are based on a linear method, they are amplitude-independent. For each scenario, we extracted the largest MIHs from the NLSW simulations for a given coastline location. MIH maxima were extracted in either the north–south or east–west direction, line by line, for each grid cell along the preferred coordinate axis. That is, if the shoreline is oriented mostly east–west for a given site, we search along lines oriented in the north–south direction, while if the shoreline is predominantly oriented more north–south for another site, we search along lines oriented in the east–west direction. In some special cases, the height of the terrain landside of the shoreline is too high and too steep to be inundated. In these situations, we also include values of maximum surface elevation for a small distance seaside from the shoreline (at least one cell away).

From counting all MIHs over the computational domain (NLSW) at each test site, we obtain an MIH empirical probability density function (ePDF) for each simulation. Each MIH ePDF is then fitted to a log-normal probability density function (PDF), using standard fitting tools in Matlab. We note that the log-normal PDF implies a normal distribution of the natural logarithm of the random variable with median \(\text {e}^\mu \) and variance \(\sigma ^2\), in this case representing the MIH. The log-normal distribution of the MIH reads:

$$\begin{aligned} p(\text {MIH})=\frac{1}{\sqrt{2\pi } \text {MIH} \sigma }\exp {-\left( \frac{(\ln \text {MIH} - \mu )^2}{2\sigma ^2} \right) } \end{aligned}$$
(2)
Fig. 9
figure 9

Distribution of MIHs from three individual NLSW simulations, including median values from each distribution and the related AH. Upper panel, MIH distribution in Catania due to a \(M_w\) 8.5 earthquake. Middle panel, MIH distribution in Heraklion due to a \(M_w\) 7.5 earthquake. Lower panel, MIH distribution in SE Iberia due to a \(M_w\) 7.1 earthquake

Full size image

We stress that the log-normal median value of the MIH over the computational domain for the NLSW simulation is \(\mathrm {e}^\mu \). These fitted medians, arising from each NLSW simulation, are compared with amplified heights (\(A\times \eta \), where A is the amplification factor and \(\eta \) is the height offshore) resulting from the AF method, in order to quantify biases for the individual simulations (and later on bias distribution). To this end, we define the normalized bias

$$\begin{aligned} \epsilon =\frac{(A\times \eta )-\mathrm {e}^\mu }{\mathrm {e}^\mu }, \end{aligned}$$
(3)

to quantify the MIH bias due to the AF method towards the more accurate NLSW model for each model run and site. Examples of PDF for three individual model runs for the Catania, Heraklion, and SE Iberia sites are shown in Fig. 9. As demonstrated, the MIH distributions can be quite heterogeneous in terms of both their shape and/or their widths. To this end, we performed a Kolmogorov–Smirnov test (Massey 1951) (using the logarithm of the MIH as the density variable) to investigate the validity of the fit of each empirical distribution towards a log-normal distribution. Below, we refer to this as the KS test. Using the KS test, we found that just \(7\%\) of the distributions from individual model runs had p values higher than \(1\%\) (i.e. more than \(1\%\) probability of exhibiting a log-normal distribution). Some sites, in particular Colonia Sant Jordi, had higher representation of statistically significant log-normal fits than other sites. We speculate that heterogeneous spatial characteristics in some of the other sites have given rise to different mean MIH in different parts of the domain, implying that these sites are not easily fitted into one single distribution. This deserves to be better investigated. Nonetheless, the median MIHs from the NLSW simulations have values close to the simplified AHs in the present examples.

Fig. 10
figure 10

Distribution of median MIHs from the NLSW simulations compared to all the corresponding AHs

Full size image

4.1 Inundation Height Statistics for the Full Parameter Set

A first impression of the overall results can be drawn by inspecting Fig. 10, showing a histogram of all the median MIHs derived by the NLSW simulations compared with respective AHs. This figure shows that while overall distributions are comparable for the two models, there seems to be a weak tendency for median MIH values from NLSW simulations to exceed the AHs.

Fig. 11
figure 11

Normalized bias: upper panel, using amplification factors; lower panel, using Green’s law

Full size image

To gain a deeper and more quantitative insight, we carried out a statistical analysis based on the MIH PDFs, biases, and log-normal uncertainties. In the statistical analysis, both the merged results and statistics isolating the effects of different factors were analyzed.

The distribution of the normalized AF bias for all model simulations at all sites is shown in the upper panel of Fig. 11. The individual biases are close to being normally distributed, and the KS test returned a p value of \(41\%\). The mean bias is \(\bar{\epsilon }_{AF}\)= −5%, which indicates that the AH is slightly lower than the median MIH predicted by the NLSW model. This is in contrast to the first version of the AF method (Løvholt et al. 2012), for which a positive bias was quantified, though against observations rather than simulations (Davies et al. 2018), as already noted. Figure 11 further shows that the standard deviation of the normalized AF bias is \(\sigma _{AF}\,=\) 0.28. Similarly, we computed the normalized bias using Green’s law amplification to a reference depth of 0.5 m. As shown in the lower panel of Fig. 11, Green’s law applied to this reference depth provides a strong positive bias of \(\bar{\epsilon }_ {Green}\) = 18%, meaning that Green’s law would strongly overestimate the inundation height predicted by the NLSW reference model. Furthermore, the Green’s law biases are associated with a significantly larger uncertainty (\(\sigma_{\text \it{Green}}\) = 0.46). The Green’s law biases are moreover more strongly skewed than AF biases and definitely not normally distributed according to the KS test. This difference may reflect, among other things, the reference depth subjectivity that is not present in the AF method.

Fig. 12
figure 12

Distribution of the variability from all model runs

Full size image

The bias from various model runs represents just one component of the variability. In addition to the variability of the bias, as shown in Fig. 9, the tsunami inundation height does vary spatially across each site. This variability is related only to the properties of the NLSW simulations at the site, and not to the AF method as such. However, when applying the AF method, we must take this uncertainty into account. For the examples shown in Fig. 9, we obtain log-normal standard deviations \(\sigma \) of 0.26, 0.43, and 0.23, respectively. The distribution of all the \(\sigma \) values is shown in Fig. 12, displaying a mean value of \(\bar{\sigma }\) = 0.25 and standard error of \(\sigma _\sigma \) = 0.41. By visual inspection, the distribution of local standard deviations seems to follow a log-normal distribution relatively closely, despite the data displaying a more peaky behavior than the fitted log-normal PDF. It is worth noting that of the three sources of uncertainty contributing to the AF (bias uncertainty \(\sigma _\epsilon \), mean local uncertainty \(\bar{\sigma }\), and standard error \(\sigma _\sigma \)), the standard error \(\sigma _\sigma \) is the largest contributor. In this study, \(\sigma _\sigma \) reflects the variability owing to different sites, tsunami sources, wave polarity, wave period, etc. In the next subsection, we will demonstrate with examples how bias and variability differ.

Taking the root mean sum of the different \(\sigma \)’s (\(\sigma _\epsilon \) = 0.28, \(\bar{\sigma }\) = 0.25, and \(\sigma _\sigma \) = 0.41) for the full parameter set simulations, we arrive at a root mean square sum of 0.55 due to the inundation process. It is noted that Davies et al. (2018) found an overall uncertainty of 0.92 when comparing PTHA results with observations from past events. If the uncertainty found in this paper is representative for the inundation process, the overall uncertainty of 0.92 in Davies et al. (2018) would be the sum of the inundation uncertainty and a residual uncertainty due to other sources. By removing the inundation uncertainty from the uncertainty obtained by Davies et al. (2018), we obtain a residual uncertainty of 0.73, from which we may speculate that the variability due to the inundation would then contribute to just less than half of the total uncertainty found by Davies et al. (2018). In this context, we note that Geist (2002) reports coefficients of variation in the range of 0.25–0.35 due to variable slip, which is thought to be one of the governing factors in inundation height uncertainty. These aspects deserves to be better investigated. On the other hand, Davies et al. (2018) used idealized AF profiles, which are most likely have a larger overall bias due to a more crude bathymetric representation. In any case, the present analysis shows that the variability in inundation is a strong overall component in the inundation height uncertainty, which needs to be accounted for in a regional PTHA method.

4.2 Inundation Height Statistics for Parameter Subsets

The bias and variability are further examined by carrying out the statistics for certain sets of parameters (e.g. only for positive wave polarity, only for short-period waves, for an individual site).

First, we examine the bias and local MIH variability separately for the two wave polarities (leading trough and leading peak). The statistical distributions for the two different polarities are quite similar to those shown in Figs. 11 and 12, and hence we choose not to display them. We also note that the p values of the bias distributions are 91 \(\%\) and 14 \(\%\), respectively. However, the small to moderate average biases (3% for leading trough and 8% for leading peak) suggest that the distinction between leading trough and leading peak was necessary. Such a distinction cannot be made with simpler methods such as Green’s law amplification.

Fig. 13
figure 13

Normalized bias distributions for different ranges of the wave period obtained from offshore tsunami simulations. Upper panel, short wave periods (\(T \le 600\) s); Middle panel, intermediate wave periods (600 s \(< T \le 1800\) s); Lower panel, long wave periods (\(T > 1800\) s)

Full size image

Second, we examine the bias by making statistics for different ranges of incident wave periods T from the offshore tsunami simulations, that is \(T \le 600\) s, 600 s\(<T \le 1800\) s, and 1800 s \(< T\). The bias distributions are all normally distributed, with p values from KS tests ranging from 53 \(\%\) to 84 \(\%\). The bias distributions in Fig. 13 show that the shortest wave periods display a positive bias (AH overestimation), and the intermediate wave periods a small negative bias (AH underestimation), whereas for the longest wave periods a strong negative bias is observed (AH underestimation). The strong bias for the longest wave periods may be due to several factors. Determining the causes for these offsets should be subject to further investigation. However, we assume that the limited number of wave periods covered by the AF look-up tables can provide biases for instances when an input wave period from a tsunami simulation is pronouncedly different from the ones in the look-up table. Further, the filtering and zero-crossing techniques sometimes introduce wave lengths that are too large, which reduces inundation heights in the AF method. We also see that the largest bias variability is observed for the shortest and longest wave periods. However, the largest fraction of simulations are located in the intermediate regime.

Fig. 14
figure 14

Bias and variability for three different sites. Left panels, model bias. Right panels, model variability. Upper panels, Catania site. Middle panels, Heraklion site. Lower panels, SE Iberia site

Full size image

Third, we examine the bias and local variability for three sites (Catania, Heraklion, and SE Iberia) in Fig. 14. Strong negative average biases (AH underestimation) are shown for Catania and Heraklion, whereas a slight positive bias (AH overestimation) is shown for SE Iberia. We further see that the three sites have pronouncedly different spreads with respect to both the bias and local variability, with the Heraklion site being clearly more heterogeneous, and SE Iberia the site with the smallest variability. This is also reflected in the p values from the KS tests using the bias distributions as input, giving lowest values for Heraklion (\(1\%\)) and highest values for SE Iberia (\(61\%\)). It is noted that from a practical point of view, separating the variability and bias from different locations is not feasible, as we cannot perform NLSW simulations at all relevant locations. Consequently, merging uncertainties from different sites would increase the overall MIH uncertainty in a PTHA analysis.

5 Uncertainty Treatment in PTHA

Summarizing from previous sections, the AF depends on both the characteristics of local bathymetry (coastal slope configuration) and the characteristics of the tsunami scenario (dominant period and polarity), as simulated in a single POI located offshore. Multiplying the AF to the tsunami simulated in this POI, we obtain an approximate median MIH for the nearby coast due to the considered individual tsunami scenario.

For the i-th tsunami scenario in the j-th POI, we indicate the maximum offshore elevation at the POI and the corresponding MIH value with \(\eta _{ij}\) and \(\text {MIH}_{ij}\), respectively. \(\text {MIH}_{ij}\) corresponds, after correction for a generally quite small bias, to the median value of the distribution of MIH values that the i-th tsunami scenario causes in stripes of land perpendicular to the coast and located around the projection to the coast and inland of the j-th POI.

In fact, as demonstrated by the NLSW simulations, this distribution can be approximated by a log-normal distribution for MIH, with a median that is well approximated by \(MIH_{ij}\) and a reasonably small \(\sigma \) (the standard deviation of the natural logarithm of MIH). These parameters are different for different scenarios and POIs. In particular, for the i-th tsunami scenario \(\eta _{ij}\) at the j-th POI, we indicated these parameters with \(\mu _{ij}\) and \(\sigma _{ij}\), and, considering the AF \(A_{ij}\) and the normalized bias \(\epsilon _{ij}\) (compare Eq. (2)), we have \(\mu _{ij}=\) ln\((A_{ij}\)\(\eta _{ij}\)/(1+ \(\epsilon _{ij}\))). Among these parameters, the AF \(A_{ij}\) and \(\eta _{ij}\) depend on both the coastal slope around the POI and the tsunami scenario. Instead, the parameters \(\sigma _{ij}\) and \(\epsilon _{ij}\) depend primarily on the local coastal configuration around the j-th POI and can be estimated only with an NLSW simulation of the i-th tsunami scenario in the j-th location.

For the purpose of PTHA, a large number of POIs are defined, each POI uniquely representing an entire stretch of the nearby coastline. Assuming that this coast is reasonably close to the POI, we may assume that, for each tsunami scenario, the MIH distribution on this coast is again well represented by a log-normal distribution. Given one randomly selected coastal point represented by the j-th POI, the probability that a given MIH value is exceeded due to the i-th tsunami scenario in the stripe to which this point belongs, can be computed from this log-normal distribution, that is:

$$\begin{aligned} Pr_{ij}(> \text {MIH}|\text {MIH}_{ij})=1-\varPhi \left( \frac{\ln {\text {MIH}}-\ln {\mu _{ij}}}{\sigma _{ij}}\right) =1-\varPhi \left( \frac{\ln {\text {MIH}}-\ln {(A_{ij}\eta _{ij}/(1+\epsilon _{ij}))}}{\sigma _{ij}}\right) , \end{aligned}$$
(4)

where \(\varPhi (.)\) indicates the cumulative distribution function of a normal distribution.

This curve can be interpreted as the hazard curve for the hazard intensity MIH of one randomly selected point within the stretch of coastline near the j-th POI, conditional to the occurrence of the i-th tsunami scenario with best guess \(\text {MIH} = \text {MIH}_{ij} = A_{ij} \eta _{ij} /(1+ \epsilon _{ij}\)).

There is, however, a certain degree of epistemic uncertainty regarding the parameters of this equation. Indeed, all these parameters are reasonably well known only for the locations in which we have the NLSW simulations. In fact, the computational cost for achieving this for all POIs of a regional hazard quantification is typically unaffordable, since they are a very large number, and moreover precise local topographic/bathymetric data are usually not available. The parameters \(A_{ij}\), \(\mu _{ij}\), \(\epsilon _{ij}\), and \(\sigma _{ij}\) must then be estimated from the available general information. More specifically:

  • \(A_{ij}\) for a set of different tsunami scenarios has been extracted as shown in previous sections.

  • The time history of the tsunami and the local \(\eta _{ij}\) may be estimated from linear simulations of the propagation in deep sea of each individual tsunami scenario.

  • In regional PTHA, these simulations are barely affordable; therefore, both tsunami time history and \(\eta _{ij}\) are here approximated as a linear combination of unit sources (Molinari et al. 2016). Here we introduce \(z_{ij}\) as a further source of epistemic uncertainty, which is introduced by combining unit sources rather than simulating all of them as a single source. The treatment of this uncertainty is elaborated below.

  • For the estimation of the parameters \(\epsilon _{ij}\) and \(\sigma _{ij}\), we assume that combining all the information from selected test sites reasonably approximates the variability of these parameters for all the POIs.

To propagate this epistemic uncertainty for the i-th tsunami scenario at the j-th POI, we adopt a Monte Carlo simulation scheme. We take as input the applicable \(A_{ij}\) and \(z_{ij}\) obtained from the simulation of the i-th tsunami scenario based on unit source combination for the j-th POI. Then, for each POI and each tsunami scenario, we sample:

  • The correction \(\delta ^*\) from the empirical distribution \(\delta =(z-\eta )/\eta \). This is the distribution of the relative error of the approximated \(\eta \) values due to the use of unit sources (as defined in Molinari et al. (2016), see their Figure 4d). This distribution is obtained by aggregation of a very large number of NLSW simulations with variable source and site, over a quite large range of tsunami intensities (up to \(> 10\,m\)), and we may assume that they reasonably approximate this uncertainty source for PTHA purposes.

  • The parameters \(\epsilon ^*\) and \(\sigma ^*\) from the empirical distributions of b and \(\sigma \) of Fig. 11, upper panel, and Fig. 12.

To obtain the consequent hazard curve, we can substitute each sampled {\(\delta ^*\),\(\epsilon ^*\),\(\sigma ^*\)} to the corresponding quantities into Eq. (3) as:

$$\begin{aligned} Pr_{ij}(> \text {MIH}|\text {MIH}_{ij})=1-\varPhi \left( \frac{\ln {\text {MIH}}-\ln { ( A_{ij} z_{ij} / ((1+\delta ^*)(1+\epsilon ^*) ))}}{\sigma ^*}\right) ; \end{aligned}$$
(5)

in particular, we set \(\text {MIH}_{ij}\) = \(A_{ij}\)\(z_{ij}\) as the best-guess reference MIH from the modeled i-th scenario in the j-th POI.

Repeating this procedure N (e.g. 1000) times, we obtain N alternative conditional hazard curves, representing the sampled epistemic uncertainty in the conditional hazard. To increase the computational efficiency of this estimation, since {\(\delta ^*\),\(\epsilon ^*\),\(\sigma ^*\)} do not depend on the selected POI or tsunami scenario, they can be pre-computed for a discrete number of possible MIH values, to be subsequently applied to the different scenarios and POIs.

In Fig. 15, we report one example of the obtained epistemic uncertainty for a \(\text {MIH}_{ij}\) value of 5m. In this example, we see that for the mean of the epistemic uncertainty of the model, the frequency of MIH exceeding 5m in one randomly selected point over the coastline is 50%, with resulting wide confidence ranges of \(\sim 15\%\) considering the 16th and 84th percentiles.

Fig. 15
figure 15

Conditional hazard curve for a \(MIH_{ij}\) = 5 m and relative epistemic uncertainty. In gray, we report the N = 1000 sampled alternative curves, while in blue and red we report different statistics of the epistemic uncertainty (blue, mean; red median; dotted red 2nd, 16th, 84th, and 98th percentiles)

Full size image

6 Conclusion

In this paper, a new version of the amplification factor (AF) method for tsunami inundation height estimation has been presented. The new version represents a major upgrade compared to previous AF models, by taking into account the local bathymetry and the uncertainty introduced by using an approximated approach to the inundation process estimation through NLSW models. Because of the new AF capabilities, we can for the first time properly estimate the probability distribution of the maximum inundation height for PTHA. Another step forward is that the resulting MIHs emerging from the model are anchored towards a comprehensive set of more accurate reference models. The new method is implemented for the whole NEAM region, for the purpose of probabilistic tsunami hazard analysis for the TSUMAPS-NEAM project.

The AF method is set up to estimate the median value of the maximum inundation height at an area along the coast, when combined with tsunami propagation models. By linking the AF results with local inundation NLSW simulation results, we have also been able to add the inundation uncertainty into the AF model. Statistical analysis of the different sources of uncertainty is performed through 576 local inundation simulations for different earthquake sources and coastal sites. For example, the quantified bias indicates that the AF method may yield a slight underestimation (5%) of the median inundation height at a given site. However, the AF method yields much more accurate results than the Green’s law method with respect to both a smaller overall bias and reduced uncertainty.

By comparing results from the inundation simulations with the AF results, we find mainly three sources of uncertainty related to employing the AF method, namely variability in positive and negative biases, local variability in the maximum inundation height (owing to the fact that AF is non-local), and the standard error, i.e. the uncertainty of the variability (because different sites and sources produce different inundation variability). Overall, the results show that the inundation variability is strong and needs to be accounted for in a regional PTHA method.

When the inundation statistics is conducted for smaller subsets of the simulation data, for instance for a single site, statistical distributions tend to be rather heterogeneous. When the results are aggregated, more well-defined normal distributions (for the bias) and log-normal distributions (for the local variability) are obtained. Taking into account that the AF method is designed for regional applications, at present state, merging uncertainties from different sites and sources into a single uncertainty seems to be the most robust option, although this increases the overall uncertainty in a hazard estimate. However, by including many more NLSW simulations in the future, for example covering more sites and sources, we would expect to improve run-up estimation capabilities and to reduce related uncertainties, for instance by better taking into account individual bias factors.

Hence, in its present form, the AF method is primarily set up to assist regional hazard quantification, and cannot be used for estimation of maximum run-up heights or as a replacement for local detailed inundation maps. For correct use, both the uncertainty and the bias associated with the method and with the specific hazard metric need to be taken into account.