Modelling the Removal of Gaseous Pollutants and Particulate Matters from the Atmosphere of a City by Rain: Effect of Cloud Density

Abstract

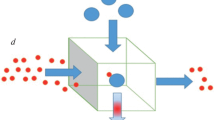
In this paper, an original nonlinear mathematical model for the removal of gaseous pollutants and particulate matters from the atmosphere of an industrial city by rain is proposed and analyzed. It is assumed that five interacting phases in the atmosphere of the city exist, i.e., cloud droplets phase, raindrops phase, gaseous pollutants phase, particulate matters phase, and the phase of absorbed gaseous pollutants in raindrops. It is assumed further that these phases undergo nonlinear interactions in the atmosphere, while gaseous pollutant interacts with cloud droplets as well as with raindrops but particulate matters interact only with raindrops. The gravitational settling and reversible reaction processes have also been considered appropriately in the model. By analyzing the model, it is shown that both the gaseous pollutants and particulate matters may be removed from the atmosphere under certain conditions, provided the rates of formation of cloud droplets and raindrops are sufficiently large. It is noted that under unfavorable atmospheric conditions, rain does not occur and pollutants are not removed from the atmosphere.

Appendices

Appendix A

Proof of the Theorem 1

To establish the local asymptotic stability of E ^*, let us consider the following positive definite function,

$$V = \frac{1}{2}{\left( {k_{0} C^{{\text{2}}}_{{{\text{d}}1}} + k_{1} C^{{\text{2}}}_{{{\text{r1}}}} + k_{2} C^{2}_{1} + k_{3} C^{{\text{2}}}_{{{\text{a1}}}} + k_{4} C^{2}_{{{\text{p1}}}} } \right)}$$

(A1)

where C _d1, C _r1, C ₁, C _a1, and C _p1 are small perturbations from E*, i.e.,

$$ C_{{\text{d}}} = C^{ * }_{{\text{d}}} + C_{{{\text{d1}}}} {\text{,}}\,\,C_{{\text{r}}} = C^{ * }_{{\text{r}}} + C_{{{\text{r1}}}} ,\,\,C = C^{ * } + C_{1} ,\,\,\,C_{{\text{a}}} = C^{ * }_{{\text{a}}} + C_{{{\text{a1}}}} ,\,\,C_{{\text{p}}} = C^{ * }_{{\text{p}}} + C_{{{\text{p1}}}} $$

Differentiating (A1) w.r.t ‘t’ and using the linearized system of Equations (1)–(5) corresponding to E ^*, we get

$$\begin{array}{*{20}l} {{\frac{{dV}}{{dt}} = } \hfill} & {{ - k_{0} {\left( {\lambda _{0} + \lambda _{1} C^{ * } } \right)}C^{2}_{{{\text{d}}1}} - k_{1} \frac{{r\,C^{ * }_{{\text{d}}} }}{{C^{ * }_{{\text{r}}} }}C^{{\text{2}}}_{{{\text{r1}}}} - k_{2} {\left( {\delta + \alpha C^{ * }_{{\text{r}}} } \right)}C^{2}_{1} - k_{3} {\left( {k + \nu C^{ * }_{{\text{r}}} } \right)}C^{{\text{2}}}_{{{\text{a1}}}} } \hfill} \\ {{} \hfill} & {{ - k4{\left( {\delta _{{\text{p}}} + \delta _{{{\text{p1}}}} C^{ * }_{{\text{r}}} } \right)}C^{{\text{2}}}_{{{\text{p1}}}} + k_{1} rC_{{{\text{d1}}}} C_{{{\text{r1}}}} - k_{0} \lambda _{1} C^{ * }_{{\text{d}}} C_{{{\text{d1}}}} C_{1} - k_{1} r_{1} C^{ * }_{{\text{r}}} C_{{{\text{r1}}}} C_{1} } \hfill} \\ {{} \hfill} & {{ - k_{2} {\left( {\alpha C^{ * } - \pi \nu C^{ * }_{{\text{a}}} } \right)}C_{{{\text{r1}}}} C_{1} + k_{3} {\left( {\alpha C^{ * } - \nu C^{ * }_{{\text{a}}} } \right)}C_{{{\text{r1}}}} C_{{{\text{a1}}}} - k_{1} r_{2} C^{ * }_{{\text{r}}} C_{{{\text{r1}}}} C_{{{\text{p}}1}} } \hfill} \\ {{} \hfill} & {{ - k_{4} \delta _{{{\text{p1}}}} C^{ * }_{{\text{p}}} C_{{{\text{r1}}}} C_{{{\text{p1}}}} + k2{\left( {\theta k + \pi \nu C^{ * }_{{\text{r}}} } \right)}C_{1} C_{{{\text{a1}}}} + k_{3} \alpha C^{ * }_{{\text{r}}} C_{1} C_{{{\text{a1}}}} } \hfill} \\ \end{array} $$

(A2)

For $\frac{{dV}} {{dt}}$ to be negative definite, the following inequalities must be satisfied in (A2),

$$ k_{1} r^{2} < \frac{1} {3}k_{0} \frac{{rC^{ * }_{{\text{d}}} }} {{C^{ * }_{{\text{r}}} }}{\left( {\lambda _{0} + \lambda _{1} C^{ * } } \right)} $$

$$ k_{0} {\left( {\lambda _{1} C^{ * }_{{\text{d}}} } \right)}^{2} < \frac{2} {5}k_{2} {\left( {\lambda _{0} + \lambda _{1} C^{ * } } \right)}{\left( {\delta + \alpha C^{ * }_{{\text{r}}} } \right)} $$

$$ k_{1} {\left( {r_{1} C^{ * }_{{\text{r}}} } \right)}^{2} < \frac{2} {{15}}k_{2} \frac{{rC^{ * }_{{\text{d}}} }} {{C^{ * }_{{\text{r}}} }}{\left( {\delta + \alpha C^{ * }_{{\text{r}}} } \right)} $$

$$ k_{2} {\left( {\alpha C^{ * } - \pi \nu C_{{\text{a}}}^{*} } \right)}^{2} < \frac{2} {{15}}k_{1} \frac{{rC^{ * }_{{\text{d}}} }} {{C^{ * }_{{\text{r}}} }}{\left( {\delta + \alpha C^{ * }_{{\text{r}}} } \right)} $$

$$k_{3} {\left( {\alpha C^{ * } - \nu C^{ * }_{{\text{a}}} } \right)}^{2} < \frac{2}{9}k_{1} \frac{{rC^{ * }_{{\text{d}}} }}{{C^{ * }_{{\text{r}}} }}{\left( {k + \nu C^{ * }_{{\text{r}}} } \right)}$$

$$ k_{1} {\left( {r_{2} C^{ * }_{{\text{r}}} } \right)}^{2} < \frac{1} {3}k_{4} \frac{{rC^{ * }_{{\text{d}}} }} {{C^{ * }_{{\text{r}}} }}{\left( {\delta _{{\text{p}}} + \delta _{{{\text{p1}}}} C^{ * }_{{\text{r}}} } \right)} $$

$$ k_{4} {\left( {\delta _{{{\text{p1}}}} C^{ * }_{{\text{p}}} } \right)}^{2} < \frac{1} {3}k_{1} \frac{{rC^{ * }_{{\text{d}}} }} {{C^{ * }_{{\text{r}}} }}{\left( {\delta _{{\text{p}}} + \delta _{{{\text{p1}}}} C^{ * }_{{\text{r}}} } \right)} $$

$$ k_{2} {\left( {\theta k + \pi \nu C^{ * }_{{\text{r}}} } \right)}^{2} < \frac{4} {{15}}k_{3} {\left( {\delta + \alpha C^{ * }_{{\text{r}}} } \right)}{\left( {k + \nu C^{ * }_{{\text{r}}} } \right)} $$

$$ k_{3} {\left( {\alpha C_{{\text{r}}}^{*} } \right)}^{2} < \frac{4} {{15}}k_{2} {\left( {\delta + \alpha C^{ * }_{{\text{r}}} } \right)}{\left( {k + \nu C^{ * }_{{\text{r}}} } \right)} $$

Now choosing the constants k ₁ = 1, $k_{0} > \frac{{3rC^{ * }_{{\text{r}}} }} {{C^{ * }_{{\text{d}}} {\left( {\lambda _{0} + \lambda _{1} C^{ * } } \right)}}}$, the above inequalities reduce to the following forms after some simplifications,

$$\frac{{15C^{*}_{r} }}{{2{\left( {\delta + \alpha C^{{\text{*}}}_{{\text{r}}} } \right)}}}\max {\left\{ {\frac{{r\lambda ^{2}_{1} C^{{\text{*}}}_{{\text{d}}} }}{{{\left( {\lambda _{0} + \lambda _{1} C^{*} } \right)}^{2} }},\frac{{{\left( {r_{1} C^{{\text{*}}}_{{\text{r}}} } \right)}^{2} }}{{rC^{{\text{*}}}_{{\text{d}}} }}} \right\}} < k_{2} < \frac{2}{{15}}\frac{{r{\left( {\delta + \alpha C^{{\text{*}}}_{{\text{r}}} } \right)}}}{{C^{{\text{*}}}_{{\text{r}}} {\left( {\alpha C^{*} - \pi \nu C^{{\text{*}}}_{{\text{a}}} } \right)}^{2} }}$$

(A3)

$$ 3r_{2} \delta _{{{\text{p1}}}} C^{ * }_{{\text{r}}} C^{ * }_{{\text{p}}} < \delta _{{\text{p}}} r_{0} $$

(A4)

$$ {\left( {\theta k + \pi \nu C^{ * }_{{\text{r}}} } \right)}^{2} k_{2} < \frac{8}{{15}}{\left( {\delta + \alpha C^{ * }_{{\text{r}}} } \right)}{\left( {k + C^{ * }_{{\text{r}}} } \right)}^{2} \min {\left\{ {\frac{2}{{15}}\frac{{{\left( {\delta + \alpha C^{ * }_{{\text{r}}} } \right)}}}{{{\left( {\alpha C^{ * }_{{\text{r}}} } \right)}^{2} }}k_{2} ,\frac{1}{9}\frac{{rC^{ * }_{{\text{d}}} }}{{{\left( {\alpha C^{ * } - \nu C^{ * }_{{\text{a}}} } \right)}^{2} }}} \right\}}$$

(A5)

where the coefficient k ₂ is so chosen that the inequalities (A3) and (A5) are satisfied.

Under these conditions, $\frac{{dV}} {{dt}}$ would be negative definite showing that V is Lyapunov’s function and hence the theorem.

Appendix B

Proof of the Theorem 2

To establish nonlinear asymptotic stability of E* we take the following positive definite function about E*,

$$U = \frac{1}{2}{\left[ {m_{0} {\left( {C_{{\text{d}}} - C^{*}_{{\text{d}}} } \right)}^{2} + m_{1} {\left( {C_{{\text{r}}} - C^{*}_{{\text{r}}} } \right)}^{2} + m_{2} {\left( {C - C^{*} } \right)}^{2} + m_{3} {\left( {C_{{\text{a}}} - C^{*}_{{\text{a}}} } \right)} + m_{4} {\left( {C_{{\text{p}}} - C^{*}_{{\text{p}}} } \right)}^{2} } \right]}$$

(B1)

On differentiation of (B1) and using Equations (1)–(5), we get

$$ \begin{array}{*{20}c} {\frac{{dU}} {{dt}} = {\left( {C_{{\text{d}}} - C^{ * }_{{\text{d}}} } \right)}{\left( {\lambda - \lambda _{0} C_{{\text{d}}} - \lambda _{1} C_{{\text{d}}} C} \right)} + m_{1} {\left( {C_{{\text{r}}} - C^{ * }_{{\text{r}}} } \right)}{\left( {rC_{{\text{d}}} - r_{0} C_{{\text{r}}} - r_{1} CC_{{\text{r}}} - r_{2} C_{{\text{p}}} C_{{\text{r}}} } \right)}} \\ { + m_{2} {\left( {C - C^{ * } } \right)}{\left( {Q - \delta C - \alpha CC_{{\text{r}}} + \theta kC_{{\text{a}}} + \pi \nu C_{{\text{r}}} C_{{\text{a}}} } \right)}} \\ { + m_{3} {\left( {C_{{\text{a}}} - C^{ * }_{{\text{a}}} } \right)}{\left( {\alpha CC_{{\text{r}}} - kC_{{\text{a}}} - \nu C_{{\text{r}}} C_{{\text{a}}} } \right)} + m_{4} {\left( {C_{{\text{p}}} - C^{ * }_{{\text{p}}} } \right)}{\left( {Q_{{\text{p}}} - \delta _{{\text{p}}} C_{{\text{p}}} - \delta _{{{\text{p1}}}} C_{{\text{p}}} C_{{\text{r}}} } \right)}} \\ \end{array} $$

(B2)

After some algebraic manipulations, the above equation can be written as

$$\begin{array}{*{20}l} {\frac{{dU}}{{dt}} = - m{\left( {r_{1} C + r_{2} C_{{\text{p}}} } \right)}{\left( {C_{{\text{r}}} - C^{ * }_{{\text{r}}} } \right)}^{2} - m_{2} \alpha C_{{\text{r}}} {\left( {C - C^{ * } } \right)}^{2} - m_{4} \delta _{{{\text{p1}}}} C_{{\text{r}}} {\left( {C_{{\text{p}}} - C^{ * }_{{\text{p}}} } \right)}^{2} } \\{{} - m_{0} {\left( {\lambda _{0} + \lambda _{1} C^{ * } } \right)}{\left( {C_{{\text{d}}} - C^{ * }_{{\text{d}}} } \right)}^{2} - m_{1} r_{0} {\left( {C_{r} - C^{ * }_{{\text{r}}} } \right)}^{2} - m_{2} \delta {\left( {C - C^{ * } } \right)}^{2} - m_{3} {\left( {k + \nu C^{ * }_{{\text{r}}} } \right)}{\left( {C_{{\text{a}}} - C^{ * }_{{\text{a}}} } \right)}^{2} } \\{{} - m_{4} \delta _{{\text{p}}} {\left( {C_{{\text{p}}} - C^{ * }_{{\text{p}}} } \right)}^{2} - m_{0} \lambda _{1} C^{ * }_{{\text{d}}} {\left( {C_{{\text{d}}} - C^{ * }_{{\text{d}}} } \right)}{\left( {C - C^{ * } } \right)} + m_{1} r{\left( {C_{{\text{d}}} - C^{ * }_{{\text{d}}} } \right)}{\left( {C_{{\text{r}}} - C^{ * }_{{\text{r}}} } \right)}} \\{{} - m_{1} r_{1} C^{ * }_{{\text{r}}} {\left( {C_{{\text{r}}} - C^{ * }_{{\text{r}}} } \right)}{\left( {C - C^{ * } } \right)} - m_{2} {\left( {\alpha C^{ * } - \pi \nu C^{ * }_{{\text{a}}} } \right)}{\left( {C_{{\text{r}}} - C^{ * }_{{\text{r}}} } \right)}{\left( {C - C^{ * } } \right)}} \\{{} - m_{1} r_{2} C^{ * }_{r} {\left( {C_{{\text{r}}} - C^{ * }_{{\text{r}}} } \right)}{\left( {C_{{\text{p}}} - C^{ * }_{{\text{p}}} } \right)} - m_{4} \delta _{{{\text{p1}}}} C^{ * }_{{\text{p}}} {\left( {C_{{\text{r}}} - C^{ * }_{{\text{r}}} } \right)}{\left( {C_{{\text{p}}} - C^{ * }_{{\text{p}}} } \right)}} \\{{} + m_{3} {\left( {\alpha C^{ * } - \nu C^{ * }_{{\text{a}}} } \right)}{\left( {C_{r} - C^{ * }_{r} } \right)}{\left( {C_{{\text{a}}} - C^{ * }_{{\text{a}}} } \right)} + m_{2} {\left( {\theta k + \pi \nu C_{{\text{r}}} } \right)}{\left( {C - C^{ * } } \right)}{\left( {C_{{\text{a}}} - C^{ * }_{{\text{a}}} } \right)}} \\{{} + m_{3} \alpha C_{{\text{r}}} {\left( {C - C^{ * } } \right)}{\left( {C_{{\text{a}}} - C^{ * }_{{\text{a}}} } \right)}} \\ \end{array} $$

(B3)

Now $\frac{{dU}} {{dt}}$ will be negative definite if the following inequalities are satisfied:

$$ m_{1} r^{2} < \frac{1} {3}m_{0} r_{0} \lambda _{0} $$

$$ m_{0} {\left( {\lambda _{1} C^{ * }_{{\text{d}}} } \right)}^{2} < \frac{2} {5}m_{2} \lambda _{0} \delta $$

$$ m_{1} {\left( {r_{1} C^{ * }_{{\text{r}}} } \right)}^{2} < \frac{2} {{15}}m_{2} r_{0} \delta $$

$$m_{2} {\left( {dC^{ * } - \pi \nu C^{ * }_{{\text{a}}} } \right)}^{2} < \frac{2}{{15}}m_{1} r_{0} \delta $$

$$ m_{3} {\left( {\alpha C^{ * } + \nu C_{{\text{a}}} } \right)}^{2} < \frac{2} {9}m_{1} r_{0} {\left( {k + \nu C^{ * }_{{\text{r}}} } \right)} $$

$$ m_{4} {\left( {\delta _{{{\text{p1}}}} C_{{\text{p}}} } \right)}^{2} < \frac{1} {3}m_{1} r_{0} \delta _{{\text{p}}} $$

$$m_{{\text{1}}} {\left( {r_{2} C^{*}_{r} } \right)}^{2} < \frac{1}{3}m_{4} r_{0} \delta _{p} $$

$$ m_{2} {\left( {\theta k + \pi \nu C_{{\text{r}}} } \right)}^{2} < \frac{4} {{15}}m_{3} \delta {\left( {k + \nu C^{ * }_{{\text{r}}} } \right)} $$

$$ m_{3} {\left( {\alpha C_{{\text{r}}} } \right)}^{2} < \frac{4} {{15}}m_{2} \delta {\left( {k + \nu C^{ * }_{{\text{r}}} } \right)} $$

Now choosing appropriate values of the variables from Ω and the constants m ₁ = 1, $m_{0} > \frac{{3r}} {{r_{0} \lambda _{0} }}$ the above inequalities reduce to the following forms after some simplifications,

$$ \frac{{15}} {{2r_{0} \delta }}\max {\left\{ {\frac{{r{\left( {\lambda_{1} C^{ * }_{{\text{d}}} } \right)}^{2} }} {{\lambda ^{2}_{0} }},{\left( {r_{1} C^{ * }_{{\text{r}}} } \right)}^{2} } \right\}} < m_{2} < \frac{2} {{15}}\frac{{\delta r_{0} }} {{{\left( {\alpha C^{ * } - \pi \nu C^{ * }_{{\text{a}}} } \right)}^{2} }} $$

(B4)

$$ 3r_{2} \delta _{{{\text{p1}}}} C^{ * }_{{\text{r}}} C^{ * }_{{\text{p}}} < \delta _{{\text{p}}} r_{0} $$

(B5)

$$ {\left( {\theta k + \pi \nu \frac{{r\lambda }} {{r_{0} \lambda _{0} }}} \right)}^{2} m_{2} < \frac{8} {{15}}\delta {\left( {k + \nu C^{ * }_{{\text{r}}} } \right)}^{2} \min {\left\{ {\frac{2} {{15}}\frac{\delta } {{{\left( {\frac{{\alpha r\lambda }} {{r_{0} \lambda _{0} }}} \right)}^{2} }}m_{2} ,\frac{1} {9}\frac{{r_{0} }} {{{\left( {\alpha C^{ * } + \nu \frac{Q} {{\delta _{{\text{m}}} }}} \right)}^{2} }}} \right\}} $$

(B6)

where the coefficient m ₂ is so chosen that the inequalities (B4) and (B6) are satisfied.

Under these conditions, $\frac{{dU}} {{dt}}$ would be negative definite showing that U is Lyapunov’s function and hence the theorem.