Multivariate probabilistic projections using imperfect climate models part I: outline of methodology

Abstract

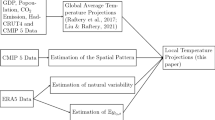
We demonstrate a method for making probabilistic projections of climate change at global and regional scales, using examples consisting of the equilibrium response to doubled CO₂ concentrations of global annual mean temperature and regional climate changes in summer and winter temperature and precipitation over Northern Europe and England-Wales. This method combines information from a perturbed physics ensemble, a set of international climate models, and observations. Our approach is based on a multivariate Bayesian framework which enables the prediction of a joint probability distribution for several variables constrained by more than one observational metric. This is important if different sets of impacts scientists are to use these probabilistic projections to make coherent forecasts for the impacts of climate change, by inputting several uncertain climate variables into their impacts models. Unlike a single metric, multiple metrics reduce the risk of rewarding a model variant which scores well due to a fortuitous compensation of errors rather than because it is providing a realistic simulation of the observed quantity. We provide some physical interpretation of how the key metrics constrain our probabilistic projections. The method also has a quantity, called discrepancy, which represents the degree of imperfection in the climate model i.e. it measures the extent to which missing processes, choices of parameterisation schemes and approximations in the climate model affect our ability to use outputs from climate models to make inferences about the real system. Other studies have, sometimes without realising it, treated the climate model as if it had no model error. We show that omission of discrepancy increases the risk of making over-confident predictions. Discrepancy also provides a transparent way of incorporating improvements in subsequent generations of climate models into probabilistic assessments. The set of international climate models is used to derive some numbers for the discrepancy term for the perturbed physics ensemble, and associated caveats with doing this are discussed.

Appendices

Appendix 1: Making eigenvectors of multiple variables

First, we decide which model variables e.g. cloud amount, 1.5 m temperature to include. We use N _var  = 48 variables (4 seasons  ×  12 variables described in Table 1 of Sect. 2). Then, we construct an N _e  × N _o data matrix $D^{\prime}$, where N _e is the number of members in the PPE i.e. 280 here, and N _o is the number of observable quantities over all locations and variable types. For each ensemble member, we concatenate all the grid-point/zonally-averaged data where observations exist for all the model variables under consideration into one long vector, length N _o . Then we centre each observed quantity by removing its ensemble mean d _i where $i=1,\ldots,N_o$. Before we reduce dimensionality we must non-dimensionalise the data in D. In a similar way to Piani et al. (2005), we do this for each model variable by first calculating a global measure of scale, which is the root mean square of the standard deviation at each grid point in a set trimmed by only using those between the 1st and 99th percentile; the trimming stops grid-points of high variance across the ensemble e.g. near sea-ice margins, dominating the eigenvector analysis. Then for each variable, we rescale its values in each grid-box by that variable’s global scaling factor, ξ _j where $j=1, \ldots, N_{var}$. Therefore for each climate variable, we non-dimensionalise the data whilst retaining the relative geographical variations in variance. Finally each observable is area-weighted by the square root of the grid-box/zonal area, w _i ; multi-level fields are divided by the number of pressure levels so that one multi-level field has the same overall weight as a single level horizontal field. The columns for each member, D _(k) where $k=1,\ldots,N_e$ are combined to form a matrix D which has a column of length N _o and a row of length N _e . That is,

$$ D = (D^{\prime} - 1 d^T) \xi^{-1} W^{-1}, $$

(14)

where d is a vector, length N _o of the ensemble mean d _i , ξ is a diagonal matrix containing the appropriate global scaling factor for each element of d, and W is a diagonal matrix of the square root of the area weights, a _i .

SVD calculates the left vectors, U, eigenvalues, $\Uplambda$ and right vectors, V so that

$$ D = U \Uplambda V^T. $$

(15)

This implies that the covariance of the ensemble data, $\frac{1}{N_e-1}D^T D$, has eigenvectors V and eigenvalues $\frac{1}{N_e-1} \Uplambda_i^2$. Also, the matrix $A = U \Uplambda = DV$ is now the set of amplitudes, A _ki of how the kth ensemble member D _(k) projects onto the ith eigenvector V _(i).

Similarly, we non-dimensionalise the observations and project them onto the set of eigenvectors, so that we have the N _e -length vector of amplitudes for each eigenvector, $o^T=(o^{{\prime} T}-d^T) \xi^{-1} W^{-1} V$ where $o^{\prime}$ are the corresponding observed values for the data used to make $D^{\prime}$. The same procedure has to be applied to the multimodel data used to specify the discrepancy.

To display the eigenvectors in Figs. 2 and 3 we show patterns of variation about the mean if the amplitude was set to one standard deviation of the amplitudes for the ith eigenvector, which is $\left[\frac{1}{N_e-1} \Uplambda_i^2\right]^{\frac{1}{2}}$. The area-weighting and normalising has to be reversed so in Figs. 2 and 3 we show subsets of the vector $\left[\frac{1}{N_e-1}\right]^{\frac{1}{2}}\Uplambda_i V_{(i)} W \xi$.

Appendix 2: Emulators

2.1 2.1 Building a univariate emulator

An emulator is used to predict model output for any combination of parameter values based on the ensemble of model evaluations. In this section, we discuss the method to emulate historical climate and the equilibrium response to doubled CO₂ and so we use the ensemble of HadSM3 simulations that sample atmospheric parameter space, χ, which had ensemble size, N _e  = 280. We chose a relatively simple method for automatically constructing these emulators using standard regression tools and a simple diagnostic which measures the normality of the residuals.

We build an emulator for each model variable, Y, using classical linear regression to relate Y to functions of the atmospheric parameter values. A stepwise algorithm was used to remove redundant regressors. The general regression model for our emulator is

$$ {\fancyscript{B}}(Y ; s, \theta_1, \theta_2) = \sum_{k=1}^p \gamma_k g_k(l(X)) + \eta. $$

(16)

where p is the number of regressors and η is the regression error. To help satisfy the requirement that our emulators are Gaussian, we use the Box–Cox transformation of a variable y (Draper and Smith 1998)

$$ {\fancyscript{B}}(Y ; s, \theta_1, \theta_2) = \left\{ { \begin{array}{l} { log(s Y-\theta_2), \quad \theta_1=0} \\ { (s Y-\theta_2)^{\theta_1}, \quad \theta_1 \not= 0,} \end{array} } \right. $$

(17)

parameterised by s which can be ±1, θ₁, and θ₂ where sY − θ₂ > 0.

We define the full set of regressors to consider. In our study, these are functions $g_i(\cdot)$ of l(X) where l(X) = X for all parameters, or l(X) is a mixture of X for discrete parameters and log(X) for continuous ones (see below for how l(X) is selected). Here, we allow $g_i(\cdot)$ to be quadratics in the continuous parameters and two-way interactions between the continuous parameters. We use three-way interactions between RH _crit (the threshold of relative humidity for cloud formation), V _f1 (ice fallout speed), C _wland (cloud droplet to rain conversion threshold), and C _t (cloud droplet to rain conversion rate), ENT (entrainment rate coefficient), and EACFBL (cloud fraction at gridbox saturation), as these have been found by Rougier et al. (2009) to be important in emulating the climate sensitivity across the climateprediction.net ensemble (Stainforth et al. 2005).

The stepwise algorithm used here does not allow lower order terms for variables to be dropped if higher order terms are present which include those variables; this makes the statistical model robust to changes of scale (Draper and Smith 1998). We also ensure that not too many regressors are retained by preventing the residual variance going below the level of internal variability (see Sect. 2.4). The stepwise method is used on all four combinations of s =  ±1 and l(X) that are considered. As there is an emulator for each historic and future climate variable that we need to predict, and there are a large number of these, an automatic method is required to decide which combination of transformations ${\fancyscript{B}(Y)}$ and l(X) is best. We use a diagnostic which measures the degree of normality of the residuals as the p value from the Kolmogorov–Smirnov test that the residuals are Gaussian. For those statistical models with a p value >0.2, we chose the one with the lowest residual sum of squares in the units of Y. If all statistical models fail the test that the residuals are Gaussian, we pick the best one in terms of residual sum of squares but flag the emulator as a potentially bad one.

It is important to not make the number of functions, $g_i(\cdot)$ too large as this can lead to over-fitting. Rougier et al. (2009) show diagnostics that can be used to check the emulator. We used their leave-one-out cross-validation test where each ensemble member is omitted and the other runs are used to re-estimate the regression parameters in the emulator and then predict the omitted run. Supplementary Information Figs. 1 and 2 show the results for historical and future variables respectively, and show that across all variables between 12 and 20 actual values fall outside the 95% credible intervals predicted by the emulator. We would expect by chance, from an ensemble of size 280, to have between 8 and 20 values fall outside so the emulators seem satisfactory. We also used quantile-quantile plots to test that the residuals are consistent with the Gaussian assumption (see Supplementary Information Figs. 3 and 4). The leave-one-out tests are not independent as the predictions are correlated across the ensemble, so Rougier et al. (2009) outline a sterner multivariate test where a randomly selected third of the ensemble are left out and the emulator is constructed from the remaining 187 members. Supplementary Information Figs. 5 and 6 shows the results from the leave-93-out cross-validation tests. The emulators passed both these tests. Finally, we checked that the emulator for the future climate variables does not predict a large fraction of the Monte Carlo sample lie outside the range of values sampled by the ensemble.

2.2 2.2 Estimating covariance matrix for multivariate emulator

In Eq. 10 we have to estimate the covariance matrix $\Upsigma^{em}(x)$ that depends on the point in parameter space, x. There is no established way of estimating the covariance matrix for a multivariate emulator where each emulator differs in its set of regressors. We apply standard mathematical techniques to estimate the covariance between the emulators of the ith and jth climate variables at parameter point x, Cov(μ _i (x),μ _j (x)) where μ _i (x) = ∑ ^p _k=1 γ _ik g _ik (l(x)) or in matrix notation, μ _i (x) = G _i γ _i where G _i is a matrix where each row is g _i (l(X)) and X are the parameter sampled values for the model parameters. First we need to know the covariance matrix of the errors, Var(η). The covariance between residuals in the ith emulator, η _i , and the jth emulator, η _j , can be estimated as

$$ \frac{1}{[(N_e-q_i)(N_e-q_j)]^{\frac{1}{2}}} \eta_i \cdot \eta_j $$

(18)

where q _i is the number of regression parameters in the ith emulator.

For the ith emulator with regressors G _i we have

$$ G_i\hat{\gamma_i} - G_i\gamma_i = G_i(G_i^{T} G_i)^{-1} G_i^{T} Y - G_i\gamma_i \\ $$

(19)

$$ = G_i(G_i^{T} G_i)^{-1} G_i^{T} (\eta_i + G_i\gamma_i)- G_i\gamma_i \\ $$

(20)

$$ = G_i(G_i^{T} G_i)^{-1} G_i^{T} \eta_i\\ $$

(21)

so that, since G _i has full common rank,

$$ \hat{\gamma_i} - \gamma_i = (G_i^{T} G_i)^{-1} G_i^{T} \eta_i \\ $$

(22)

$$ = H_i \eta_i. \\ $$

(23)

Then we have

$$ Cov(\gamma_i \gamma_j) = {\rm Var}(\eta)_{ij} H_i H_j^{T} $$

(24)

and it follows that

$$ \hbox{Cov}(\mu_i(x), \mu_j(x)) = \hbox{Var}(\eta)_{ij} \left(1 + [H_i^{T} g_i(x)]^{T} [H_j^{T} g_j(x)] \right). $$

(25)

where the first component comes from the error variance and the second component comes from the regressors of the two emulators.