Abstract
One defining property of granular materials is their low number of constituents when compared to molecular systems. This implies that (statistical) fluctuations can have a dominant effect on the global dynamics of the system. In the following we create identical time-averaged macroscopic states with significantly different numbers of particles in order to directly study the role of fluctuations in granular systems. The dependency of the hydrodynamic conservation equations on the particles' size is derived, which directly relates to different particle–number densities. We show that, provided that the particles' dissipation is properly scaled, equivalent states can be obtained in the small particle size limit. Simulations of the granular Leidenfrost state confirm the validity of the scalings, and allow us to study the effects of fluctuations on collective oscillations. We observe that the amplitude of these oscillations decreases with the square root of the number of particles, while their frequency remains constant.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Granular flows often show a remarkable similarity with those of molecular fluids [1, 2]. The success of granular hydrodynamic theories in predicting many complex granular behaviours indicates that such a relation is not only superficial [3–9]. But despite continued development, the defining properties of granular materials, such as the dissipative nature of the particles' interactions, still present a challenge for continuum theories, specially for high packing densities or strong dissipations [10–12]. An additional fundamental difficulty stems from the enormous difference in the total number of constituents between granular and molecular systems; while in molecular media the microscopic relevant length-scale is orders of magnitude smaller than the macroscopic one, in granular media macroscopic fields may vary in distances of the order of a few particle diameters. This possibly big influence of a few particles on macroscopic quantities implies the existence of inherently large fluctuations, which can drastically modify the global dynamics, especially near transitions [13–15]. Deepening our understanding of the role played by these fluctuations is thus of fundamental importance for the development of a successful continuum description of granular media.
In the following paper we first analyse the influence that finite-number-driven fluctuations have on the macroscopic states of flowing granular matter. For this, we study the possibility of constructing macroscopically identical granular systems with significantly different number of particles. Starting from a given macroscopic hydrodynamic state, and using physical arguments and expressions for the transport coefficients from granular hydrodynamic models, we derive the dependency on particle size of all terms of the conservation laws. As in systems with the same macroscopic density the particle size is directly related to the total number of particles, we essentially see the dependency of the macroscopic states on the total number of particles present in the system. We demonstrate that in general the granular hydrodynamic equations are not particle-size invariant. Nevertheless, we show that, by properly scaling the restitution coefficient, the limit of vanishing particle size becomes well defined and leads to invariant conservation equations. Although superficially our scaling analysis is similar to earlier studies of the granular hydrodynamic equations, our purpose is a very different one, namely the investigation of whether it is possible to construct a hydrodynamic formulation that, given the macroscopic fields, remains invariant when changing the size of the particles, and therewith with the total particle number.
Subsequently, to study the relevance of the total number of particles on the strength of fluctuations in flowing granular matter we focus on the granular Leidenfrost state [7, 16, 17]. Using hard-sphere simulations and the derived scalings we create systems with up to four orders of magnitude difference in the particle number density with identical average hydrodynamic fields. Although in average the systems are identical, the amplitude of the oscillations previously observed in the granular Leidenfrost state are seen to decrease with the number of particles while, surprisingly, the frequency of these oscillations remains invariant.
2. Granular hydrodynamic scaling relations
In the following we study the particle-size dependency of the three-dimensional granular hydrodynamic equations. Our goal is to recreate equivalent hydrodynamic states with significantly different total numbers of particles N. Two hydrodynamic states are considered identical if the time-averaged invariant macroscopic hydrodynamic fields are the same in all space. As invariant hydrodynamic fields, functions of the spatial coordinates  and time t, we consider the packing fraction,
and time t, we consider the packing fraction,  , the velocity
, the velocity 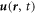 , and the fluctuations in velocity
, and the fluctuations in velocity  . All these are obtained from the position and velocities of the particles,
. All these are obtained from the position and velocities of the particles,  and
and  , through a coarse-graining procedure. The packing fraction is given by
, through a coarse-graining procedure. The packing fraction is given by  , with m, d and
, with m, d and  the mass, diameter and density of the particles. The number density field is a convolution of the particles' positions,
the mass, diameter and density of the particles. The number density field is a convolution of the particles' positions,  , where
, where  is a smoothing or coarse-graining function, i.e., a continuous and integrable replacement of the Dirac delta function which allows us to obtain well defined macroscopic quantities [18, 19]. The velocity field is then
is a smoothing or coarse-graining function, i.e., a continuous and integrable replacement of the Dirac delta function which allows us to obtain well defined macroscopic quantities [18, 19]. The velocity field is then 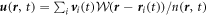 . Finally the fluctuations in velocity
. Finally the fluctuations in velocity  , with
, with  the granular temperature field, and kB the granular equivalent of the Boltzmann constant5
. Strong invariance would imply the same packing fraction, velocity and granular temperature distributions in space and time for systems with different number of particles and initial conditions. Naturally, this condition is too strong for what are essentially fluctuating systems, and we therefore focus on invariance of the fields averaged over a timescale τ larger than fluctuations driven by the microscopic scale, in which case we say that the systems are equivalent.
the granular temperature field, and kB the granular equivalent of the Boltzmann constant5
. Strong invariance would imply the same packing fraction, velocity and granular temperature distributions in space and time for systems with different number of particles and initial conditions. Naturally, this condition is too strong for what are essentially fluctuating systems, and we therefore focus on invariance of the fields averaged over a timescale τ larger than fluctuations driven by the microscopic scale, in which case we say that the systems are equivalent.
In terms of these macroscopic fields the granular hydrodynamic equations can be written as:
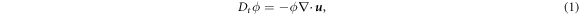

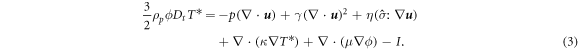
where  is the material derivative,
is the material derivative,  the identity matrix and the deviatoric strain rate
the identity matrix and the deviatoric strain rate 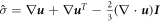 . These correspond to the mass conservation equation; the momentum conservation equation, with p the pressure,
. These correspond to the mass conservation equation; the momentum conservation equation, with p the pressure,  the shear viscosity, γ the second viscosity and
the shear viscosity, γ the second viscosity and  the acceleration of gravity; and the granular temperature equation, i.e. energy balance, with κ the coefficient of thermal conductivity (note that Fourier's heat law has been used),
the acceleration of gravity; and the granular temperature equation, i.e. energy balance, with κ the coefficient of thermal conductivity (note that Fourier's heat law has been used),  an additional transport coefficient present in granular media, and
an additional transport coefficient present in granular media, and  the sink of energy-density.
the sink of energy-density.
In order for equations (1)–(3) to be d-invariant all terms of any equation should scale equally with d. In what follows we determine these scaling relations, starting with heuristic arguments and, after that, using a specific closure for the transport coefficients and the sink term available in the literature.
First, note that the continuity equation is manifestly invariant, since it only contains hydrodynamic fields and its derivatives, which are by definition identical in equivalent systems. Similarly, the left-hand terms of (2) and (3), as well as the gravitational term in (2), are also d-invariant, if we assume that the particles are made of the same material, i.e., that their density  is independent of their size. In principle, one could let
is independent of their size. In principle, one could let 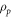 scale in any arbitrary way with the particle size, but this would lead to the same conclusions, only complicating the algebra. Additionally, the pressure is proportional to the ideal gas law (
scale in any arbitrary way with the particle size, but this would lead to the same conclusions, only complicating the algebra. Additionally, the pressure is proportional to the ideal gas law ( ) multiplied by a function of the packing fraction only, and therefore the terms in (2) and (3) involving the pressure are also d-invariant.
) multiplied by a function of the packing fraction only, and therefore the terms in (2) and (3) involving the pressure are also d-invariant.
The dependency of the transport coefficients on the size of the particles can be deduced from physical arguments. Transport of mass, momentum or energy from one fluid element into a neighbouring one happens in a layer that has a thickness scaling with the mean free path,  . Since the packing fraction ϕ is invariant,
. Since the packing fraction ϕ is invariant,  should be proportional to the particle diameter d. Therefore all terms in (2) and (3) involving the transport coefficients
should be proportional to the particle diameter d. Therefore all terms in (2) and (3) involving the transport coefficients  , γ, κ and
, γ, κ and  are expected to scale as d1.
are expected to scale as d1.
In contrast, the dissipation term I can be expressed as the number density squared (scaling as  ) times the energy loss per collision (∼d3) times the cross-sectional area (∼d2), leading to
) times the energy loss per collision (∼d3) times the cross-sectional area (∼d2), leading to  . Physically this stands to reason: when the particle size decreases, the growth of the number of collisions is faster than the shrinking of the typical energy loss per collision, and therefore the dissipation per unit volume increases.
. Physically this stands to reason: when the particle size decreases, the growth of the number of collisions is faster than the shrinking of the typical energy loss per collision, and therefore the dissipation per unit volume increases.
Using square brackets, ![${\left[x\right]}_{d}$](https://content.cld.iop.org/journals/2399-6528/3/3/035006/revision2/jpcoab034aieqn30.gif) , to denote the scaling of a quantity x with d, the above discussion is summarized as
, to denote the scaling of a quantity x with d, the above discussion is summarized as
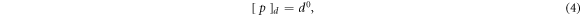
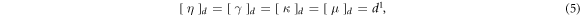

The immediate conclusion is that the general granular hydrodynamic model (1)–(3) is not d-invariant, since it contain terms that scale differently with particle size. In fact, when the particle size decreases, all transport terms decrease, whereas the energy sink term increases. In general, it is therefore not possible to create identical hydrodynamic states with (significantly) different numbers of particles.
Even if we consider a steady state ( ) without macroscopic flow (
) without macroscopic flow ( ), in which case equations (1)–(3) reduce to
), in which case equations (1)–(3) reduce to
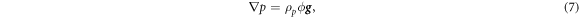
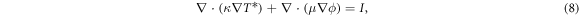
the conservation of momentum (7) is d-invariant, while conservation of energy (8) still isn't. However, for small d (with respect to the typical scale of variations of the fields, L) invariance can be obtained to order  . Both I and
. Both I and  are proportional to the inelasticity
are proportional to the inelasticity 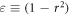 , where r is the coefficient of normal restitution. If we now let r depend on the particle diameter d such that
, where r is the coefficient of normal restitution. If we now let r depend on the particle diameter d such that
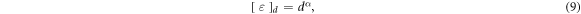
for α > 1 the 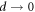 limit becomes well defined. In what follows we choose α = 2, not only for being the next natural number that leads to convergence, but also to make the dissipation I scale as the heat-flux κ, which will become useful when studying the equivalent vibrated systems. This also implies
limit becomes well defined. In what follows we choose α = 2, not only for being the next natural number that leads to convergence, but also to make the dissipation I scale as the heat-flux κ, which will become useful when studying the equivalent vibrated systems. This also implies ![${\left[\mu \right]}_{d}={d}^{3}$](https://content.cld.iop.org/journals/2399-6528/3/3/035006/revision2/jpcoab034aieqn37.gif) , as will be demonstrated further below. Therefore, as the number of particle increases, the influence of the granular transport coefficient diminishes rapidly (as d3) rendering the set of equations (7)–(8) independent of d to second order.
, as will be demonstrated further below. Therefore, as the number of particle increases, the influence of the granular transport coefficient diminishes rapidly (as d3) rendering the set of equations (7)–(8) independent of d to second order.
When the condition (9) is used in the general flow case then, for small d, equations (1)–(3) result in
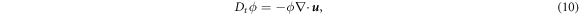
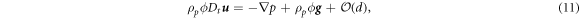

Notice that in the limit  , the above equations converge to those of a perfect (non-dissipative) fluid. Nevertheless, it is important to remark that solutions to these equations are not expected to coincide with solutions of equations (1)–(3) in the
, the above equations converge to those of a perfect (non-dissipative) fluid. Nevertheless, it is important to remark that solutions to these equations are not expected to coincide with solutions of equations (1)–(3) in the  limit (i.e. the order of the limits is crucial). For example, it is clear that the absence of dissipation in equations (10)–(12) will fail to capture the steady state of any driven granular system, as energy would continue to increase indefinitely. Convergence at d = 0 can thus be expected only for non-driven system, where the steady state corresponds to all material being motionless.
limit (i.e. the order of the limits is crucial). For example, it is clear that the absence of dissipation in equations (10)–(12) will fail to capture the steady state of any driven granular system, as energy would continue to increase indefinitely. Convergence at d = 0 can thus be expected only for non-driven system, where the steady state corresponds to all material being motionless.
3. Direct derivation of the scaling
We will now explicitly derive the dependency of the transport coefficients on d considering the expressions obtained by Garzó and Dufty, who used the Chapman-Enskog method to solve the kinetc equation of the Revised Enskog Theory [20, 21]. When expanded using Sonine polynomials, the transport coefficients χ take the general form  , where χ0 are the values for the low-density and elastic limit [21]. The corrections for excluded-volume and finite dissipation
, where χ0 are the values for the low-density and elastic limit [21]. The corrections for excluded-volume and finite dissipation  are quite involved; here we are just interested in the fact that they depend only on the packing fraction ϕ and the inelasticity ε.
are quite involved; here we are just interested in the fact that they depend only on the packing fraction ϕ and the inelasticity ε.
The low-density and elastic limit expressions of all transport coefficients can be expressed as functions of 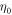 , as
, as  ,
,  and
and  [21]. Their explicit form is given by
[21]. Their explicit form is given by 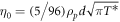 . The energy-density dissipation term follows a similar expression,
. The energy-density dissipation term follows a similar expression,
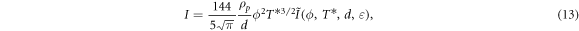
To analyse the influence of finite inelasticity, the functions  can be expanded in terms of ε, which yields
can be expanded in terms of ε, which yields

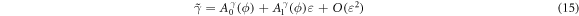
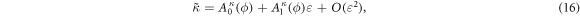

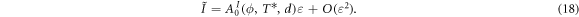
with the A coefficients depending only on the shown quantities. The dependency on d of the dissipation constant has the form 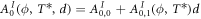 . We then see that for small dissipations, that is, to leading order in eqs.(14)–(18),
. We then see that for small dissipations, that is, to leading order in eqs.(14)–(18), ![${\left[\eta \right]}_{d}$](https://content.cld.iop.org/journals/2399-6528/3/3/035006/revision2/jpcoab034aieqn49.gif) ,
, ![${\left[\gamma \right]}_{d}$](https://content.cld.iop.org/journals/2399-6528/3/3/035006/revision2/jpcoab034aieqn50.gif) and
and ![${\left[\kappa \right]}_{d}$](https://content.cld.iop.org/journals/2399-6528/3/3/035006/revision2/jpcoab034aieqn51.gif) remain unchanged, while
remain unchanged, while ![${\left[\mu \right]}_{d}=d{\left[\varepsilon \right]}_{d}$](https://content.cld.iop.org/journals/2399-6528/3/3/035006/revision2/jpcoab034aieqn52.gif) and
and ![${\left[I\right]}_{d}={d}^{-1}{\left[\varepsilon \right]}_{d}+{\left[\varepsilon \right]}_{d}$](https://content.cld.iop.org/journals/2399-6528/3/3/035006/revision2/jpcoab034aieqn53.gif) . If then the dissipation is scaled as equation (9), I does no longer diverge when
. If then the dissipation is scaled as equation (9), I does no longer diverge when  , as
, as ![${\left[I\right]}_{d}=d+O({d}^{2})$](https://content.cld.iop.org/journals/2399-6528/3/3/035006/revision2/jpcoab034aieqn55.gif) , and
, and  decreases faster than the other transport coefficients,
decreases faster than the other transport coefficients, ![${\left[\mu \right]}_{d}={d}^{3}$](https://content.cld.iop.org/journals/2399-6528/3/3/035006/revision2/jpcoab034aieqn57.gif) . Therefore, we see that the derived scalings agree with our physical argumentation based on the mean free path, which leads to (5)–(6).
. Therefore, we see that the derived scalings agree with our physical argumentation based on the mean free path, which leads to (5)–(6).
In summary, we have derived how the transport coefficients scale explicitly on d. We have seen that a general hydrodynamic flow is not invariant on d, as is to be expected. Nevertheless, invariance can be obtained up to order d3 in steady states by assuming a particular scaling of the restitution coefficient, such that  . We now consider a specific granular system and generate equivalent average steady states, which allows us to study the driving mechanism behind an observed collective oscillating behavior.
. We now consider a specific granular system and generate equivalent average steady states, which allows us to study the driving mechanism behind an observed collective oscillating behavior.
4. Granular Leidenfrost state
We consider the granular Leidenfrost state, which consists of a density inverted particle arrangement where a high temperature, gaseous region near a vibrating bottom wall sustains a denser, colder bed of grains on top [16, 17]. As the granular Leidenfrost state corresponds to a steady state with no flow, it is expected to be described by equations (7)–(8) (with appropriate excluded volume corrections) [7, 16]. If the energy input is increased, the bed of grains goes through a transition to a buoyancy-driven convective state [15, 22]. Here we avoid this transition by considering a quasi-one-dimensional geometry with base dimensions  , with h the height of the granular column, thus preventing through geometrical constraints the development of convection [23].
, with h the height of the granular column, thus preventing through geometrical constraints the development of convection [23].
4.1. Boundary conditions
In order for the macroscopic system to be completely defined only the set of boundary conditions rests to be determined. At steady states the injected energy must be equal to the total dissipated energy. To account for the energy injection through particle-bottom wall collisions, equation (8) is integrated over the whole domain, resulting in
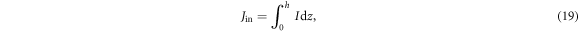
where 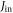 is the energy-density flux injected to the system through particle collisions with the bottom boundary. We have considered that at the free top boundary
is the energy-density flux injected to the system through particle collisions with the bottom boundary. We have considered that at the free top boundary  as
as  . In order to simplify our system we consider periodic boundary conditions in the lateral directions, and thus only the bottom wall injects energy.
. In order to simplify our system we consider periodic boundary conditions in the lateral directions, and thus only the bottom wall injects energy.  can be analytically determined in the dilute limit for a sinusoidal driving of amplitude a and angular frequency ω, when
can be analytically determined in the dilute limit for a sinusoidal driving of amplitude a and angular frequency ω, when  [24, 25], a condition expected to be valid in the Leidenfrost state, leading to
[24, 25], a condition expected to be valid in the Leidenfrost state, leading to
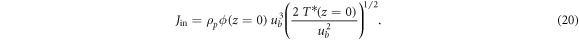
Therefore, using our previously derived scalings, and imposing that ![${\left[h\right]}_{d}={d}^{0}$](https://content.cld.iop.org/journals/2399-6528/3/3/035006/revision2/jpcoab034aieqn65.gif) , it is straightforward to see that, by (19),
, it is straightforward to see that, by (19), ![${\left[{u}_{b}^{2}\right]}_{d}={d}^{1}$](https://content.cld.iop.org/journals/2399-6528/3/3/035006/revision2/jpcoab034aieqn66.gif) , and thus
, and thus ![${\left[a\omega \right]}_{d}={d}^{1/2}$](https://content.cld.iop.org/journals/2399-6528/3/3/035006/revision2/jpcoab034aieqn67.gif) . In our case we use
. In our case we use ![${\left[a\right]}_{d}={d}^{1}$](https://content.cld.iop.org/journals/2399-6528/3/3/035006/revision2/jpcoab034aieqn68.gif) , to make sure that the amplitude remains smaller than the particle size in the limit
, to make sure that the amplitude remains smaller than the particle size in the limit  . It then follows that
. It then follows that
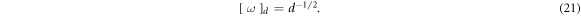
The balance of energy (19) also indicates that the relevant number of particles must be considered per unit base area, 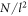 , as in equilibrium the particles in a vertical section dissipate the energy injected by the vibrations of the column's base area. As
, as in equilibrium the particles in a vertical section dissipate the energy injected by the vibrations of the column's base area. As  , with Ω the domain, from the definition and d-invariance of ϕ we see that
, with Ω the domain, from the definition and d-invariance of ϕ we see that

In order to reduce the total number of particles in the system and thus decrease the computation time, the dimensions of the container are scaled such that ![${\left[{l}^{2}\right]}_{d}={d}^{2}$](https://content.cld.iop.org/journals/2399-6528/3/3/035006/revision2/jpcoab034aieqn72.gif) .
.
4.2. Dimensionless quantities
We now derive how the relevant dimensionless numbers for the Leidenfrost system scale with d. The amount of particles is correctly quantified independent of the system's size by the number of filling layers  . From (22) it is clear that
. From (22) it is clear that ![${\left[F\right]}_{d}={d}^{-1}$](https://content.cld.iop.org/journals/2399-6528/3/3/035006/revision2/jpcoab034aieqn74.gif) . The shaking strength
. The shaking strength  is known to be a good control parameter for the transition to buoyancy-driven convection in wider systems [17]. It follows from (21) that
is known to be a good control parameter for the transition to buoyancy-driven convection in wider systems [17]. It follows from (21) that ![${\left[{S}_{f}\right]}_{d}={d}^{0}$](https://content.cld.iop.org/journals/2399-6528/3/3/035006/revision2/jpcoab034aieqn76.gif) , suggesting that the critical points of the transition could be d-invariant, a possible motivation for future research. Finally, the Reynolds number quantifies the relative importance of inertial to viscous forces,
, suggesting that the critical points of the transition could be d-invariant, a possible motivation for future research. Finally, the Reynolds number quantifies the relative importance of inertial to viscous forces,  . Using (5), we see that
. Using (5), we see that ![${\left[\mathrm{Re}\right]}_{d}={d}^{-1}$](https://content.cld.iop.org/journals/2399-6528/3/3/035006/revision2/jpcoab034aieqn78.gif) . The divergence for
. The divergence for  is expected, as we have seen that in that limit the fluid posseses no viscosity.
is expected, as we have seen that in that limit the fluid posseses no viscosity.
5. Simulations
Numerical simulations are performed using the event-driven discrete particle method [26]. For details about the algorithm's characteristics we refer the reader to [23]. As in the theoretical model, we assume collisions are determined by a single coefficient of restitution r. Different systems are referred to as  , with the variables' subscripts denoting the specific d. In order to produce equivalent systems a reference one must be defined, which we take to be
, with the variables' subscripts denoting the specific d. In order to produce equivalent systems a reference one must be defined, which we take to be  , and use d1 = 1 as length-scale for all systems. Time is measured with respect to the acceleration of gravity, in units of
, and use d1 = 1 as length-scale for all systems. Time is measured with respect to the acceleration of gravity, in units of  .
.
Following the theoretical analysis, we scale the amplitude proportional to d,  , such that
, such that  . The small prefactor is chosen to minimize the spatial inhomogeneities induced by higher oscillation amplitudes, and thus approach the limit of an effective fixed temperature boundary condition [27]. The frequency of oscillation is taken such that the system is well within the Leidenfrost state,
. The small prefactor is chosen to minimize the spatial inhomogeneities induced by higher oscillation amplitudes, and thus approach the limit of an effective fixed temperature boundary condition [27]. The frequency of oscillation is taken such that the system is well within the Leidenfrost state,  . Finally, two reference particle-particle coefficients of restitution will be considered, r1 = 0.9 and
. Finally, two reference particle-particle coefficients of restitution will be considered, r1 = 0.9 and  , referred to as dissipative and quasi-elastic systems, respectively (the superscript denotes quantities for the quasi-elastic case). As we want to compare systems with similar packing fractions, in the quasi-elastic case we consider a larger number of particles, so that F1 = 12 and
, referred to as dissipative and quasi-elastic systems, respectively (the superscript denotes quantities for the quasi-elastic case). As we want to compare systems with similar packing fractions, in the quasi-elastic case we consider a larger number of particles, so that F1 = 12 and  .
.
5.1. Results
Time-averaged macroscopic fields are seen to converge as 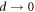 . A snapshot of the system configuration for three different particle sizes is shown in figure 1, where the significant difference in particle numbers can be directly recognized. Vertical profiles of the time-averaged packing fraction
. A snapshot of the system configuration for three different particle sizes is shown in figure 1, where the significant difference in particle numbers can be directly recognized. Vertical profiles of the time-averaged packing fraction  and the squared velocity fluctuations
and the squared velocity fluctuations  are shown in figure 2 for several different
are shown in figure 2 for several different  . The characteristics of the Leidenfrost state can be readily recognized: low density, high temperature regions near the bottom, below high density, low temperature regions higher up [22]. As expected from (7)–(8), only for small d the conserved fields converge, although convergence is fast enough to allow us to fabricate equivalent systems with a difference of more than four orders of magnitude in N/l2. The gaseous region (close to the bottom boundary) presents the most significant differences, although the maximum of
. The characteristics of the Leidenfrost state can be readily recognized: low density, high temperature regions near the bottom, below high density, low temperature regions higher up [22]. As expected from (7)–(8), only for small d the conserved fields converge, although convergence is fast enough to allow us to fabricate equivalent systems with a difference of more than four orders of magnitude in N/l2. The gaseous region (close to the bottom boundary) presents the most significant differences, although the maximum of 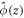 also decreases slightly as
also decreases slightly as  . Variations in the gaseous region are also significant in
. Variations in the gaseous region are also significant in  , which presents a threefold increase accompanied by a rising total temperature
, which presents a threefold increase accompanied by a rising total temperature  as
as  .
.
Figure 1. Configurations of macroscopically equivalent systems in the Leidenfrost state, for particle diameters d = 0.25, d = 0.5 and d = 1.0 from left to right. Notice that to improve the visualization here the base area has not been scaled with d, with the configuration repeated through the boundary conditions.
Download figure:
Standard image High-resolution imageFigure 2. Time-averaged vertical packing fraction profiles 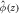 and velocity fluctuations profiles
and velocity fluctuations profiles  , for systems shown in the dissipative (r1 = 0.9, left) and quasi-elastic (r1 = 0.99, right) cases.
, for systems shown in the dissipative (r1 = 0.9, left) and quasi-elastic (r1 = 0.99, right) cases.
Download figure:
Standard image High-resolution imageThe shapes of  and
and  suggest that an additional source of disagreement comes from finite-size effects. The free-volume near the bottom wall, of course not taken into account in (7)–(8), is proportional to d, leading to significant differences for large d (see figure 2(a)). Secondly, variations of the convergent macroscopic fields can become comparable to d for large particles; notice for example that in the convergent
suggest that an additional source of disagreement comes from finite-size effects. The free-volume near the bottom wall, of course not taken into account in (7)–(8), is proportional to d, leading to significant differences for large d (see figure 2(a)). Secondly, variations of the convergent macroscopic fields can become comparable to d for large particles; notice for example that in the convergent  (in figure 2(a)), the height of the gaseous region
(in figure 2(a)), the height of the gaseous region  , which corresponds to only
, which corresponds to only 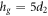 . In other words, the scalings fail when there is no clear separation of scales.
. In other words, the scalings fail when there is no clear separation of scales.
Beyond finite-size effects, the value of the coefficient of restitution is expected to have a significant influence, as we have taken 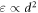 , indirectly affecting all transport coefficients. Indeed, quasi-elastic systems show a much higher agreement as d is varied, as shown in figure 2 by
, indirectly affecting all transport coefficients. Indeed, quasi-elastic systems show a much higher agreement as d is varied, as shown in figure 2 by  and
and  . The most significant differences are again observed near z = 0, further suggesting that these are finite-size, boundary-layer effects.
. The most significant differences are again observed near z = 0, further suggesting that these are finite-size, boundary-layer effects.
The sources of disagreement can be traced by measuring each term of equations (7)–(8) separately. For the energy-density dissipation rate, equation (8) states that I scales inversely linear with d, but simulation measurements show a considerable deviation in the range of d studied, as shown in figure 3(a). In dissipative systems variations are more than ∼50%, while in quasi-elastic systems it is only ∼15%. Nevertheless, a convergent behaviour is observed, and deviations between N/l2 ≈ 800 and N/l2 ≈ 50000 are already less than 3% in both cases. The general improvement for higher r suggests that the differences stem from neglecting higher order ε dependencies of the transport coefficients.
Figure 3. (a) Average total energy dissipation 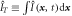 normalized by d, for dissipative (blue) and quasi-elastic (red) systems from figure 2. (b) Average total fluctuating velocity squared
normalized by d, for dissipative (blue) and quasi-elastic (red) systems from figure 2. (b) Average total fluctuating velocity squared  for the same systems as in (a). (c) Ratio of the two previous quantities
for the same systems as in (a). (c) Ratio of the two previous quantities  .
.
Download figure:
Standard image High-resolution imageDeviations from the expected d-invariant behaviour of T* are even stronger, especially in the dissipative case, as shown in figure 3(b) via  . But again a convergent behaviour is observed as
. But again a convergent behaviour is observed as  , and the quasi-elastic case shows a significant improvement. Interestingly, the dependency of
, and the quasi-elastic case shows a significant improvement. Interestingly, the dependency of  with d changes between dissipative and quasi-elastic systems: in the former case it increase monotonically as
with d changes between dissipative and quasi-elastic systems: in the former case it increase monotonically as  , while in the latter there is a slight overall decrease as d diminishes. The observed convergence to a macroscopic state, even when the individual scaling relations are seen to deviate, may be explained by the convergence of the general equations (1)–(3) to the perfect fluid equations.
, while in the latter there is a slight overall decrease as d diminishes. The observed convergence to a macroscopic state, even when the individual scaling relations are seen to deviate, may be explained by the convergence of the general equations (1)–(3) to the perfect fluid equations.
5.2. Low-frequency oscillations
Shaken beds of grains in density inverted states undergo collective semi-periodic oscillations, referred to as low-frequency oscillations (LFOs) [15, 23, 28, 29]. These are clearly identifiable in all simulations, making it possible to study their properties in equivalent macroscopic systems with different N. Their characteristic amplitude, quantified by the standard deviation of the evolution of the vertical centre of mass,  , is seen to be proportional to
, is seen to be proportional to  (
( ), as shown in figure 4(a). On the other hand, the characteristic frequency
), as shown in figure 4(a). On the other hand, the characteristic frequency  , obtained from the fast Fourier transform of zcm(t), converges to a finite value as
, obtained from the fast Fourier transform of zcm(t), converges to a finite value as  (
( ), as shown in figure 4(b). The
), as shown in figure 4(b). The ![${\left[{\omega }_{{LFO}}\right]}_{d}={d}^{0}$](https://content.cld.iop.org/journals/2399-6528/3/3/035006/revision2/jpcoab034aieqn120.gif) behaviour for large N is in accordance with a previously derived theoretical expression [23], where disregarding higher order effects, the characteristic frequency was found to be given by
behaviour for large N is in accordance with a previously derived theoretical expression [23], where disregarding higher order effects, the characteristic frequency was found to be given by  with ρg the density of the gaseous region and ms the total mass of the solid region.
with ρg the density of the gaseous region and ms the total mass of the solid region.  is thus expected to become d-invariant, as
is thus expected to become d-invariant, as  converges for
converges for  and both ρg and ms are macroscopic quantities determined by
and both ρg and ms are macroscopic quantities determined by  .
.
Figure 4. (a) Amplitude of the low-frequency oscillations 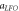 , defined as the standard deviation of the centre of mass
, defined as the standard deviation of the centre of mass  , for equivalent
, for equivalent  . In black, square root fit. (b) Frequency of oscillation of the column,
. In black, square root fit. (b) Frequency of oscillation of the column,  , for the same systems as in (a).
, for the same systems as in (a).
Download figure:
Standard image High-resolution imageFrom the decrease of  we can conclude that, in the limit of
we can conclude that, in the limit of  , LFOs would be unmeasurable, making it an essentially finite-number (granular) phenomena. Moreover, the
, LFOs would be unmeasurable, making it an essentially finite-number (granular) phenomena. Moreover, the  law suggests that low-frequency oscillations are driven by intrinsic fluctuations due to the low number of particles in the system. We propose the following interpretation: for small N, the momentum fluctuations given by particles of the gaseous phase hitting the solid/fluid phase is comparable to the overall momentum of the solid phase, and as such the amplitude of the oscillations are large. On the contrary, for larger N, a significant amount of particles in the gaseous phase would have to transfer momentum to the solid phase at the same time to have an equivalent impact, a situation that becomes increasingly improbable as N increases.
law suggests that low-frequency oscillations are driven by intrinsic fluctuations due to the low number of particles in the system. We propose the following interpretation: for small N, the momentum fluctuations given by particles of the gaseous phase hitting the solid/fluid phase is comparable to the overall momentum of the solid phase, and as such the amplitude of the oscillations are large. On the contrary, for larger N, a significant amount of particles in the gaseous phase would have to transfer momentum to the solid phase at the same time to have an equivalent impact, a situation that becomes increasingly improbable as N increases.
It is interesting to notice that even though the amplitude of LFOs becomes negligible as N increases, the mode is still present in the macroscopic system, as the ![${\left[{\omega }_{{LFO}}\right]}_{d}\approx {d}^{0}$](https://content.cld.iop.org/journals/2399-6528/3/3/035006/revision2/jpcoab034aieqn133.gif) behaviour shows. This further suggests that LFOs are an intrinsic characteristic of density inverted states, as argued in [23, 29]. The situation is curious, as the mode is a macroscopic phenomenon, but its amplitude is driven by microscopic effects. That is, the timescale to obtain invariant macroscopic fields,
behaviour shows. This further suggests that LFOs are an intrinsic characteristic of density inverted states, as argued in [23, 29]. The situation is curious, as the mode is a macroscopic phenomenon, but its amplitude is driven by microscopic effects. That is, the timescale to obtain invariant macroscopic fields,  , is independent of the length scale of averaging d. Furthermore, the evolution of zcm(t) is seen to become less chaotic and closer to a harmonic oscillation with a clearly defined frequency as
, is independent of the length scale of averaging d. Furthermore, the evolution of zcm(t) is seen to become less chaotic and closer to a harmonic oscillation with a clearly defined frequency as  , as increasingly steep peaks in the Fourier transforms indicate (not shown) [29]; this is another sign that low-frequency oscillations are driven by finite-number fluctuations.
, as increasingly steep peaks in the Fourier transforms indicate (not shown) [29]; this is another sign that low-frequency oscillations are driven by finite-number fluctuations.
6. Conclusions
We have studied the possibility of creating macroscopically equivalent granular systems in the same volume with significantly different numbers of particles N, by varying their size d. Considering the granular hydrodynamic equations, we have demonstrated that it is not possible to obtain equivalent systems in the most general flow case, as different terms scale differently with the particle diameter d. Nevertheless, after appropriately scaling the restitution coefficient, the limit  becomes well defined and leads to a d-invariant set of conservation laws corresponding to those of a perfect fluid. As a consequence of the proper dissipation scaling, the steady-state, fluxless equations become d-invariant in the low-dissipation limit, and for small particle sizes, up to
becomes well defined and leads to a d-invariant set of conservation laws corresponding to those of a perfect fluid. As a consequence of the proper dissipation scaling, the steady-state, fluxless equations become d-invariant in the low-dissipation limit, and for small particle sizes, up to 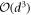 .
.
Simulations of perfect hard-spheres allowed us to test the derived scalings for a considerable range of total numbers of particles. As a test case we considered the granular Leidenfrost state, which was seen to converge to a limit time-averaged macroscopic state as  , with the convergence considerably faster for lower energy dissipation. Furthermore, the collective oscillatory behavior (LFO) present in the granular Leidenfrost state was deduced to be driven by the statistical fluctuations in systems with lower numbers of particles. This follows from the decrease of the amplitude of the oscillations with d for macroscopically equivalent systems. Moreover, the frequency of the LFOs remains approximately constant in the range of d studied, in accordance with previous results predicting a dependency only on macroscopic quantities.
, with the convergence considerably faster for lower energy dissipation. Furthermore, the collective oscillatory behavior (LFO) present in the granular Leidenfrost state was deduced to be driven by the statistical fluctuations in systems with lower numbers of particles. This follows from the decrease of the amplitude of the oscillations with d for macroscopically equivalent systems. Moreover, the frequency of the LFOs remains approximately constant in the range of d studied, in accordance with previous results predicting a dependency only on macroscopic quantities.
As a final comment, we would like to remark that the same framework could be used for the study of other non-equilibrium steady states in granular matter. Macroscopic convergence can be expected for different N, opening the possibility of studying macroscopically equivalent particle systems with significantly different numbers of particles, which could, for example, help in the up-scaling of simulations to regions relevant in industries.
Acknowledgments
NR and SL acknowledge support from the NWO-STW VICI grant number 10828. NR also acknowledges support from the Millennium Nucleus 'Physics of active matter' of the Millennium Scientific Initiative of the Ministry of Economy, Development and Tourism (Chile).
Footnotes
- 5
I.e., the constant that relates the granular temperature scale to the kinetic energy per particle.





