Analytical Uncertainty Evaluation of Material Parameter Measurements at THz Frequencies

Abstract

Material parameter extraction algorithms are studied and simplified both for transmission-reflection and transmission-only methods. The simplified relations, which are closed-form in some cases, are analyzed to establish the uncertainty sensitivity coefficients and therefore, to clarify the main uncertainty contributions and reduce the systematic and random errors. Simple closed-form expressions presented in this paper show the sensitivity of the extracted permittivity to each input parameter such as S₂₁ (phase and amplitude), frequency, and the material thickness. Results are presented for several material slabs for three waveguide frequency ranges 75–110 GHz, 140–220 GHz, and 500–750 GHz using VNA-based free-space technique in the THz domain. Comparison of results (and the associated uncertainties) between different algorithms can help to choose the optimal one suitable for lossy or low-loss materials, and thin or thicker slabs. This can explain why the same set of S-parameters data usually gives different final results (permittivity and permeability) with different algorithms and verify the reliability of the calibration and extraction process.

1 Introduction

Measurement of complex permittivity and permeability is very important in THz and millimeter-wave technology (substrates and dielectric components), biomedical and space applications, material engineering, and others. There exist different measurement techniques for different frequency ranges and materials which can cover lossy to low-loss slabs with various sizes and thicknesses [1]. Closed and open transmission cells and waveguides [2] or resonant cavities [3] are usually used in the microwave region. Waveguide or cavity methods, however, seem to be less applicable in the mm-Wave/THz domain because of mechanical problems and dimensional restrictions. Free-space non-contact methods are therefore used largely at these frequencies [4, 5]. Laser-based optical techniques have been, for a long time, the only solution for THz spectroscopy [6, 7], but recent progress in high-frequency semiconductor technology made available electronic-based components in the THz domain. Works [8, 9] discuss fundamental problems in reliable data analysis with known measurement uncertainty. A vector network analyzer (VNA) can be used as the core measurement unit with quasi-optical associated devices to set the free-space non-contact measurements up. The setup has to be adequately calibrated to derive S-parameters on the surface of the material-under-test (MUT) [4]. Monte Carlo simulation is also used to evaluate the measurement uncertainty of the VNA [10]. Based on the measured S-parameters and the MUT thickness and positioning, the permittivity and permeability can be extracted.

Material parameter extraction methods are based on reflection [11] and transmission parameters (or only one of them [1, 12, 13]). The algorithms usually suffer from instability or complicated iterative process and use genetic algorithms [14] or other numerical/optimization techniques [1, 12, 13, 15]. Also some methods require certain a priori knowledge of the material [4, 12, 16]. It is often observed that with the same set of S-parameters data, the extracted permittivity and permeability are not the same with different algorithms and therefore, the reliability of the full process of the material characterization gets questioned. We believe that the best solution here is the “sensitivity analysis” of the extraction methods. The abovementioned classic algorithms and many others are usually complicated and the sensitivity/error analysis may need a more complicated numerical process. By establishing reliable simplified (mostly closed-form expressions) extraction models, we will be able to show the sensitivity in a comprehensive and clear manner. The “simplification” and “sensitivity analysis” are the key points and main novelties of this work.

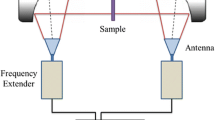
This paper presents simplified relations for both transmission-reflection (Section 2) and transmission-only (Section 3) methods with analytical closed-form expressions of uncertainty sensitivity coefficients. Measurement results are based on non-contact free-space techniques by using VNA and the associated frequency extensions for the bands 75–110 GHz, 140–220 GHz, and 500–750 GHz. Non-magnetic materials with relative permeability μ_r = 1 are assumed in this paper. The quasi-optical device here is a commercially available mode-convertor (Swissto12@ MCK [17, 18] set of two corrugated horn antennas). The system is supposed to convert waveguide propagation modes to TEM free-space mode on its aperture where the MUT is installed. We have been working on the setup optimization and in-depth study of its electromagnetic characteristics (propagation modes, matching, losses, aperture/gap scattering, etc.) and the system calibration. The study of the setup and its optimization is mainly based on theoretical and experimental works of [19, 20]. This paper is focused on extraction methods, only, whereas both the VNA calibration and the associated frequency extender optimization are performed to minimize the uncertainties of the input parameters (S₂₁, amplitude, and phase).

The results are presented at higher frequencies and in the mm-Wave/THz domain, but we believe the methods and analysis process presented here can be used for other frequency ranges and therefore helpful for the microwave and THz community, in general.

2 Transmission/Reflection Method

Reflection (S₁₁, S₂₂) and transmission (S₂₁, S₁₂) data can be processed to obtain real and imaginary parts of both permittivity ε = ε₀ε_r and permeability μ = μ₀μ_r of the MUT (the relative permittivity is expressed as $\varepsilon _{r} = {\varepsilon }_{r}^{\prime } - {\text {j}} {\varepsilon }_{r}^{\prime \prime }$). Various iterative and non-iterative algorithms have been presented for this goal [1, 12, 21]. The classic Nicolson-Ross-Weir (NRW) method [1] deals with Γ and T (T is the transmission coefficient and Γ is the reflection coefficient) to extract μ and ε, simultaneously. The method gives unstable results for low-loss and high-refractive materials when $S_{11} \sim 0$ and $\left | S_{21} \right | \sim 1$ at specific frequencies

$$ S_{11} = \frac{{{\varGamma} \left( {1 - T^{2} } \right)}}{{1 - {\varGamma}^{2} T^{2} }}, $$

(1)

$$ S_{21} = \frac{{T\left( {1 - {\varGamma}^{2} } \right)}}{{1 - {\varGamma}^{2} T^{2} }}, $$

(2)

$$ {\varGamma} = X \pm \left( {\sqrt {X^{2} - 1} } \right){\text{~~and~~}}\frac{{\varepsilon_{r} }}{{\mu_{r} }} = \left( {\frac{{1 - {\varGamma} }}{{1 + {\varGamma} }}} \right)^{2}, $$

(3)

where

$$ X = \frac{{{S}_{11}^{2} - {S}_{21}^{2} + 1}}{{2S_{11} }}, $$

(4)

$$ T = e^{- j\frac{\omega }{c}d\sqrt {\mu_{r} \varepsilon_{r} } }, $$

(5)

and d is the material slab thickness, c is the free-space speed of light, and ω is the angular frequency. A comprehensive method has been presented [22] to correct the instability. Using the classic (1), (2), and (3) to simplify the final relations relevant to ε and μ as a closed-form formula, we obtain

$$ \frac{{\varepsilon_{r} }}{{\mu_{r} }} = \left( {\frac{{1 - {\varGamma} }}{{1 + {\varGamma} }}} \right)^{2} = \left( {\frac{{\left( {1 - X} \right) \mp \sqrt {X^{2} - 1} }}{{\left( {1 + X} \right) \pm \sqrt {X^{2} - 1} }}} \right)^{2} . $$

(6)

The expansion of Eq. 6 leads to

$$ \frac{{\varepsilon_{r} }}{{\mu_{r} }} = \frac{{\left( {X - 1} \right)\left( {X \pm \sqrt {X^{2} - 1} } \right)}}{{\left( {X + 1} \right)\left( {X \pm \sqrt {X^{2} - 1} } \right)}} $$

(7)

$$ \frac{{\varepsilon_{r} }}{{\mu_{r} }} = \frac{{X - 1}}{{X + 1}} = \frac{{\left( {S_{11} - 1} \right)^{2} - S_{21}^{2} }}{{\left( {S_{11} + 1} \right)^{2} - S_{21}^{2} }}. $$

(8)

The material extraction method using Eq. 8 is independent of the material thickness (i.e., the material thickness d is not a variable here and the extraction process is not affected by improper input data d) and can give reliable and stable results if S₁₁ is not very small. For some materials, e.g., body tissue or substrates for wearable antennas, the thickness d is difficult to measure precisely. Yet, the instability problems appear for low-loss materials when $S_{11} \sim 0$ and $\left | S_{21} \right | \sim 1$ at specific frequencies which is equivalent to the classic NRW method [1, 21]. Similar relations have been already used to determine the impedance of transmission lines with dielectric-filled sections [24].

Closed-form Eq. 8 provides a more comprehensive analysis of the uncertainties with a clear contribution of each measured S-parameter. By applying the partial derivatives of Eq. 8, sensitivity coefficients of ε_r can be derived as a function of S₁₁ and S₂₁. Simple and closed-form structure of Eq. 8 makes its derivatives closed-form, as well

$$ \frac{{\partial \varepsilon_{r} }}{{\partial S_{11} }} = \frac{{4\left( {S_{11}^{2} + S_{21}^{2} - 1} \right)}}{{\left[ {\left( {S_{11} + 1} \right)^{2} - S_{21}^{2} } \right]^{2} }}, $$

(9)

$$ \frac{{\partial \varepsilon_{r} }}{{\partial S_{21} }} = \frac{{ - 8S_{11} S_{21} }}{{\left[ {\left( {S_{11} + 1} \right)^{2} - S_{21}^{2} } \right]^{2} }}. $$

(10)

Figure 1 shows the sensitivity coefficients of the permittivity for a 3-mm Plexiglass slab. As shown, for both S₁₁ and S₂₁, there are nearly simultaneous minimum sensitivity points which are in agreement with the results of “instability corrected” curves in [22]. Given nominal $\left | {\varDelta } S_{11} \right |$ and $\left | {\varDelta } S_{21} \right |$ approximately 0.015 (the overall measurement uncertainty of S₁₁ and S₂₁ due to repeatability, VNA stability, noise, drift, etc.), the associated uncertainty of $\left | \varepsilon _{r} \right |$ is estimated around 0.1 ($\sim$ 4%, relative) when ${\varepsilon }_{r}^{\prime }$ = 2.6. Therefore, the simple closed-form (yet unstable) relation (8) can give reliable results with calculable uncertainties around the frequencies 140 GHz, 170 GHz, and 200 GHz (Fig. 1).

Fig. 1

A 3-mm plexiglass slab, sensitivity coefficients of ε_r (140–220 GHz): unstable real part of ε_r (blue), and sensitivity coefficients of S₁₁ (9) and S₂₁ (10)

Figure 2 shows the sensitivity coefficients of the permittivity for a high-refractive low-loss 1.2-mm sample YZrO₂. As shown, for both the S₁₁ and S₂₁, there are nearly simultaneous minimum sensitivity points. In this case, the $\left | {\varDelta } S_{11} \right |$ and $\left | {\varDelta } S_{21} \right |$ are approximately 0.015, and the associated uncertainty of $\left | \varepsilon _{r} \right |$ is estimated around 7% when ${\varepsilon }_{r}^{\prime }$ = 33.7. The best uncertainties are observed at the frequency points around 157 GHz, 179 GHz, 201 GHz, and 220 GHz (Fig. 2). The minima and maxima of the uncertainty can be explained by analysis of the denominator of Eqs. 9 and 10. The uncertainty is minimal when the $\left | S_{21} \right |$ is minimal and the $\left | S_{11} \right |$ is maximal and vice versa.

Fig. 2

A 1.2-mm YZrO₂ slab, sensitivity coefficients of ε_r (140–220 GHz): unstable real part of ε_r (blue), and sensitivity coefficients of S₁₁ and S₂₁

Comparing with the results of Fig. 1, we can see the relative uncertainty is higher and this shows the difficulties of extracting parameters for high-refractive thin materials with the transmission-reflection method. To demonstrate these challenges, we have calculated the permittivity (real and imaginary parts) of the same sample of Fig. 2 with two well-known extraction methods: stable non-iterative [21] and NIST-iterative [12] (Fig. 3). METAS VNA-Tools II [25] has been used to show the extracted material parameters with classic methods. VNA-Tools II is a metrology software to compute uncertainties of the measured S-parameters with various post-processing features including material parameter extraction with associated uncertainties.

Fig. 3

A 1.2-mm YZrO₂ slab, 140–220 GHz: ${\varepsilon }_{r}^{\prime }$ (top) and ${\varepsilon }_{r}^{\prime \prime }$ (bottom), with two well-known classic methods, NIST (black) and stable non-iterative (red). The methods show diverged results and partially “unphysical” for ${\varepsilon }_{r}^{\prime \prime }$

As shown in Fig. 3, the real part of ${\varepsilon }_{r}^{\prime }$ varies between 33.5 and 34 and the results of imaginary part ${\varepsilon }_{r}^{\prime \prime }$ are much more deviated or even meaningless for some frequencies. In the next section dedicated to the transmission-only method, we show how we can find more reliable extracted parameters by simplifying the algorithm and analyzing the associated uncertainties.

Here at the end of Section 2, we will show an original application of the simple closed-form formula (8) and its partial derivatives (9), (10) [22]. Actually, reliable results of ${\varepsilon }_{r}^{\prime }$ (real part) even for a limited number of points in a given frequency range are of interest. Most of the “normal” homogeneous materials have nearly constant ε_r in the mm-Wave/sub-THz domain. Besides, the calculation of ε_r and its associated uncertainties is independent of the slab thickness. The thickness of the slab and its positioning can be one of the major uncertainty contributions (cause a systematic error) in reflection-and-transmission methods [26] and transmission-only methods [9], as well.

As mentioned, closed-form Eq. 8 is independent of the slab’s thickness and can correct the systematic errors caused by this sensitive parameter. Figure 4 shows the high sensitivity of the extracted ${\varepsilon }_{r}^{\prime }$ (real part) of a 2-mm (nominal thickness) fused silica slab.

Fig. 4

A 2-mm fused silica (F.Si) slab, ${\varepsilon }_{r}^{\prime }$, and sensitivity coefficients of ε_r (140–220 GHz). Extracted ${\varepsilon }_{r}^{\prime }$ with thicknesses 2.00 mm (top), 2.04 mm (middle), and 2.07 mm (bottom). Non-iterative stable method (black) and Eq. 8 (red) are used, optimal match (${\varepsilon }_{r}^{\prime }$ = 3.8) with 2.07 mm thickness at the “best” uncertainty points $\sim$ 167 GHz and $\sim$ 205 GHz

The parameter extracted by the non-iterative stable method [21] varies about 5%, which is a considerable systematic error. This is regarding ${\varepsilon }_{r}^{\prime }$ = 4.05 (for nominal 2 mm thickness), to ${\varepsilon }_{r}^{\prime }$ = 3.9 (2.04 mm thickness, measured with high-precision mechanical devices) and finally ${\varepsilon }_{r}^{\prime }$ = 3.8 (for 2.07 mm thickness, which gives reasonable match to Eq. 8 at the best uncertainty points $\sim$ 167 GHz and $\sim$ 205 GHz).

It can be shown that the ε_r uncertainty minimum points occur when the measured $\left | S_{11} \right |$ and $\left | S_{21} \right |$ reach their maximum and minimum (Fabry-Perot multiple reflection inside the slab), consequently. This fact may still make the extraction and uncertainty evaluation process easier.

Measurement of reflection parameters using a VNA is problematic at higher frequencies, because of the lack of suitable short standard and positioning challenges [4] with micrometer precision. The short standard must be perfectly conducting and ideally reflective (i.e., polished), which is not easy at sub-millimetre frequencies. The positioning (straightness and tilt, exact and repeatable position) is crucial especially for the measurement of the S₁₁ phase. For non-magnetic materials (μ_r = 1 −j0), the transmission-only method (the S₂₁ parameter, only) can be more reliable and easier in terms of setup calibration and parameter extraction. The $\left | {\varDelta } S_{11} \right |$ is usually bigger than $\left | {\varDelta } S_{21} \right |$ and the total uncertainty of the method using S₁₁ is then bigger (note that the sensitivity coefficients must be multiplied by the $\left | {\varDelta } S_{11} \right |$ or $\left | {\varDelta } S_{21} \right |$ to get the final measurement uncertainty).

3 Transmission-Only Method

The transmission-only method utilizes the S₂₁ (or S₁₂) parameter on the material slab to derive T and consequently, to extract the permittivity $\varepsilon _{r} = {\varepsilon }_{r}^{\prime } - j{\varepsilon }_{r}^{\prime \prime }$. Here T is a function of the material thickness d and its permittivity and permeability (5). For the materials which are not very lossy (${\varepsilon }_{r}^{\prime \prime } /{\varepsilon }_{r}^{\prime } = \tan \delta <$ 0.1), T can be separated directly to phase and magnitude parts [4]

$$ T = \exp \left( { - j\frac{{\omega d}}{c}\sqrt {{\varepsilon}_{r}^{\prime} } } \right)\exp \left( { - \frac{{\omega d}}{{2c\sqrt {{\varepsilon}_{r}^{\prime} } }}{\varepsilon}_{r}^{\prime\prime} } \right). $$

(11)

This means the phase and magnitude of T give real and imaginary parts of permittivity, consequently

$$ \phi \left( T \right) = - \frac{{\omega d}}{c}\sqrt {{\varepsilon}_{r}^{\prime} }, $$

(12)

$$ \ln \left| T \right| = - \frac{{\omega d}}{{2c\sqrt {{\varepsilon}_{r}^{\prime} } }}{\varepsilon}_{r}^{\prime\prime}. $$

(13)

Here, we suggest a very easy and original way to evaluate $\phi \left (T \right )$ from $\phi \left (S_{21} \right )$ which are related by the Fabry-Perot relation (2) with the unknown Γ.

3.1 Simple Expression for the Phase of T

First, we look in the phase of $\left ({1 - {\varGamma }^{2} } \right )$ in Eq. 2, if the material is not very lossy (${\varepsilon }_{r}^{\prime \prime } /{\varepsilon }_{r}^{\prime } = \tan \delta <$ 0.1). In this case, the phase is equal to zero with a very small error. Then, we search the points for which the phase of $\left ({1 - T^{2} {\varGamma }^{2} } \right )$ is zero. If $\phi \left ({T^{2} } \right ) = n\pi$ ($n \in \mathbb {Z}$), then $\phi \left ({1 - T^{2} {\varGamma }^{2} } \right ) = 0$ and

$$ \phi \left( T \right) = \phi \left( {S_{21} } \right) = n\pi /2. $$

(14)

In order to better understand (14), suppose that the phase $\phi \left (T \right )$ is equal to nπ/2, then calculate the phase $\phi \left ({S_{21} } \right )$ with the assumption of $\phi \left ({{\varGamma }^{2} } \right ) \approx 0$. This means at the points where the measured $\phi \left ({S_{21} } \right )$ is equal to nπ/2, the $\phi \left (T \right )$ has also the same value and therefore, the complicated equation (2) does not need to be solved and used as the extraction parameter basis. Figure 5 shows the phase of S₂₁ and T (approximated) for the material from Fig. 2 (1.2-mm YZrO₂ sample) and their equality at “nπ/2” points. In this figure, we have also calculated the real part of permittivity from Eq. 12 at the points where $\phi \left ({S_{21} } \right ) = n\pi$

$$ \phi \left( {S_{21} } \right) = n\pi = \phi \left( T \right) = - \frac{{\omega d}}{c}\sqrt {{\varepsilon}_{r}^{\prime} }. $$

(15)

Here, ${\varepsilon }_{r}^{\prime }$ is intentionally calculated only for “nπ” points rather all “nπ/2” points, as we will show later that at “nπ” points the uncertainty (sensitivity coefficient) is minimum in the transmission-only method. It can be shown that around “nπ” points the $\left | S_{21} \right |$ reaches its maximum (Fig. 5).

Fig. 5

A 1.2-mm YZrO₂ sample, 140–220 GHz: calculation of ${\varepsilon }_{r}^{\prime }$ at $\phi \left ({S_{21} } \right ) = n\pi = \phi \left (T \right )$ points (black solid line) and comparing with a non-perfect extraction (blue dashed-line)

Figure 5 shows the reliability of the simple method (14), (15) with a constant ${\varepsilon }_{r}^{\prime }$ = 33.7 comparing with Fig. 3 in which well-known classic methods are used. Once ${\varepsilon }_{r}^{\prime }$ is calculated at “nπ” points with minimum uncertainty, Γ² is calculated (by definition)

$$ {\varGamma}^{2} = \left| {\left( {\sqrt {{\varepsilon}_{r}^{\prime} } - 1} \right)/\left( {\sqrt {{\varepsilon}_{r}^{\prime} } + 1} \right)} \right|^{2}. $$

(16)

Note that the calculated Γ² in this step is a constant for the whole studied frequency range. Meanwhile, from Eq. 2, T will be determined (as a complex number for all the frequency points) with a quadratic relation where the condition $\left | T \right | < 1$ is imposed. The calculated T is the key for the extraction of permittivity from Eqs. 12 and 13.

To show the reliability of the simple method demonstrated in Eqs. 14 and 15, here we present an interesting and challenging case, i.e., results for a high-refractive low-loss 0.6-mm alumina slab in the 500–750-GHz band, for which the S-parameters are not time gated, see Fig. 6.

Fig. 6

A 0.6-mm alumina sample, 500–750 GHz: calculation of ${\varepsilon }_{r}^{\prime }$ at $\phi \left ({S_{21} } \right ) = n\pi = \phi \left (T \right )$ points (black solid line) and comparing with a non-perfect extraction (blue dashed-line)

In general spectroscopy, materials with peaks in the extracted permittivity (spectral fingerprint) show sharp changes both in the amplitude and phase of S₂₁ and are usually observed at higher THz frequencies, although some energetic materials exhibit peaks at frequencies below 500 GHz [23]. The material parameter extraction around these points may be directly based on S₂₁ phase and amplitude and then corrected for the Fabry-Perot effect and multiple reflections.

In the next part of this section, the sensitivity analysis of transmission-only equations will be presented to calculate real and imaginary parts of permittivity with estimations of associated uncertainties.

3.2 Uncertainty Analysis of the Transmission-Only Method

Partial derivative process on Eq. 2 gives sensitivity coefficients of T as a function of S₂₁

$$ \partial T = \frac{{\left( {1 - {\varGamma}^{2} T^{2} } \right)\partial S_{21} - 2T{\varGamma}^{2} S_{21} \partial T}}{{1 - {\varGamma}^{2} }} + \left( {\frac{{T - S_{21} T^{2} }}{{1 - {\varGamma}^{2} }}} \right)\partial {\varGamma}^{2}, $$

(17)

$$ \frac{{\partial T}}{{\partial S_{21} }} = \frac{T}{{S_{21} }}\frac{1}{{1 + S_{21} \frac{{2T{\varGamma}^{2} }}{{1 - {\varGamma}^{2} }}}} + \left( {\frac{{T - S_{21} T^{2} }}{{1 - {\varGamma}^{2} }}} \right)\frac{{\partial {\varGamma}^{2} }}{{\partial S_{21} }}. $$

(18)

At all the points and especially at “nπ” points, ∂Γ² is much smaller than ∂S₂₁ (and negligible); thus, Eq. 18 can be shortened as

$$ \frac{{\partial T}}{{\partial S_{21} }} = \frac{T}{{S_{21} }}\frac{1}{{1 + S_{21} \frac{{2T{\varGamma}^{2} }}{{1 - {\varGamma}^{2} }}}}, $$

(19)

$$ \frac{{\partial T}}{T} = \frac{{\partial S_{21} }}{{S_{21} }}\frac{1}{{1 + 2TS_{21} \frac{{{\varGamma}^{2} }}{{1 - {\varGamma}^{2} }}}}. $$

(20)

Now, by using closed-form equations for real and imaginary parts of permittivity (12), (13) and performing partial derivatives, the sensitivity coefficients are determined

$$ \begin{array}{l} \left( {\frac{{\omega d}}{{2c}}\sqrt {{\varepsilon}_{r}^{\prime} } } \right)\partial {\varepsilon}_{r}^{\prime\prime} = \frac{{\partial \left| T \right|}}{{\left| T \right|}} \leq \frac{{\left| \partial{S_{21} } \right|}}{{\left| {S_{21} } \right|}}\left| {\frac{1}{{1 + 2TS_{21} \frac{{{\varGamma}^{2} }}{{1 - {\varGamma}^{2} }}}}} \right| \\ \to {\text{~~~}}\frac{{\partial {\varepsilon}_{r}^{\prime\prime} }}{{\left| \partial{S_{21} } \right|}} \leq \frac{{2c}}{{\omega d\sqrt {{\varepsilon}_{r}^{\prime} } }}\left| {\frac{{1 - {\varGamma}^{2} }}{{S_{21} \left( {1 - {\varGamma}^{2} + 2TS_{21} {\varGamma}^{2} } \right)}}} \right| \end{array}, $$

(21)

$$ \frac{{\partial \sqrt {{\varepsilon}_{r}^{\prime} } }}{{\partial \phi \left( {S_{21} } \right)}} = \frac{c}{{2\pi fd}}\text{and}\frac{{\partial \sqrt {{\varepsilon}_{r}^{\prime} } }}{{\partial d}} = \phi \left( {S_{21} } \right) \frac{{c}}{{2\pi fd^{2} }}. $$

(22)

Equations 20, 21, and 22 show the uncertainties and sensitivity coefficient in simple closed-forms and as a clear function of the measured S₂₁, frequency f, and the sample thickness d.

Figure 7 shows ∂T/∂S₂₁ for the YZrO₂ sample with thickness 1.2 mm with the minimum sensitivities at the points where $\left | S_{21} \right |$ is maximum (i.e., “nπ” points of $\phi \left ({S_{21} } \right )$, the phase of S₂₁). These are the points where the imaginary part of ${\varepsilon }_{r}^{\prime \prime }$ has the minimum uncertainty and the real part of ${\varepsilon }_{r}^{\prime }$ is directly calculated from $\phi \left ({S_{21} } \right )$.

Fig. 7

A 1.2-mm YZrO₂ sample, 140–220 GHz: uncertainty sensitivity coefficient with transmission-only method (bottom) and calculation of ${\varepsilon }_{r}^{\prime \prime }$ with best uncertainties at $\phi \left ({S_{21} } \right ) = n\pi = \phi \left (T \right )$ points (top), and the best fit (black solid line) for the entire frequency range $0.13 < {\varepsilon }_{r}^{\prime \prime } < 0.17$

By comparing Figs. 5 and 7 and Fig. 3, the advantages of the simplified transmission-only equations, presented in this paper, and comprehensive uncertainty analysis can be demonstrated. Another set of results is presented in Fig. 8 for a thicker 3-mm plexiglass slab to compare simplified transmission-only method with well-known classic algorithms (NIST-iterative and stable non-iterative) based on transmission-reflection data. The S-parameters data in the 140–220 GHz range are time gated (smoothening) and have been provided from Swissto12@ [26]. They have been processed in this paper to compare different extraction algorithms and evaluate/analyze the uncertainties.

Fig. 8

A 3-mm plexiglass slab, 140–220 GHz: uncertainty sensitivity coefficient with transmission-only method (bottom, solid red curve is $\left | S_{21} \right |$, dashed blue curve is the sensitivity) and calculation of ${\varepsilon }_{r}^{\prime \prime }$ with best uncertainties at $\phi \left ({S_{21} } \right ) = n\pi = \phi \left (T \right )$ points (middle), the best fit (black solid line) for the entire frequency range $0.030 < {\varepsilon }_{r}^{\prime \prime } < 0.034$. Comparing with transmission-reflection method (top), where the well-known classic methods give diverged results $0.025 < {\varepsilon }_{r}^{\prime \prime } < 0.039$

This method needs to observe a couple of minima and maxima on the $\left | S_{21} \right |$ curves (“nπ/2” points of $\phi \left ({S_{21} } \right )$). This occurs if the material is not very thin (electrical length in the THz domain) and very low-refractive. Examples here can be an alumina slab (${\varepsilon }_{r}^{\prime }\sim 9.5$) with 1 mm thickness or more, and plexiglass (${\varepsilon }_{r}^{\prime }\sim 2.7$) thicker than 2 mm for the 75–110-GHz band. This can change to thin slabs, i.e., alumina with the thickness 0.2 mm and plexiglass with the thickness 0.4 mm (relevant to the electric-length) for the 500–750-GHz band.

Note that the S-parameters and their measurement uncertainty depend on the MUT conditions (positioning, surface quality), environmental conditions (VNA noise, drift, stability), VNA calibration and measurement repeatability, etc. Most of these influences can be demonstrated by $\left | {\varDelta } S_{11} \right |$ and $\left | {\varDelta } S_{21} \right |$. In this paper, we focused mostly on the material parameter extraction and the sensitivity coefficients.

3.3 More Results with the Simplified Transmission-Only Equations

We present more results for two other waveguide frequency ranges 75–110 GHz and 500–750 GHz with different types of material. Swissto12@ MCK (Fig. 9) is used and calibrated for transmission data S₂₁. For these measurements, it is chosen not to use time-gating option of the VNA in order to have a more clear perspective of the overall uncertainty budget.

Fig. 9

Measurement setup, MCK connected to the VNA frequency extension modules with the MUT clamped between the two antennas apertures

For the results here (Figs. 10, 11, 12, and 13), the estimated uncertainty for ${\varepsilon }_{r}^{\prime }$ is 3–4% and 10–15% for ${\varepsilon }_{r}^{\prime \prime }$. It depends on the material thickness d (as one of the most important contribution to the uncertainties ∂d/d), $\left | T \right |$, and other parameters in Eqs. 21 and 22.

Fig. 10

Plexiglass 3-mm sample, 500–750 GHz: ${\varepsilon }_{r}^{\prime }$ and ${\varepsilon }_{r}^{\prime \prime }$

Fig. 11

Float-glass 1.5 mm, 500–750 GHz: ${\varepsilon }_{r}^{\prime }$ and ${\varepsilon }_{r}^{\prime \prime }$

Fig. 12

Manufactured lossy material, 4 mm sample, 75–110 GHz: ${\varepsilon }_{r}^{\prime }$ and ${\varepsilon }_{r}^{\prime \prime }$

Fig. 13

Manufactured lossy material, 2-mm sample, 500–750 GHz: ${\varepsilon }_{r}^{\prime }$ and ${\varepsilon }_{r}^{\prime \prime }$

Figure 13 shows an interesting behavior of (manufactured) high-loss materials in THz domain for which the real part of permittivity decreases with frequency.

4 Conclusion

Transmission-reflection and transmission-only methods have been studied and reviewed. Simplified closed-form equations are presented to correct the systematic errors and analyze the uncertainty sensitivity coefficients in material parameter extraction. Various materials (low-loss, high-refractive, lossy, thin, and thick) are measured in THz domain for three waveguide frequency ranges: 75–110 GHz, 140–220 GHz, and 500–750 GHz. The presented method helps to understand the uncertainty (and reduce it) and the reliability of the relevant algorithms.

It is interesting to mention that the “sensitivity” curves of transmission-reflection method and transmission-only method give minimum uncertainty at different points (often opposite, regarding the maximum and minimum points of $\left | S_{21} \right |$). This may help to consider combined methods to reduce the uncertainties at wider frequency bands.