Conditions for the Stable Acceleration of Ion Rings by Collapsed Liners

Abstract

The conditions of suppressing the collective slowing-down of an ionic beam on electrons, which is caused by the excitation of electron plasma oscillations (beam instability) by ions, are found. In contrast to available explicit and implicit indications, a large spread of the energies only in an ionic beam is insufficient for this suppression. The acceleration of ions is shown to become stable when a sufficiently large spread of the electron velocities is simultaneously present. The beam instability of ions is suppressed by the Landau damping of the ion-excited plasma waves at electrons. The results obtained are used to analyze the possibility of ion acceleration by collapsed cylindrical plasma liners.

DERIVATION OF EQUATION (6)

Let the electric field of the wave excited by ions in plasma be E(r, t). The last term in the electrodynamic formula

$${\mathbf{E}} = - \nabla \varphi - \frac{1}{c}\frac{{\partial {\mathbf{A}}}}{{\partial t}}$$

is neglected, since we are interested in plasma with nonrelativistic particles. Therefore, this field is potential,

$${\mathbf{E}} \approx - \nabla \varphi .$$

(13)

We first consider a cloud of “cold” electrons (for definiteness, we now speak only about them), the velocity of which at arbitrary point r at time t has a certain value, v(r, t). This cloud is described a distribution function f(r, V, t) = n(r, t)δ[V – v(r, t)]. In this case, the kinetic description of the behavior of the cloud that is based on the Vlasov equation (collisions are neglected) is equivalent to the hydrodynamic description [17, 18].

Let the cloud be at rest at t = 0. At t > 0, it begins to move under the action of the electric field of the wave,

$$\begin{gathered} {\mathbf{E}} = {{{\mathbf{E}}}_{0}}\cos ({\mathbf{k}} \cdot {\mathbf{r}} - \omega t) \\ = \operatorname{Re} ({{{\mathbf{E}}}_{0}}{{e}^{{i{\mathbf{k}} \cdot {\mathbf{r}} - i\omega t}}}) = \operatorname{Re} ( - i{\mathbf{k}}\varphi ) \\ \end{gathered} $$

according to the law

$${\mathbf{\dot {v}}} = \frac{q}{m}\left( {{\mathbf{E}} + \frac{1}{c}{\mathbf{v}} \times {\mathbf{B}}} \right),$$

(14)

which coincides with the equation of motion of one particle, which is a consequence of the linearization of the hydrodynamic Euler equation. Here, we neglect the action of the magnetic field of the wave on electrons, since it is low as compared to the main magnetic field in plasma B, along which axis z is directed. Solution (14) written in a complex form is

$$\left\{ \begin{gathered} {{{v}}_{x}} = - \frac{{iq(i\omega {{k}_{x}} + {{\omega }_{{{\text{Be}}}}}{{k}_{y}})}}{{m({{\omega }^{2}} - \omega _{{{\text{Be}}}}^{2})}}\varphi , \hfill \\ {{{v}}_{y}} = - \frac{{iq(i\omega {{k}_{y}} - {{\omega }_{{{\text{Be}}}}}{{k}_{x}})}}{{m({{\omega }^{2}} - \omega _{{{\text{Be}}}}^{2})}}\varphi , \hfill \\ {{{v}}_{z}} = \frac{{q{{k}_{z}}}}{{m\omega }}\varphi . \hfill \\ \end{gathered} \right.$$

(15)

The bulk electron density is n = n₀ + n₁. Here, n₁(r, t) is its weak perturbation induced by the wave, |n₁| ≪ n₀. This quantity is found from the continuity equation ∂n/∂t + ∇ ⋅ (nv)= 0. After the linearization of this equation, we have

$${{n}_{1}} = {{n}_{0}}\frac{{{\mathbf{k}} \cdot {\mathbf{v}}}}{\omega }.$$

(16)

Using Eqs. (15) and (16), we obtain the following expression for the perturbation of the electron charge density:

$${{\rho }_{{\text{e}}}} = q{{n}_{1}} = \frac{{\omega _{{\text{e}}}^{2}{{k}^{2}}}}{{4\pi }}\left( {\frac{{{{{\sin }}^{2}}\theta }}{{{{\omega }^{2}} - \omega _{{{\text{Be}}}}^{2}}} + \frac{{{{{\cos }}^{2}}\theta }}{{{{\omega }^{2}}}}} \right)\varphi ,$$

(17)

where θ is the angle between vectors k and B.

As noted above, Eq. (17) belongs to frame of reference K where particles are at rest at t = 0. If the particles move at velocity v, we have to pass to frame of reference K ', which moves with respect to K at velocity v. In the latter, the particles were at rest at t = 0; therefore, we can apply Eq. (17) to it by substituting ω' = ω – k ⋅ v for ω. Indeed, the coordinates in both reference systems are related by the formula r = r' + vt. The electric field in the wave oscillates according to the law

$$\begin{gathered} \exp (i{\mathbf{k}} \cdot {\mathbf{r}} - i\omega t) = \exp [i{\mathbf{k}} \cdot ({\mathbf{r}}{\kern 1pt} '\, + {\mathbf{v}}t) - i\omega t] \\ = \exp (i{\mathbf{k}} \cdot {\mathbf{r}}{\kern 1pt} '\, - i\omega {\kern 1pt} '{\kern 1pt} t), \\ \end{gathered} $$

therefore, the oscillation frequency in system K ' is ω'. Thus, Eq. (17) is rewritten in the form

$${{\rho }_{{\text{e}}}} = \frac{{\omega _{{\text{e}}}^{2}{{k}^{2}}}}{{4\pi }}g(\omega - {\mathbf{k}} \cdot {\mathbf{v}})\varphi ,$$

where

$$g(\omega - {\mathbf{k}} \cdot {\mathbf{v}}) = \frac{{{{{\sin }}^{2}}\theta }}{{{{{(\omega - {\mathbf{k}} \cdot {\mathbf{v}})}}^{2}} - \omega _{{{\text{Be}}}}^{2}}} + \frac{{{{{\cos }}^{2}}\theta }}{{{{{(\omega - {\mathbf{k}} \cdot {\mathbf{v}})}}^{2}}}}.$$

Let electrons consist of groups A moving at velocities v_A and having densities n_A. Then, we have

$$\begin{gathered} {{\rho }_{{\text{e}}}} = \sum\limits_A^{} {\rho _{{\text{e}}}^{A} = \varphi \sum\limits_A^{} {\frac{{{{{(\omega _{{\text{e}}}^{A})}}^{2}}{{k}^{2}}}}{{4\pi }}g(\omega - {\mathbf{k}} \cdot {{{\mathbf{v}}}_{A}})} } \\ = \frac{{\omega _{{\text{e}}}^{2}{{k}^{2}}}}{{4\pi }}\varphi \sum\limits_A^{} {{{\xi }_{A}}g(\omega - {\mathbf{k}} \cdot {{{\mathbf{v}}}_{A}}),} \\ \end{gathered} $$

(18)

where ξ_A = n_A/n₀ is the fraction of electrons that belong to group A and n₀ = $\sum\nolimits_A^{} {{{n}_{A}}}$ is the total electron density. In the case of a continuous velocity distribution, instead of Eq. (18) we have

$${{\rho }_{{\text{e}}}} = \frac{{\omega _{{\text{e}}}^{2}{{k}^{2}}}}{{4\pi }}\varphi \int {{{d}^{3}}{v}f({\mathbf{v}})g(\omega - {\mathbf{k}} \cdot {\mathbf{v}}).} $$

Here, f(v) is the distribution function normalized by the condition

$$\int {{{d}^{3}}{v}f({\mathbf{v}}) = 1.} $$

In the case of plasma consisting of particles of different kinds “a,” the perturbation of the total-charge density is

$$\rho = \frac{{{{k}^{2}}}}{{4\pi }}\varphi \sum\limits_{\text{a}}^{} {\omega _{{\text{a}}}^{2}{{J}_{{\text{a}}}},} $$

(19)

where

$${{J}_{{\text{a}}}} = \int {{{d}^{3}}{v}{{f}_{{\text{a}}}}({\mathbf{v}}){{g}_{{\text{a}}}}(\omega - {\mathbf{k}} \cdot {\mathbf{v}}),} $$

(20)

$${{g}_{{\text{a}}}}(\omega - {\mathbf{k}} \cdot {\mathbf{v}}) = \frac{{{{{\sin }}^{2}}\theta }}{{{{{(\omega - {\mathbf{k}} \cdot {\mathbf{v}})}}^{2}} - \omega _{{{\text{Ba}}}}^{2}}} + \frac{{{{{\cos }}^{2}}\theta }}{{{{{(\omega - {\mathbf{k}} \cdot {\mathbf{v}})}}^{2}}}},$$

$${{\omega }_{{{\text{Ba}}}}} = \frac{{{{q}_{{\text{a}}}}B}}{{{{m}_{{\text{a}}}}c}}.$$

According to the Landau rule, which follows from the causality principle, we have to make the substitution ω → ω + i0 in Eq. (20).

For ions, we can assume ω_Bi = 0 due to a large ion mass and write

$${{g}_{{\text{i}}}} = \frac{1}{{{{{(\omega - {\mathbf{k}} \cdot {\mathbf{v}})}}^{2}}}}.$$

Let plasma have a foreign charge with the density

$${{\rho }_{{{\text{ex}}}}} = {{\rho }_{0}}\exp (i{\mathbf{k}} \cdot {\mathbf{r}} - i\omega t).$$

(21)

apart from the inherent plasma charges. We rewrite Eq. (19) as

$$\rho = - {{k}^{2}}\chi \varphi ,$$

where

$$\chi = - \frac{1}{{4\pi }}\sum\limits_{\text{a}}^{} {\omega _{{\text{a}}}^{2}{{J}_{{\text{a}}}}} $$

is the plasma polarizability. Using Poisson’s equation

$$\nabla \cdot {\mathbf{E}} = 4\pi (\rho + {{\rho }_{{{\text{ex}}}}})$$

and Eq. (13), we find

$$\varphi = \frac{{4\pi }}{{\varepsilon {{k}^{2}}}}{{\rho }_{{{\text{ex}}}}},$$

(22)

where ε ≡ ε(k, ω) = 1 + 4πχ is the longitudinal plasma permittivity. In the case of an arbitrary foreign-charge density ρ_ex = ρ_ex(r, t), the electric potential induced by foreign changes in plasma is

$$\varphi ({\mathbf{r}},t) = \int {\frac{{{{d}^{3}}kd\omega }}{{{{{(2\pi )}}^{4}}}}\frac{{4\pi {{\rho }_{{{\text{ex}}}}}({\mathbf{k}},\omega )}}{{\varepsilon ({\mathbf{k}},\omega ){{k}^{2}}}}{{e}^{{i{\mathbf{k}} \cdot {\mathbf{r}} - i\omega t}}}.} $$

The relation φε particle size (k, ω) = 0 follows from Eq. (22) in the absence of foreign changes. In the presence of a wave, we have φ ≠ 0 and can write Eq. (3).

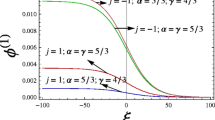
We now consider the distribution

$${{f}_{{\text{a}}}}({\mathbf{v}}) = \frac{{{{\Delta }_{{\text{a}}}}}}{{{{\pi }^{2}}{{{[{{{({\mathbf{v}} - {{{\mathbf{u}}}_{{\text{a}}}})}}^{2}} + \Delta _{{\text{a}}}^{2}]}}^{2}}}}.$$

We change the variable of integration V = v – u_a in Eq. (20) and obtain

$${{J}_{{\text{a}}}} = \frac{{{{\Delta }_{{\text{a}}}}}}{{{{\pi }^{2}}}}\int {{{d}^{3}}V\frac{{{{g}_{{\text{a}}}}(\omega + i0 - {\mathbf{k}} \cdot {{{\mathbf{u}}}_{{\text{a}}}} - {\mathbf{k}} \cdot {\mathbf{V}})}}{{{{{({{V}^{2}} + \Delta _{{\text{a}}}^{2})}}^{2}}}}.} $$

To calculate this integral, we direct axis z along vector k and perform integration over the velocity components that are perpendicular to this axes; as a result, we have

$${{J}_{{\text{a}}}} = \frac{{{{\Delta }_{{\text{a}}}}}}{{{{\pi }^{2}}}}\int\limits_{ - \infty }^\infty {d{{V}_{z}}\frac{{{{g}_{{\text{a}}}}(\omega + i0 - {\mathbf{k}} \cdot {{{\mathbf{u}}}_{{\text{a}}}} - k{{V}_{z}})}}{{V_{z}^{2} + \Delta _{{\text{a}}}^{2}}}.} $$

Three poles of the integrand lie in the upper half-plane of complex variable V_z and the fourth pole, V_z = –iΔ_a, lies in the lower half-plane. Closing the path of integration in the lower half-plane, we obtain

$$\begin{gathered} {{J}_{{\text{a}}}} = \frac{{{{{\sin }}^{2}}\theta }}{{{{{(\omega - {\mathbf{k}} \cdot {{{\mathbf{u}}}_{{\text{a}}}} + ik{{\Delta }_{{\text{a}}}})}}^{2}} - \omega _{{{\text{Ba}}}}^{2}}} \\ + \frac{{{{{\cos }}^{2}}\theta }}{{{{{(\omega - {\mathbf{k}} \cdot {{{\mathbf{u}}}_{{\text{a}}}} + ik{{\Delta }_{{\text{a}}}})}}^{2}}}}. \\ \end{gathered} $$

Finally, Eq. (3) takes the form of Eq. (6).