Lagrangian Stochastic Modelling of Dispersion in the Convective Boundary Layer with Skewed Turbulence Conditions and a Vertical Density Gradient: Formulation and Implementation in the FLEXPART Model

Abstract

A correction for the vertical gradient of air density has been incorporated into a skewed probability density function formulation for turbulence in the convective boundary layer. The related drift term for Lagrangian stochastic dispersion modelling has been derived based on the well-mixed condition. Furthermore, the formulation has been extended to include unsteady turbulence statistics and the related additional component of the drift term obtained. These formulations are an extension of the drift formulation reported by Luhar et al. (Atmos Environ 30:1407–1418, 1996) following the well-mixed condition proposed by Thomson (J Fluid Mech 180:529–556, 1987). Comprehensive tests were carried out to validate the formulations including consistency between forward and backward simulations and preservation of a well-mixed state with unsteady conditions. The stationary state CBL drift term with density correction was incorporated into the FLEXPART and FLEXPART-WRF Lagrangian models, and included the use of an ad hoc transition function that modulates the third moment of the vertical velocity based on stability parameters. Due to the current implementation of the FLEXPART models, only a steady-state horizontally homogeneous drift term could be included. To avoid numerical instability, in the presence of non-stationary and horizontally inhomogeneous conditions, a re-initialization procedure for particle velocity was used. The criteria for re-initialization and resulting errors were assessed for the case of non-stationary conditions by comparing a reference numerical solution in simplified unsteady conditions, obtained using the non-stationary drift term, and a solution based on the steady drift with re-initialization. Two examples of “real-world” numerical simulations were performed under different convective conditions to demonstrate the effect of the vertical gradient in density on the particle dispersion in the CBL.

1 Introduction

The need to use a density correction for Lagrangian stochastic (LS) particle modelling of dispersion in the atmospheric boundary layer was discussed by Thomson (1995) for the random displacement model and by Stohl and Thomson (1999) for stochastic models of the particle velocity. However, the general theory of Thomson (1987) included the possibility of a non-constant density flow. Stohl and Thomson (1999) pointed out that, in the case of a deep (of the order 2–3 km) convective boundary layer (CBL), the density of the air at the CBL top may be less than 80 % of its value at the ground level. If a density correction is not implemented in a LS model based on the well-mixed criterion proposed by Thomson (1987), the density variation may lead to significant underestimation of the concentration near the ground and corresponding overestimation of the concentration near the top of the boundary layer. Such errors in the vertical particle distribution can subsequently also result in horizontal transport errors due to vertical wind shear. In Stohl and Thomson (1999), this correction was actually formulated in terms of a Gaussian probability density function (PDF) for the vertical component of the velocity vector. However, it is accepted nowadays that a better model of the velocity PDF for a deep CBL is obtained using a skewed PDF that accounts for the strongly skewed nature of the turbulent fluctuations of the vertical velocity component. The CBL is characterized by updraft and downdraft structures, where fast ascent in relatively small updraft regions is compensated by slower descending motions in the rest of the CBL (e.g. Stull 1988). When modelling dispersion in the CBL by means of LS models, a formulation of the PDF that is based on the sum of two Gaussians distributions has been proven successful (e.g. Luhar and Britter 1989). One Gaussian distribution represents the updraft and the other represents the downdraft. Therefore, here we extend the work of Stohl and Thomson (1999) including a density correction in the model of Luhar et al. (1996), formulated using the well-mixed criterion and assuming a skewed PDF based on the sum of two Gaussians PDFs. Since backward-in-time modelling is extensively used in many applications (e.g. Flesch et al. 1995; Kljun et al. 2002; Seibert and Frank 2004), for completeness and clarity we discuss in some detail the backward-in-time formulation of this model based on Thomson (1987), and we perform consistency tests between backward and forward simulations. The formulation of Luhar et al. (1996) assumes that the turbulent statistics are horizontally homogeneous and stationary and, to our knowledge, many operational implementations of the Lagrangian stochastic model used nowadays neglect the horizontal and time derivatives of the turbulence statistics in the model formulation. A noticeable exception is the TAPM model described in Luhar and Hurley (2003) that uses an unsteady extension of the quadratic model of Franzese et al. (1999). However, the calculation of the trajectories may extend over time and space scales for which these assumptions are not perfectly valid. Here, to give some quantitative evaluation of what this inconsistency implies, the CBL drift formulation has been extended to include unsteady turbulence statistics, and tests have been carried out comparing results obtained using the steady and unsteady drift formulations under artificial analytical formulations of non-stationary turbulence conditions.

Finally, the steady skewed turbulence model is implemented in two versions of the operational LS model FLEXPART; the standard global scale model (e.g. Stohl et al. 2005) and a regional scale version FLEXPART-WRF (Brioude et al. 2013), the latter driven by the Weather Research and Forecasting model (e.g. Skamarock and Klemp 2008). The technical details of the implementation are given, and include a transition function that modulates the third moment of the vertical velocity based on stability parameters, and a re-initialization of the particle velocity similar to that of Wilson and Yee (2000). The re-initialization allows the use of the drift term formulated for steady and horizontally homogeneous conditions in non-stationary and horizontally inhomogeneous conditions. This was needed here since the numerical formulation of the steady and horizontally homogenous drift for the skewed PDF was found to be more sensitive than the standard Gaussian formulation to the time varying turbulence statistics and this, occasionally, introduced the possibility of a serious numerical degradation for the simulated particle trajectories. The bi-Gaussian drift formulation is intrinsically less stable than the Gaussian, as first noted by Luhar and Britter (1989) and discussed in Yee and Wilson (2007), and the instability phenomenon noted here is similar to the phenomenon of “rogue trajectories” discussed in detail in Yee and Wilson (2007) and Postma et al. (2012). However, here the main cause of instability appears to be the inconsistency between the formulation of the model (i.e. steady drift) and the time-varying turbulence statistics, and not the numerical implementation of the model itself, or the intrinsic dynamical instability of the stochastic differential equation since, with a sufficiently small timestep, no instability was observed in the case of the time-varying drift formulation.

2 Model Description

The discussion is limited to the one-dimensional case since the vertical component of velocity is here considered to be statistically independent of the horizontal components, and moreover horizontal homogeneity is assumed. The general form of the stochastic differential equations for the fluctuating particle vertical velocity is,

$$\begin{aligned} dw&= a (z,w,t)dt+b(z,t)dW, \end{aligned}$$

(1a)

$$\begin{aligned} dz&= wdt, \end{aligned}$$

(1b)

where $w$ is the fluctuating (turbulent) component of the particle vertical velocity, $z$ is the vertical coordinate, $a$ is the drift term, $b$ is the diffusion coefficient, and $dW$ is the increment of an independent Wiener process with zero mean and variance $dt$. If, following Thomson (1987), it is assumed that $f_a$, the density function of the distribution in phase space of air parcels, is known, and that the diffusion coefficient is already defined, then the drift coefficient can be obtained according to the well-mixed criterion as,

$$\begin{aligned} a=\frac{\varphi }{f_a }+\tilde{a}, \end{aligned}$$

(2)

where for a stationary vertically non-homogeneous flow,

$$\begin{aligned} \varphi =\varphi _z \equiv -\frac{\partial }{\partial z}\int \limits _{-\infty }^w {w'} f_a ({w}')d{w}', \end{aligned}$$

(3)

with the conditions that $\varphi \rightarrow 0$ when $\left| w \right| \rightarrow \infty$ and,

$$\begin{aligned} \tilde{a}=\frac{1}{f_a }\frac{\partial }{\partial w}\left( {\frac{1}{2}b^{2}f_a } \right) . \end{aligned}$$

(4)

We used $\varphi _z$ to emphasize that only the vertical non-homogeneity is considered in this formulation, and to distinguish it from a non-stationary term that is introduced below. The diffusion coefficient $(b)$ is usually defined (e.g. Wilson and Sawford 1996; Thomson and Wilson 2013) according to the Lagrangian structure function in the inertial subrange as $b=\left( {C_0 \varepsilon } \right) ^{1/2}$. Here $C_0$ should be the universal Kolmogorv’s constant for the Lagrangian structure function in the inertial subrange, and $\varepsilon$ is the mean dissipation rate of turbulent kinetic energy. However, in non-homogeneous and non-isotropic turbulence the value of $C_0$ seems not unique (e.g. Rodean 1996; Poggi et al. 2008) and in LS modelling its value is influenced by several factors (Thomson and Wilson 2013), and it could also be interpreted as a modelling constant (Pope 2000). It is appropriate to recall here that the relationship $T_L =2\sigma _w^2 /(C_0 \varepsilon )$ (Tennekes 1979) can be used to rewrite the equations in term of a local Lagrangian de-correlation time scale $T_\mathrm{L}$, which gives $b=\left( {2\sigma _w^2 /T_L } \right) ^{1/2}$. Although originally obtained for Gaussian homogenous turbulence this relation was used for the CBL by e.g. Luhar and Britter (1989), Luhar and Sawford (1995) and Franzese et al. (1999). For the specific case of the CBL, and following Baerentsen and Berkowicz (1984), Luhar and Britter (1989) and Luhar et al. (1996), the PDF for the vertical velocity statistics can be assumed to be defined as the sum of two Gaussian PDFs,

$$\begin{aligned} f_w =A g_{A}+B g_{B}, \end{aligned}$$

(5)

where $g_{A}$ and $g_{B}$ are the PDFs of the vertical velocity within the updraft and downdraft respectively, while $A$ and $B$ are related to the updraft and downdraft areas respectively, and represent the probability of occurrence of an updraft or downdraft in an ensemble-averaged sense,

$$\begin{aligned} g_{A}={\exp \left[ -(w-m_A )^{2}/(2\sigma _A^2 )\right] }\Big /{\sqrt{2\pi \sigma _A^2 }},\end{aligned}$$

(6a)

$$\begin{aligned} g_{B}={\exp \left[ -(w+m_B )^{2}/(2\sigma _B^2 )\right] }\Big /{\sqrt{2\pi \sigma _B^2 }}. \end{aligned}$$

(6b)

Here $m_A$ and $m_B$ are the magnitudes of the average velocity of the updraft and downdrafts while $\sigma _A$ and $\sigma _B$ are the respective standard deviations. However, as with Stohl and Thomson (1999) we introduce a vertically variable mean density $\rho (z)$ and therefore the density function of the distribution of the air parcels, $f_a$, appearing in Eq. 4, must be written as $f_a \propto \rho \,f_w$ and not just $f_a \propto f_w$, where the proportionality is used since the normalization is irrelevant in this context (Stohl and Thomson 1999). In case of a stationary and constant density flow, the explicit formulation of the term $\varphi$ (Eq. 3) for the PDF in Eq. 5 has been given by Luhar and Britter (1989) and in a slightly more general form by Luhar (1991) and Luhar et al. (1996). For the present case of a vertically variable density flow the distribution is given by

$$\begin{aligned} f_a (w,z)\propto \rho (z)A\,(z)g_{A}(w,z)+\rho (z)B\,(z)g_{B}(w,z), \end{aligned}$$

(6c)

and the drift formulation for constant mean density of Luhar et al. (1996) must be accordingly modified to,

$$\begin{aligned} \varphi _z&= -\frac{1}{2}\left( {A\rho \frac{\partial m_A }{\partial z}+\rho m_A \frac{\partial A}{\partial z}+Am_A \frac{\partial \rho }{\partial z}} \right) \hbox {erf}\left( {\frac{w-m_A }{\sqrt{2}\sigma _A }} \right) \nonumber \\&+\,\sigma _A g_{A}\left\{ {A\rho \frac{\partial \sigma _A }{\partial z}\left( {\frac{w^{2}}{\sigma _A^2 }+1} \right) +\frac{A\rho w}{\sigma _A^2 }\left( {\sigma _A \frac{\partial m_A }{\partial z}-m_A \frac{\partial \sigma _A }{\partial z}} \right) +\sigma _A \left( {\rho \frac{\partial A}{\partial z}+A\frac{\partial \rho }{\partial z}} \right) } \right\} \nonumber \\&+\,\frac{1}{2}\left( {B\rho \frac{\partial m_B }{\partial z}+\rho m_B \frac{\partial B}{\partial z}+Bm_B \frac{\partial \rho }{\partial z}} \right) \hbox {erf}\left( {\frac{w+m_B }{\sqrt{2}\sigma _B }} \right) \nonumber \\&+\,\sigma _B g_{B}\left\{ {B\rho \frac{\partial \sigma _B }{\partial z}\left( {\frac{w^{2}}{\sigma _B^2 }+1} \right) +\frac{B\rho w}{\sigma _B^2 }\left( {m_B \frac{\partial \sigma _B }{\partial z}-\sigma _B \frac{\partial m_B }{\partial z}} \right) +\sigma _B \left( {\rho \frac{\partial B}{\partial z}+B\frac{\partial \rho }{\partial z}} \right) } \right\} ,\nonumber \\ \end{aligned}$$

(7)

where new terms arise as a result of the vertical variation of the air density. This is an extension of Luhar et al. (1996) following Thomson (1987). To our knowledge Eq. 7 has not been previously reported in the literature.

The complete formulation of $\tilde{a}$ is,

$$\begin{aligned} \tilde{a}=-\frac{C_0 \varepsilon }{2f_a }Q, \end{aligned}$$

(8)

with,

$$\begin{aligned} Q=\frac{A\rho (w-m_A )}{\sigma _A^2 }g_{A}+\frac{B\rho (w+m_B )}{\sigma _B^2 }g_{B}. \end{aligned}$$

(9)

2.1 Backward-in-Time Formulation

For clarity and completeness, we report the backward formulation of the above forward model, which is used frequently in practical applications of LS dispersion models (e.g. Seibert and Frank 2004). Following Thomson (1987) a system of coordinates ${t}'=-t$ and ${w}'=-w$ is set where the reversed time ${t}'$ increases while we go backward in the true time relative to our initial time (set here to be zero). The differential equations defining the trajectory of a particle while going forward in reversed time (backward in real time) are therefore (Thomson 1987),

$$\begin{aligned} d{w}'&= {a}' (z,\,w,\,t)d{t}'+b(z,\,t)dW,\end{aligned}$$

(10a)

$$\begin{aligned} dz&= {w}'d{t}', \end{aligned}$$

(10b)

with the drift coefficient defined as

$$\begin{aligned} {a}'=\frac{\varphi }{f_a }-\tilde{a}=\frac{\varphi }{f_a }+\frac{C_0 \varepsilon }{2f_a }Q, \end{aligned}$$

(11)

with $\varphi ,\, f_a ,\, Q$ and $\varepsilon$ evaluated at $(z=z,\,w=-{w}',\,t=-{t}')$.

2.2 Relationship Between $g_{A}$, $g_{B}$ and the Vertical Velocity Statistics

As can be seen in Eqs. 5, 6, 7 and 9 the actual value of the drift coefficient depends on the values assumed for the variables defining the updraft and downdraft velocity distributions i.e. $A,\,B,\,m_A ,\,m_B ,\,\sigma _A ,\,\sigma _B$. Relating these variables to the first four moments (0–3) of the vertical velocity distribution results in an unclosed system of four equations and six unknowns and various closures have been proposed to obtain a closed system. A review is given in Luhar et al. (1996), and here the closure method originally proposed by them is used. This closure has the remarkable property of allowing the sum of the two Gaussian PDFs in (5) to become a Gaussian distribution in the limit of the skewness going to zero. This closure is defined as $m_A =(2/3)S^{1/3}\sigma _A ,\,m_B = (2/3)S^{1/3}\,\sigma _B$ where $S$ is the skewness. The resulting definitions for the updraft and downdraft variables are reported in Appendix 1 for completeness while details can be found in Luhar et al. (1996, 2000).

In the present work various definitions for the second moment of the fluctuating vertical velocity are used and references are given when appropriate, but we use in general the following parametrization of the third moment, originally proposed by Luhar et al. (2000),

$$\begin{aligned} \left\langle {w^{3}} \right\rangle =w_{*}^3 \left( {1.2\,(z/h)(1-z/h)^{3 / 2}} \right) , \end{aligned}$$

(12)

where $w_{*}$ is the convective scaling velocity (see e.g. Stull 1988) and $h$ is the depth of the CBL.

3 Validation

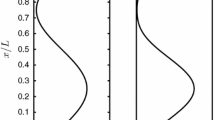
Following Stohl and Thomson (1999) the formulations in (6), (7) and (8) were firstly validated using an imposed artificial exponential decrease of the air density with elevation, $\rho =\exp (-z/h)$. As explained in Stohl and Thomson (1999) this is a sharper density gradient than typically occurs in the real atmosphere and therefore should reveal the model capability. According to Luhar et al. (2000) the second moment of the vertical velocity is defined as $\left\langle {w^{2}} \right\rangle =w_{*}^2 \left( {1.7\,(z /h\,(1-0.7z/h)\,(1-z/h))^{2/3}} \right)$, a value of $C_0 =3$ was used, and perfect reflection conditions were imposed at the computational boundaries set to be at a distance of $4\times 10^{-5}h$ from the physical boundaries. The variable integration timestep was set to $\Delta t=0.005T_L$ . This timestep is rather short but we found it was needed, using the simple Euler-Maruyama discretization scheme (e.g. Kloeden et al. 1994), to have an accurate solution. In addition, this short timestep seems, for the cases investigated here, to avoid the numerical issues that may arise due to the intrinsic dynamic instability and the stiffness of the Langevin model used (see Yee and Wilson 2007). The particles were initially randomly distributed in the vertical domain following the imposed vertical air density distribution and extracting the particle velocity from the sum of the two Gaussian PDFs (Eq. 5). This results in an initial particle distribution that, apart from numerical approximations and statistical noise, should be maintained by the model if the formulation respects the well-mixed condition (i.e. particles that are initially well-mixed will remain so). This is confirmed in Fig. 1 for a forward (upper panels) and backward (lower panels) simulation; the normalized particle density is shown as a shaded contour, as a function of dimensionless height $(z/h)$ and dimensionless time, $T=tw_{*} /h\, (T={t}'w_{*} /h$ for the backward simulation), and as vertical profiles for the dimensionless height in the initial and final time of the simulations (Fig. 1b, d). It is worth remarking that in the case of the backward simulation the particle velocity initialization is different since the velocity is ${w}'=-w$, i.e. after randomly extracting a value from the PDF, Eq. 5, the sign of the velocity is reversed. This is exemplified in Fig. 2 that shows the particle density resulting from a localized instantaneous source in a forward simulation (a, c) and backward simulation (b, d) for two different initial source elevations. It can be seen in the case of the backward simulations that the particles have a different initial velocity with higher probability of weak positive vertical velocity. To confirm that the model is performing properly the following general relation between forward and backward transition probability densities (see Thomson 1987),

$$\begin{aligned} f(z_1 ,t\left| {z_0 ,s)\rho (z_0 ,s)} \right. =f(z_0 ,s\left| {z_1 ,t)\rho (z_1 ,t)}, \right. \end{aligned}$$

(13)

needs to be fulfilled, where $t>s$ and $f(z_1 ,t\left| {z_0 ,s)} \right.$ is the probability density that a particle passing $z_0$ at the time $s$ will be in $z_1$ at the time $t$. These probability densities are calculated by releasing particles in a point $z_0 \,[z_1 ]$ and moving the particles forward [backward] in time for $f(z_1 ,t\left| z_0 ,s)\,\right. \, [f(z_0 ,s\left| {z_1 ,t)} \right. ]$. The particles must afterwards be sampled in a small discrete interval around the arrival point $z_1 \,[z_0]$. Since our driving velocity and density are stationary, as a test we could just consider the previously shown forward simulation in Fig. 2c and sample its output along the arrival point $z_1 =0.49$ for any value of $t$ and compare the result with the backward simulation in Fig. 2b sampling the output at $z_0 =0.01$ for any value of $-t$. Multiplying by the starting point air densities as required by (13) this is plotted in Fig. 3 and the consistency of the forward and backward formulation seems to be confirmed.

Fig. 1

Normalized particle density as a function of dimensionless height and time from the release for a forward-in-time simulation (upper panels) and a backward-in-time simulation (lower panels). a, c The evolution in time starting from the initial imposed well-mixed state. b, d The initial state ($T=0$, circles) and the final state ($T=6$ crosses). In b and d the continuous line shows the imposed normalized density of the air

Fig. 2

Normalized particle density for sources of vertical extension $h/50$ centered at $0.49h$ (a, b) and located at the ground level (c, d) as a function of dimensionless height and time from release, for forward-in-time (a, c) and backward-in-time (b, d) simulations

Fig. 3

Forward (abscissa) transition probability density resulting from a source of vertical extension $\Delta z/h=1/50$ placed at the ground and a sampling bin of the same size centered at $0.49h$ for various times after release $(t)$, versus the backward (ordinate) transition probability density resulting from a source of size $\Delta z/h=1/50$ centered at $0.49h$ with a sampling bin of the same size at ground level, and for corresponding inverse time intervals $(-t)$. The two densities are multiplied by the air density as required by Eq. 13

4 Implementation in FLEXPART

The CBL-skewed turbulence model described above has been implemented in the FLEXPART model, both in the global-scale model (e.g. Stohl et al. 2005), and in the regional-scale version FLEXPART-WRF recently introduced by Brioude et al. (2013). This implementation is not totally straightforward since currently the FLEXPART model, as with many other LS particle models, neglects the horizontal and time derivatives of the turbulence properties in the model formulation and considers the calculation of the trajectories in a stationary state. In reality, however, the calculations typically extend over time and space scales for which the assumptions of stationarity and horizontal homogeneity are not perfectly valid. Changes of the parametrized turbulent field in the model occur due to the change of the stability and/or the mixing height that a particle encounters as it moves in space and time. Moreover, with the skewed PDF formulation and depending on the parametrizations for the second and third moments of the vertical velocity, there is the possibility of a non-continuous transition between a skewed and a non-skewed PDF if (in the model) the transition between neutral and unstable conditions is not set to happen at $w_{*} =0$ (i.e. $h/L=0$, where $L$ is the Obukhov length; see also Appendix 2 ). Therefore, two strategies are discussed and tested below that allow the use of the stationary skewed turbulence drift formulation in the FLEXPART model. First, an ad hoc transition function has been introduced (Sect. 4.1) to allow the continuous smooth transition of the PDF between a skewed and non-skewed formulation (and vice versa) depending on the stability conditions through the ratio $h/L$. Second, a particle velocity re initialization procedure has been introduced (Sect. 4.2.1) to avoid the possible occurrence of an unbounded particle velocity due to the inconsistent usage of a steady skewed drift formulation under unsteady conditions.

4.1 Transition Function from Near-Neutral to Unstable Conditions

First, we note that currently the FLEXPART model assumes neutral conditions for $\big | {h/L} \big |<1$. Second, we note that the dimensionless parametrization of the third moment of the fluctuating velocity in Eq. 12 is based on mixed-layer scaling arguments that apply (see e.g. Luhar and Britter 1989; Holtslag and Nieuwstadt 1986; Rodean 1996) when $-h/L>10$. Holtslag and Nieuwstadt (1986) proposed a stability diagram where, for $1<-h/L<10$, the conditions are near neutral up to the top of the boundary layer, while for $-h/L>10$ the convective scaling applies for a progressively growing portion of the boundary layer (see also Rodean 1996). Furthermore, the observations of the third moment of velocity available in the literature (see e.g. Franzese et al. 1999 and the Fig. 4) are quite scattered. Based on these premises a transition function is proposed here that allows the third moment of the vertical velocity to continuously change between zero, in near-neutral conditions (defined here as $1<-h/L\le 5)$, to its maximum value, given by Eq. 12, in strongly unstable conditions (defined here as $-h/L\ge 15)$. This means that, using the properties of the closure proposed by Luhar et al. (1996) to define the velocity PDF, the vertical velocity PDF changes continuously from the Gaussian for $-h/L\le 5$ to a skewed PDF. The transition function is defined as,

$$\begin{aligned} \alpha (h/L)=\left\{ {\begin{array}{l} 0\,{\hbox {for}}-h/L\le 5 \\ \hbox {sin}\left( {\frac{-h/L+10}{10}\pi } \right) /2+\frac{1}{2}\quad {\hbox {for}}\;\,5<-h/L<15 \\ 1\,{\hbox {for}}-h/L\ge 15 \\ \end{array}}. \right. \end{aligned}$$

(14)

Therefore, the third moment effectively used in the FLEXPART model is

$$\begin{aligned} \left\langle {w^3} \right\rangle =\alpha \,{w_{*}^{3}} \left( {1.2\,(z/h)(1-z/h)^{3/2}} \right) . \end{aligned}$$

(15)

Fig. 4

Vertical profile of the dimensionless third moment of the turbulent vertical velocity resulting from Eq. 15, and various experimental measurements as reported in Franzese et al. (1999): (triangle) Lenschow et al. (1980; circle) Luhar et al. (1996; diamond) Willis, from Baerentsen and Berkowicz (1984)

The third moment resulting from this parametrization agrees with the range of measurements as collected by Franzese et al. (1999) and shown here in Fig. 4, for $-h/L\ge 10$ (at $-h/L=10$ the third moment is within the range of the measurements). A point that needs to be underlined is that, by using the transition function, we do not want to imply that in the actual atmosphere there is an observed dependence of the dimensionless (scaled by $w_*$) third moment on $-h/L$; the transition function is a modelling expedient, and it is designed in this way since without it the skewness of the vertical velocity would be zero only when $w_*$ is exactly zero. This, in turn, as discussed in more detail in Appendix 2, means that with the parametrizations used in FLEXPART and without the transition function, a continuous PDF change can be assured only when switching to the skewed PDF formulation at $-h/L=0$. For any other threshold value for the switch (e.g. $-h/L=1$ or $-h/L=10$), a discontinuous PDF would be created. However, as discussed above, even for $-h/L>1$, the stability conditions may be considered near-neutral and therefore a Gaussian PDF seems appropriate to describe the dispersion process. In this respect, we mention that the use of a bi-Gaussian skewed PDF is very appropriate to describe the dispersion under the skewed turbulence conditions of the CBL but there seems to be no support for the use of this skewed PDF in other skewed turbulence conditions. For example, Flesch and Wilson (1992) discuss the poor performance, when compared to a Gaussian PDF, of a bi-Gaussian PDF (including the correlation between $u$ and $w$) under the skewed turbulence conditions of flow through and above a canopy. In general, other skewed PDFs are possible (e.g. Thomson 1987; Cassiani et al. 2005) and may be used under non-convective skewed turbulence conditions, but with no complete understanding, the Gaussian velocity PDF seems to be a “safe” and computationally very efficient choice, which gives an adequate description of dispersion in most conditions other than the fully convective case. For this reason using (14) we allowed that the drift formulation in the operational FLEXPART models becomes the simpler Gaussian PDF as reported in Stohl and Thomson (1999, Eq. 3) whenever $-h/L\le 5$. Since, as shown in Fig. 4, for $-h/L=10$ the third moment is already within the range of measurements, and rapidly growing to its maximum value for $-h/L\ge 15$, we believe that our choice for the transition function is sensible, with some arbitrariness only for the range $5<-h/L<10$.

It is worth reminding the reader that a different approach is possible (Rotach et al. 1996; Tassone et al. 1994) where the PDF itself is composed of a weighted sum of a skewed PDF and a Gaussian PDF. The weight is based on a transition function of stability while the third moment is not modified, i.e. the functional change in the PDF does not depend directly on the value of the velocity moments. We also note that, in their approach, Rotach et al. (1996) included in the drift formulation the correlation between the alongwind and vertical velocity fluctuations in neutral conditions, which is instead neglected here and in FLEXPART. This correlation may have some impact on the dispersion (see e.g. the analysis of Wilson et al. 1993). More generally, for neutral stability in complex three-dimensional conditions, like those of a flow in complex terrain or through urban obstacles, one could include the full off-diagonal components of the stress tensor in the drift formulation of the Thomson (1987) model, as discussed for example in Näslund et al. (1994), Yee and Wilson (2007) and Weil (2008). However, when the coordinate system is aligned with the local mean wind direction (as in FLEXPART) Näslund et al. (1994) report, for a very complex three-dimensional flow past an obstacle, “a rather weak dependence of the Langevin equation model (dispersion results) on the off-diagonal stresses” (see also Yee and Wilson 2007).

4.2 Tests of the Approximations Involved in Using a Stationary Drift Term with a Non-stationary Condition

The transition function smooth the effects of a change in the stability conditions. However, we are still using a stationary and horizontally homogeneous formulation under non-stationary and horizontally non-homogeneous conditions. To test the level of approximation involved in using the stationary formulation in a non-stationary flow we extend the formulation of the drift coefficient in Eq. 7 to include unsteadiness of the turbulent parametrization, i.e. we extend the Eulerian PDF to the general form,

$$\begin{aligned} f_a (w,z,t)\propto \rho (z)A(z,t)g_{A}(w,z,t)+\rho (z)B (z,t)g_{B}\,(w,z,t), \end{aligned}$$

which implies that the drift coefficient in Eqs. 2 and 3 has an additional term,

$$\begin{aligned} \varphi =\varphi _z +\varphi _t , \end{aligned}$$

(16)

with,

$$\begin{aligned} \varphi _t =-\frac{\partial }{\partial t}\int \limits _{-\infty }^w {f_a } ({w}')d{w}'. \end{aligned}$$

(17)

After the integration this term can be shown to be,

$$\begin{aligned} \varphi _t&= -\frac{1}{2}\left( {\rho \frac{\partial A}{\partial t}} \right) \left[ {\hbox {erf}\left( {\frac{w-m_A }{\sqrt{2}\sigma _A }} \right) +1} \right] -\rho Ag_{A}\left( {-\frac{w-m_A }{\sigma _A }\frac{\partial \sigma _A }{\partial t}-\frac{\partial m_A }{\partial t}} \right) \nonumber \\&-\frac{1}{2}\left( {\rho \frac{\partial B}{\partial t}} \right) \left[ {\hbox {erf}\left( {\frac{w+m_B }{\sqrt{2}\sigma _B }} \right) +1} \right] -\rho Bg_{B}\left( {-\frac{w+m_B }{\sigma _B }\frac{\partial \sigma _B }{\partial t}+\frac{\partial m_B }{\partial t}} \right) . \end{aligned}$$

(18)

Although this is a straightforward application of the original work of Thomson (1987) this non-stationary drift coefficient for the bi-Gaussian PDF was not, to our knowledge, introduced before in the literature. Note that in this general formulation the parametrization of the turbulent flow at a specific elevation is allowed to change in time, for example due to a change in stability. The time derivative of the mean air density is not included in this 1D formulation since the mean continuity equation for the mean density (obtained from the Fokker-Planck equation) implies that it is zero if $\left\langle w \right\rangle =0$,

$$\begin{aligned} \frac{\partial \rho }{\partial t}=-\left\langle w \right\rangle \frac{\partial \rho }{\partial z}-\rho \frac{\partial \left\langle w \right\rangle }{\partial z}=0. \end{aligned}$$

(19)

More generally, the change in time of the air density can be included consistently if the spatial derivative of the mean velocity and density are included as well in the formulation.

In the following a comparison between the well-mixed particle state of the model including the non-stationary term (16) and the model using only the stationary drift (7) is performed with non-stationary parametrizations used to drive both models. These are tests of the mathematical and numerical formulations of the model and not meant to represent the typical meteorological conditions.

As a first test an artificial change in the stability is assumed as a change in the Obukhov length but with $h$ (set to 2,000 m) and $w_{*}$ (set to $1\,\hbox {m~s}^{-1}$) kept constant. The Obukhov length is varied following a linear decrease, $L=L_0 -C_l t$, with $C_l =1\,\hbox {m s}^{-1}$ and $L_0 =-20\,\hbox {m}$, and kept constant once $-h/L<5$. Based on the third moment in Eq. 15 and the second moment as in Luhar et al. (2000) this test implies a transition from the fully skewed PDF to the Gaussian PDF after 380 s. of the simulated time. To better appreciate the perturbation from the well-mixed state, the normalized error $(E)$ as a function of elevation is defined as,

$$\begin{aligned} E(z_i)=\frac{\rho ^{{*}}(z_i )-\exp (-z_i /h)}{\exp (-z_i /h)}, \end{aligned}$$

(20)

where $\exp (-z/h)$ is the assumed air density profile and the density obtained from the particles, $\rho ^{{*}}$, is computed as,

$$\begin{aligned} \rho ^{{*}}(z_i )=\left( {\frac{n_i^p }{N_h^p }} \right) \left( {\frac{N_z }{h}} \right) \int \limits _0^h {\exp (-z/h)dz} . \end{aligned}$$

(21)

Here $z_i$ is the elevation of the centre of a sampling bin of width $h/N_z$ with $N_z$ (set to 25) being the constant total number of vertical bins in the planetray boundary layer (PBL); $n_i^p$ is the number of particles in the i-th bin and $N_h^p$ is the total number of particle within the PBL.

Figure 5 shows the results of this comparison with panel (a) reporting the results of the non-stationary drift, and panel (b) the results with the stationary drift. The two panels use exactly the same intervals. Clearly the non-stationary drift maintains very well the initial uniform distribution of particles, with fluctuations always smaller than 5 % (due to statistical noise), and no systematic numerical bias observable at this resolution, which also serves to validate Eq. 18. The stationary drift as expected does not perform as well due to its intrinsic limitations. A systematic error with absolute maxima between 5 and 10 % arises. This systematic error tends to disappear later on in the simulation, since after 380 s the Obukhov length $L$ is kept constant and a constant neutral stratification is maintained. The error peaks after the transition to the neutral state is complete and this is likely due to the fact that the initial particle positions are well-mixed, so the velocity is firstly altered by the inaccurate drift term before the position being also significantly altered. Therefore, after 380 s the positions are still nearly well-mixed with respect to position but their velocities are significantly away from the correct velocity PDF (i.e. the distribution in the velocity space is not at the well-mixed state) and this generates the subsequent visible deviation of the particles from the well-mixed state in the physical space. However, with the use of the transition function in Eq. 14 and the current setting of the relevant scaling parameters the systematic error is bounded to a maximum value between 5 and 10 %, which may be acceptable for most applications.

Fig. 5

Normalized error ($E$, see text) from the assumed initially well-mixed distribution of particles, $\rho =\exp (-z/h)$, given a non-stationary parametrization by varying Obukhov length $(L)$ and using the non-stationary drift formulation (a) and the stationary drift formulation (b)

As a second test the boundary-layer height is reduced linearly according to $h=h_0 -C_h t$, with $C_h =1\,\hbox {km h}^{-1}$ and $h_0 =2\,\hbox {km}$, but keeping the scaled modelled third-moment profile constant with $L=L_0$ and therefore, $-h/L<15$. The convective velocity scale was set to 1 m s$^{-1}$, and the density profile is kept constant to $\rho =\exp (-z/h_0 )$. This means that, while the top of the boundary layer collapses, the particles remaining inside the boundary layer at a given elevation, $z$, experience a non-stationary turbulence parametrization (since $z/h$ changes) but with a constant vertical density profile. We used this decreasing mixing-layer test, instead of the more common situation of an increasing mixing-layer depth, because we believe it offers a more stringent test of the model capability. This is so because, during the growth, new particles must be introduced (in a perfectly well-mixed state) in the growing mixing layer domain at each timestep (corresponding to the free tropospheric air entrained). These particles are, by initialization, in a perfectly well-mixed state in phase space so that the perturbation to the well-mixed state by the use of a steady drift in unsteady conditions is reduced. Consequently, the case of a decreasing mixing-layer height provides a more stringent test on the performance of our scheme, even though it may not occur as often in nature.

Before discussing the results in detail it is necessary to clarify some aspects of the particle reflection scheme used at the top of the boundary layer. The reflection scheme used in this test is the same used in FLEXPART and implies that those particles that start an increment in their position below the top of the PBL are reflected inside the boundary layer if crossing the boundary (perfect reflection). However, when the PBL height decreases, the particles ending above the top of the PBL due to this decrease will remain outside the PBL. Note that in the numerical formulation the PBL depth is updated before any other variable is calculated. This implies also that while the PBL depth decreases fewer and fewer particles remain inside the PBL.

Figure 6 shows the calculated density profile using the non-stationary drift formulation during the collapse of the boundary layer from its initial state. The density obtained from the particles $(\rho ^{{*}})$ is computed here as,

$$\begin{aligned} \rho ^{{*}}(z_i )=\left( {\frac{n_i^p }{N_h^p }} \right) \left( {\frac{N_z }{h}} \right) \int \limits _0^h {\exp (-z/h_0 )dz}. \end{aligned}$$

(22)

It should be noted that the only difference from Eq. 21 is in the scaling constant, which is calculated using $\exp (-z/h_0 )$ since the density profile is considered stationary and does not change with the CBL depth. The upper line in the figure shows the top of the collapsing CBL, since the scaling variable for the vertical coordinate is the initial CBL depth $h_0$. In any case it seems that the initial density profile is well maintained, i.e. the well-mixed condition is respected as expected.

Fig. 6

Well-mixed normalized particle density $\rho ^{{*}}$ (shading) as computed by the model with the non-stationary drift formulation plotted as a function of scaled elevation and time. The thick solid line shows the assigned linear decrease of the CBL depth

To better appreciate any deviation from the well-mixed state the normalized errors $(E)$ from the air density well-mixed states are shown in Fig. 7; Fig. 7a presents the normalized error for the non-stationary drift formulation. It should be noted that in Fig. 7 the vertical coordinate is scaled by the evolving CBL depth. As expected the non-stationary drift formulation in Fig. 7a correctly maintains a vertically well-mixed state of the particles with $E < 5~\%$. This confirms again that the non-stationary drift term formulated in Eq. 18 is correct.

However, in this varying CBL depth test, it was found that the straightforward use of a stationary drift in unsteady conditions caused the simulation to break down due to the occurrence of an unbounded velocity. Therefore, a method was devised and tested to prevent this and is discussed below.

4.2.1 Velocity Re-initialization Procedure

Firstly a criterion for detecting particles potentially encountering numerical instability, before the particle position is strongly compromised by the excessive velocity, is defined as,

$$\begin{aligned} (\left| {w-m_A } \right| >C\,\sigma _A \,{\hbox {and}}\,\left| {w+m_B } \right| >C\,\sigma _B), \end{aligned}$$

and with $C=6$, although not impossible, this is a very unlikely event if the particle velocity is in equilibrium with the local turbulent conditions. Thus, its occurrence could be used as symptomatic of a numerically diverging solution for the particle trajectory in velocity space. For the present simulation, using a timestep of $0.005T_{L}$, the number of occurrences of the criterion above was about 1.5 % of the particle total number during a simulation lasting 1 h (about $2h/w_*$ based on an average boundary-layer depth). Secondly, to ensure continuity of the particle trajectories in physical space and to avoid numerical instability, a simple re-initialization procedure for the particle velocity was introduced and associated with the criterion above. In detail when the condition reported above is met by a particle along its trajectory this particle is re-initialized, randomly extracting a new value of velocity depending on the current location of the particle, and conditionally extracting a negative (positive) velocity from the downdraft (updraft) Gaussian velocity distribution if the discarded velocity was negative (positive). This procedure should ensure that the new velocities are on average correlated with the previous state and that the new velocity is in an acceptable equilibrium with the local turbulence conditions. Wilson and Yee (2000) used a similar but slightly more sophisticated criterion to detect unstable particle trajectories in their 3-D Gaussian stochastic model of dispersion in a modelled canopy. They also re-initialized the particle trajectories after detecting the instability, but discarding any correlation with the previous particle velocity.

Fig. 7

Relative error $(E)$ from the assumed density profile (i.e. from the well-mixed state) of an initially well-mixed distribution of particles given a non-stationary parametrization by varying CBL height $(h)$ and using the non-stationary drift formulation (a), and the stationary drift formulation (b, c) with different level of re-initialization for handling numerically diverging particle velocities (see text for details). It should be noted here that the vertical coordinate is scaled by the evolving CBL height

The results for the same experiment discussed above with varying CBL depth but using the stationary state drift by re-initializing the velocity are shown in Fig. 7b. Note that, close to the upper boundary, the deviation of the simulation from the correct well-mixed state can be between 5 and 10 %. This deviation has a similar magnitude to that observed in Fig. 5 for the non-stationary stability conditions with constant $h$ but it is of opposite sign close to the top of the boundary layer.

In reality the use of a steady drift in unsteady situations alters (albeit in a less evident manner) all the particle trajectories, and not only those encountering the condition above. To better understand the effect of re-initializing the particle trajectory two further tests have been conducted. First, the condition above was modified using $C=3$. In this way the particle re-initialization becomes much more frequent and also tends to occur earlier in the simulations. The results in Fig. 7c show that this more “invasive” particle re-initialization actually does not significantly change the deviation of the solution from the correct well-mixed state. As a second test of the effect of the re-initialization procedure the particle dispersion experiment reported in Fig. 2c, d (stationary state parametrization and drift) was repeated but randomly re-initializing the particle velocities at a rate of 100 % of the emitted particle number per dimensionless time interval $(T)$. In other words if $N$ particles are initially released these are afterward continuously and randomly sampled every timestep with a sampling rate that ensures that, after one dimensionless time interval, $N$ re-initializations are performed. The results of this simulation are shown in Fig. 8 and demonstrate that with this, quite high, rate of re-initialization a limited influence on the results is visible when compared to the unperturbed solution reported in Fig. 2c, d.

Therefore, we can state that: the re-initialization itself perturbs the results to a limited extent. For the cases investigated here this avoids the occurrence of numerical instability when using a stationary drift coupled with a non-stationary turbulence parametrization, as done for example in FLEXPART (thus allowing use of a steady drift in unsteady conditions), and it ensures continuous physical trajectories. On the other hand, some deviation from the perfect well-mixed state in physical space is present when using a stationary drift in non-stationary conditions and the re-initialization breaks the continuity of trajectories in velocity space.

Fig. 8

Normalized particle density for a source of vertical extension $h/50$ located at the ground as a function of dimensionless height and time from release using a re-initialization rate of 100 % of the particles per unit time interval. Forward-in-time (a), and backward-in-time (b)

5 Some Results in “Real World” Convective Conditions

A few example simulations are described here using FLEXPART (Stohl et al. 2005) and FLEXPART-WRF (Brioude et al. 2013), with the newly added steady drift formulation for the CBL, to illustrate the influence of the variable density for point source releases in a CBL under two quite different real-world convective conditions. The third moment of the velocity is parametrized as reported above in Eq. 15 while the second moment is derived from the standard parametrization used in FLEXPART based on Hanna (1982) (see Appendix 2 and the FLEXPART user manual for further details: http://transport.nilu.no/flexpart and http://flexpart.eu). It is worth noting that, when applied inside FLEXPART, the model is coupled with additional equations for the turbulent dispersion in the along-wind and crosswind directions and that the mean wind shear is taken into account.

First, to test the effects of the variable density correction an instantaneous (15 s) localized release in the Sahara desert at latitude of $18.45^{\circ }\hbox {N}$ and a longitude of $6.035^{\circ }\hbox {E}$ is simulated for 3 h (1200–1500 UTC) on 1 July 2011, forcing the model with ECMWF meteorological data . The position and release date were chosen for a very deep CBL, and for the particular case simulated here the CBL has a calculated depth of about 4.5 km with minimal variations in time and space during the simulation. The Obukhov length is calculated to be about $-5~\hbox {m}$, thus ensuring that the transition function, Eq. 14, has unit value. The convective velocity scale is about 3 $\hbox {m~s}^{-1}$ with minimal variations. Due to the rather coarse horizontal ($1^{\circ }$) and time (3 h) resolution of the meteorological data the conditions for the re-initialization did not occur (i.e. there was no use of the re-initialization procedure).

Six simulations were performed; three for constant density and three with the profile as obtained from the meteorological fields. For each density condition, ground level, mid-CBL, and top-of-the-CBL releases were simulated. In Fig. 9 the results are presented as horizontally-integrated and normalized concentration contours, as a function of time (in hours) and dimensionless elevation above ground. The effects of the variable density stratification are clearly visible both near the ground and near the top of the boundary layer with absolute values of the relative bias up to about 21 % of the simulated concentrations between constant density and variable density simulations. Far from the source the stratification due to a variable density is especially evident in the right panels. For similar simulations (not reported here) of a 3,200-m deep CBL, the absolute value of the relative bias was up to about 15 %.

Fig. 9

Time evolution of normalized horizontally-integrated concentration obtained from FLEXPART simulations of instantaneous releases of particles in a very deep CBL (4.5 km) assuming constant density profile (left panels) and using the actual vertically variable density. Simulations are for an instantaneous localized ground-level source (upper panels), a source in the middle of the CBL (middle panels) and a source near the top of the CBL (lower panels)

As a second example the FLEXPART-WRF model was run from 1500 to 1800 UTC on 29 June 2007, for an instantaneous (15 s) release located at $60.075^{\circ }\hbox {N},\,11.2^{\circ }\hbox {E}$. The meteorological conditions are convective but the CBL is not as deep as in the previous case. Also, the meteorological conditions varied more significantly in space and time. The stability parameters $(h,\,L,\,w_{*})$ are reported in Fig. 10 as averaged values over the ensemble of particle positions and as a function of time.

Fig. 10

Particle ensemble-averaged PBL parameters in the FLEXPART-WRF simulation as a function of time

The resulting horizontally-integrated and normalized concentration is reported in Fig. 11 with contour lines as a function of time and dimensionless elevation for both the constant density (left panel) and the variable density (right panel). In this simulation, the horizontal (10 km) and time (3 h) resolution of the meteorological fields required that only up to a maximum of 0.0001 % particles every 1,200 s needed to be re-initialized. Some differences between the two cases can be observed but, as expected given the lower elevation of the CBL top, they are more limited compared with the previous simulation for the very deep CBL, with absolute values of the relative bias up to a maximum of about 10 %, thus showing that the density correction is not as relevant for a moderately deep CBL. Stohl and Thomson (1999) calculated the relative bias in the ground-level concentration due to the density gradient in several experiments, with the ensemble-averaged PBL height ranging from 1,400 to 1,700 m. They obtained a relative bias up to 8 % and an averaged (including all experiments) value of 5.5 %. However, this average included one experiment where the PBL height at the release was as low as 400 m.

Fig. 11

As in Fig. 8 but for a FLEXPART-WRF simulation of a ground-level source in a moderately deep CBL (see Fig. 10)

6 Conclusions

Following Stohl and Thomson (1999) a density correction has been incorporated into the skewed PDF formulation for CBL turbulence proposed by Luhar et al. (1996), and the related drift term for a Lagrangian stochastic dispersion model has been obtained based on Thomson (1987) well-mixed condition. Furthermore, the formulation has been extended to include unsteady turbulent conditions and the related additional component of the drift term has been derived as well. To our knowledge these drift formulations were not previously presented in the literature. Tests were carried out to validate the formulations, including consistency between forward and backward simulations and the compliance with the well-mixed state in unsteady conditions.

The stationary state CBL drift term with density correction has been incorporated into the FLEXPART and FLEXPART-WRF models. To allow this an appropriate transition function based on $h/L$ has been proposed modulating the third moment of the turbulent velocity from zero, in near-neutral conditions, to its maximum allowed value in fully convective conditions. Following the approach currently used in FLEXPART (mainly for simplicity and computational efficiency) only a steady-state horizontally homogeneous drift term was included in the model but this was found to generate numerical instability when the steadiness and homogeneity conditions are significantly violated. To avoid this numerical instability, while still allowing the use of a steady and homogeneous drift formulation in unsteady and non-homogeneous conditions, a particle velocity re-initialization procedure similar to that previously used by Wilson and Yee (2000) was implemented. However, the use of a stationary and homogeneous drift term in conditions of unsteadiness and non-homogeneity produces systematic deviations in the results. In the present case, this error was discussed in detail for the unsteady case by running simplified test cases with varying stability and PBL height, and by comparing the results obtained with the correct non-stationary drift formulation with those obtained with the stationary drift. The deviation of particle density from the correct well-mixed state was observed to be between 5 and 10 % for $L$ linearly varying from $-20$ to $-400\,\hbox {m}$ during 380 s. Similarly, the deviation from the well-mixed state was between 5 and 10 % for the case of a CBL depth linearly decreasing to half of its initial height (2 km) during a period of 1 h and with $L=-20\hbox {m}$. The largest deviations from the well-mixed state were observed close to the top of the boundary layer while the deviations were minimal close to the bottom.

Systematic errors should be present to some extent in any steady and horizontally homogeneous drift formulation used in unsteady and/or horizontally non-homogeneous conditions. However, the present steady drift CBL formulation seems to be more sensitive to the non-stationary and non-homogeneous conditions than the steady drift Gaussian formulation, since numerical instabilities were observed in the current simulations while the standard Gaussian formulation used in FLEXPART did not show any numerical instability. As previously mentioned, Yee and Wilson (2007) discussed the general issue of “rogue trajectories” in the framework of Langevin models of particle velocity, which is a somewhat similar issue to that encountered here. They proposed a rather complex numerical scheme that may alleviate, if not eliminate, that problem. It may be possible that a more sophisticated numerical scheme would alleviate also the instability encountered here but this is not granted since the instability encountered here derives from an inconsistency between the drift formulation and the time-varying velocity statistics. For the present case, it would be more sensible to modify firstly the FLEXPART model so that time derivatives can be accounted for in the drift term.

Finally, using both FLEXPART and FLEXPART-WRF models, real-world numerical simulations have been performed under quite different convective conditions characterized by CBL depths ranging from about 1.3–4.5 km. These simulations showed that the effect of a vertical density gradient on particle dispersion in the CBL can be up to a maximum of about 10 % for a moderately deep (1.3–1.5 km) boundary layer but can be as much as about 15 % for a 3.2 km deep CBL, and more than 20 % in a very deep (4.5 km depth) boundary layer.

Appendices

Appendix 1

Assuming $m_A = M\sigma _A,\,m_B=M\sigma _B$ and defining $M=cS^{1/3}$ Luhar et al. (1996, 2000) report the following relationships connecting the standard deviation $(\sigma _w)$ and the skewness $(S)$ of the fluctuating component of the vertical velocity and all the variables $(A,\,B,\,m_A ,\,m_B ,\,\sigma _A ,\,\sigma _B )$ defining the turbulent vertical velocity PDF as a sum of two Gaussian PDFs,

$$\begin{aligned} \sigma _A&= \sigma _w \left( {\frac{B}{A(1+M^{2}}} \right) ^{1/2}, \end{aligned}$$

(23)

$$\begin{aligned} \sigma _B&= \sigma _w \left( {\frac{A}{B(1+M^{2}}} \right) ^{1/2}, \end{aligned}$$

(24)

$$\begin{aligned} A&= \frac{1}{2}\left[ {1-\left( {\frac{r}{4+r}} \right) ^{1/2}} \right] ,\end{aligned}$$

(25)

$$\begin{aligned} B&= 1-A, \end{aligned}$$

(26)

with

$$\begin{aligned} r=\frac{\left[ {(1+M^{2})^{3}S^{2}} \right] }{\left[ {(3+M^{2})^{2}M^{2}} \right] }. \end{aligned}$$

(27)

Appendix 2

For unstable conditions the standard deviation of the vertical velocity in the FLEXPART model is (http://transport.nilu.no/flexpart and http://flexpart.eu),

$$\begin{aligned} \sigma _w =\left( {1.2w_{*}^2 \left( {1-0.9\frac{z}{h}} \right) \left( {\frac{z}{h}} \right) ^{2/3}+(1.8-1.4\frac{z}{h})u_{*}^2 } \right) ^{1/2}+0.01. \end{aligned}$$

(28)

Considering Eq. 15 for the third moment and the general relationship (e.g. Stull 1988; Rodean 1996),

$$\begin{aligned} \frac{h}{L}=-k\frac{w_{*}^3 }{u_{*}^3}, \end{aligned}$$

(29)

where $k$ is the von Karman constant, it is possible to plot the value of the skewness and the value of the stability ratio $h/L$ for a range of values of $u_{*}$ and $w_{*}$. The skewness is also a function of the elevation above the ground $(z/h)$. The following Fig. 12 shows the variation of the stability parameter $h/L$, expressed as $-h/L$. Figure 13 shows the variation of the skewness without using any transition function, with the third moment from Eq. 12, as a function of $u_{*}$ and $w_{*}$, for various elevations $(z/h)$ above ground.

Fig. 12

Variation of the stability parameter $h/L,$ as a function of $u_{*}$ and $w_{*}$, and expressed as $-h/L$

Comparing Figs. 12 and 13, it can be seen that, for example, along the stability lines corresponding to $-h/L=1$ or $-h/L=10$, the skewness can assume values substantially different from zero. If a skewed PDF formulation is introduced for unstable conditions without a correction function in the third moment, only the stability threshold corresponding to $-h/L=0$ ensures a smooth change in the PDF. For any other threshold a discontinuity in the vertical velocity PDF arises with a sudden change from a Gaussian to a skewed PDF. The behaviour of the skewness is modified when a transition function is used in the third moment (e.g Eq. 14) as shown here in Fig. 14. It can be seen that the transition function ensures that the PDF changes from a Gaussian to a skewed formulation along the stability line $-h/L=5$ with a fully skewed PDF along the line $-h/L=15$.

Fig. 13

Skewness values without using any transition as a function of $u_{*}$ and $w_{*}$, for various scaled elevations $(z/h)$ above ground

Fig. 14

Skewness using the transition function in Eq. 14, as a function of $u_{*}$ and $w_{*}$, for various scaled elevations $(z/h)$ above ground