Derivation of Structure Parameters of Temperature and Humidity in the Convective Boundary Layer from Large-Eddy Simulations and Implications for the Interpretation of Scintillometer Observations

Abstract

We derive the turbulent structure parameters of temperature $C_{T}^2$ and humidity $C_q^2$ from high-resolution large-eddy simulations (LES) of a homogeneously-heated convective boundary layer. Boundary conditions and model forcing were derived from measurements at Cabauw in The Netherlands. Three different methods to obtain the structure-parameters from LES are investigated. The shape of the vertical structure-parameter profiles from all three methods compare well with former experimental and LES results. Depending on the method, deviations in the magnitude up to a factor of two are found and traced back to the effects of discretization and numerical dissipation of the advection scheme. Furthermore, we validate the LES data with airborne and large-aperture scintillometer (LAS) measurements at Cabauw. Virtual path measurements are used to study the variability of $C_{T}^2$ in the mixed layer and surface layer and its implications for airborne and LAS measurements. A high variability of $C_{T}^2$ along a given horizontal path in the LES data is associated with plumes (high values) and downdrafts (low values). The path average of $C_{T}^2$ varies rapidly in time due to the limited path length. The LES results suggest that measured path averages require sufficient temporal averaging and an adequate ratio of path length to height above the ground for the LAS in order to approach the domain average of $C_{T}^2$.

1 Introduction

A number of measurement systems have been used to observe the turbulence structure of the atmospherice boundary layer, including radars, sodars, lifted kites and aircraft (Petenko and Shurygin 1999; Muschinski 2004; Muschinski et al. 2004; Martin et al. 2010, among others). Recently, scintillometers have been increasingly employed to measure the optical interference along a horizontal path (e.g. Ochs and Wang 1978; Kohsiek 1982; Beyrich et al. 2002; among others). Scintillometers are operated in the atmospheric surface layer and consist of a wave transmitter and a receiver at both ends of a path that can cover several km. The transmitted waves that propagate through the atmosphere are affected by turbulent density fluctuations, so-called scintillations (Peltier and Wyngaard 1995). This scattering of the transmitted radiation is related to spatial fluctuations in the refractive index of air $n$. Tatarskii (1971) described this scattering theoretically using the refractive index structure function,

$$\begin{aligned} D_n(\mathbf x , \mathbf r , t) \equiv \{\left[n(\mathbf x ,t) - n(\mathbf x + \mathbf r ,t)\right]^2\}\ , \end{aligned}$$

(1)

where x and x + r are two points in space with displacement $r = |\mathbf r |$ at time $t$, and the curly brackets denote the ensemble average. If the displacement is in the inertial subrange of turbulence, the structure function can be expressed as

$$\begin{aligned} D_n = C_n^2 r^{2/3}\ , \end{aligned}$$

(2)

where $C_n^2$ is called the refractive index structure parameter. Under suitable conditions, scintillometer measurements may be traced back to the path mean $C_n^2$. Hill (1978) and Andreas (1988), among others, showed that $C_n^2$ is determined by the structure parameters of temperature, humidity and a joint structure parameter $C_{Tq}$, because variations in $n$ are dominantly caused by fluctuations in temperature $T$ and specific humidity $q$. Hill (1978) derived an expression for $C_n^2$ in terms of the structure parameters of meteorological variables, viz.

$$\begin{aligned} C_n^2 = \frac{A_{T}^2}{\{T\}^2} C_{T}^2 + 2\frac{A_{T}}{\{T\}}\frac{A_q}{\{q\}} C_{Tq} + \frac{A_q^2}{\{q\}^2} C_q^2, \end{aligned}$$

(3)

where the dimensionless coefficients $A_{T}$ and $A_q$ are functions of the wavelength $\lambda$ of the transmitted beam by the scintillometer, atmospheric pressure $p$, temperature and humidity (e.g. Hill et al. 1980).

Scintillometer observations have been frequently used to obtain horizontal path averages of $C_n^2$, and to deduce $C_{T}^2$ and $C_q^2$ from it, over typical distances of 5–10 km (e.g. Kohsiek et al. 2002; Meijninger et al. 2002a, b; Meijninger et al. 2006). So far, scintillometers are the only operational instruments that allow for estimating $C_{T}^2$ and $C_q^2$ at a spatial scale that might be representative for an area of several square km. Surface heterogeneity due to horizontal variations in soil moisture, vegetation and elevation, however, might affect the scintillometer measurements significantly. Footprint models for the scintillometer path can provide an estimate of its (heterogeneous) footprint. Nevertheless, it is difficult to validate these observations, particularly because usually only point measurements by, e.g. a sonic anemometer-thermometer/hygrometer system can be used for validation.

The surface fluxes of sensible and latent heat can be derived from the scintillometer measurements by means of Monin–Obukhov similarity theory (MOST). Some attempts have thus been made to validate scintillometer-derived fluxes by means of aggregated eddy-covariance measurements (Meijninger et al. 2002a, b; Meijninger et al. 2006), and Beyrich et al. (2006a) compared the structure parameters derived from scintillometer data to tower-based measurements. However, these studies have two major weaknesses: they compared path-averaged measurements with point measurements, and the effect of the surface heterogeneity could not be quantified. A few studies used airborne measurements that are generally representative of a larger area to validate scintillometer observations (Beyrich et al. 2006b; Moene et al. 2006). A first attempt has been made to use low-level aircraft flights along a scintillometer path during the LITFASS-2009 experiment (van den Kroonenberg et al. 2012, see also Beyrich et al. 2012). To the authors’ knowledge (also stated by Beyrich et al. 2012), it has not been possible so far to validate scintillometer-derived structure parameters against independent data representative of the same area.

There are few studies that have investigated structure parameters using large-eddy simulations (LES). Peltier and Wyngaard (1995) showed that LES can be employed to study the vertical distribution of the structure parameters in the convective boundary layer (CBL), and derived vertical profiles of $C_{T}^2,\,C_q^2$ and $C_{Tq}$, and showed that their LES data agree well with experimental results. Cheinet and Siebesma (2009) investigated the spatial variability of $C_{T}^2$ in the dry CBL with LES and showed the relation of the spatial variability of $C_{T}^2$ to the presence of ascending plumes. These updraft structures show a hexagonal cellular pattern near the surface, where the horizontal size of the cells scales with the boundary-layer depth $z_\mathrm{i}$ (Stull 1988). The vertical profiles of $C_{T}^2$ showed the decrease with height proposed by Kaimal et al. (1976), but Cheinet and Siebesma (2009) observed a gap of a factor two in the magnitude. Furthermore they found a bimodal distribution of $C_{T}^2$ near the surface, which was previously found in the sodar measurements of Petenko and Shurygin (1999). Cheinet and Cumin (2011) supplemented the previous LES studies by studying the variability of $C_q^2$. Cheinet and Siebesma (2007) used a wave propagation modeling framework to derive the scintillation rate and coherence length from virtual path measurements in their LES, and found that the variability of their virtual measurements of $C_n^{2}$ increased with height, while the path mean decreased. They stated that for their virtual paths (2 km length) it was not possible to provide representative estimates of $C_n^2$ with time averaging of 500 s. However, the coarse spatial resolution of 39 m in the horizontal and 32 m in the vertical direction did not allow the study of the wave propagation at realistic scintillometer heights, and no in situ scintillometer or aircraft measurements were used for comparison. Recently, Wilson and Fedorovich (2012) used LES to evaluate $C_n^2$ directly by calculating the refractive-index structure functions. They calculated the refractive index at each grid point and used Eq. 2, but they also employed Eq. 3 and calculated $C_{T}^2,\,C_q^2$ and $C_{Tq}$ from the fields of temperature and humidity. They could show that (for visible radiation) temperature contributes dominantly to $C_n^2$ in the lower half of the CBL, but that $C_{Tq}$ becomes important near the entrainment zone.

In the present paper we wish to gain more insight into the scintillometer technique by using the advantages of high-resolution LES that actually resolve the surface layer. The simulations are initialized by temperature and humidity profiles and driven by surface fluxes, derived from measurements during the RECAB¹ campaign at Cabauw in The Netherlands (de Arellano et al. 2004). Mean profiles of the structure parameters are derived from the LES data using different approaches, and validated for the first time directly with airborne and large-aperture scintillometer (LAS) measurements. Furthermore we extend the previous results of the LES study of Cheinet and Siebesma (2009) by calculating local structure parameters in order to investigate the effect of the temporal and spatial variability of $C_{T}^2$ in the CBL on aircraft and particularly LAS measurements. Virtual path measurements of the local $C_{T}^2$ are then used for studying the representativeness of in situ measurements.

The paper is organized as follows: Sect. 2 deals with different methods to derive structure parameters, while Sect. 3 gives a case description, including synoptic conditions, the LES set-up and data processing. Results are presented in Sect. 4, and in Sect. 5 we discuss and summarize our results.

2 Derivation of Structure Parameters from LES

Different approaches to determining structure parameters from turbulence data have been proposed in the literature. In this section we outline three different methods that can be applied to LES data in order to obtain vertical profiles of $C_{T}^2$ (here for potential temperature) and $C_q^2$ (for specific humidity). As estimates of the surface fluxes of sensible and latent heat can be calculated from $C_{T}^2$ and $C_q^2$ by means of MOST, these two structure parameters are of most practical interest. All of these methods are based on Kolmogorov’s similarity hypotheses for the turbulence spectra.

2.1 Structure Parameters from Turbulence Spectra

The structure parameters $C_{T}^2,\,C_q^2$ and $C_{Tq}$ are directly proportional to the spectra of temperature, humidity and their cospectrum in the inertial subrange, respectively. Wyngaard et al. (1971b) related the structure parameter of the scalar $S$ (temperature or humidity) at a given height to the power spectral density $\varPhi _S$ by

$$\begin{aligned} C_{S,\mathrm{G}}^2 = \frac{1}{0.2489} \varPhi _S (k) k^{5/3}, \end{aligned}$$

(4)

where $k$ is a wavenumber in the inertial subrange (slope $\varPhi _S \sim k^{-5/3}$) and $0.2489 = 2/3\varGamma (1/3)$ after Muschinski et al. (2004). The subscript G indicates that this method derives global values of $C_S^2$ (i.e. horizontally-averaged values). Since this method directly derives the structure parameters from the turbulence spectra, we hereafter refer to this method as the spectral method.

2.2 Structure Parameters from (Local) Dissipation Rates

In the inertial subrange the power spectral density is proportional to the $2/3$ power of the dissipation rate $\varepsilon$ of turbulent kinetic energy (TKE) and can be calculated after Tennekes and Lumley (1973) by

$$\begin{aligned} \varPhi _{u,v}(k)&= \alpha \ \varepsilon _{\mathrm{TKE, G}}^{2/3}\ k^{-5/3},\end{aligned}$$

(5)

$$\begin{aligned} \varPhi _{w}(k)&= \frac{4}{3}\ \alpha \ \varepsilon _{\mathrm{TKE, G}}^{2/3}\ k^{-5/3}, \end{aligned}$$

(6)

where $\alpha \approx 0.52$ is the Kolmogorov constant and $u,\,v$ and $w$ are the velocity components on a Cartesian coordinate system. Corrsin (1951) showed that the power spectral density of temperature is related to the dissipation of temperature variance $\varepsilon _{T}$ and TKE $\varepsilon _\mathrm{TKE}$. Generalized for any scalar quantity, this relation reads

$$\begin{aligned} \varPhi _S(k) = \beta \ \varepsilon _\mathrm{TKE,G}^{-1/3}\ \varepsilon _{S,\mathrm{G}}\ k^{-5/3}\ , \end{aligned}$$

(7)

where $\beta \approx 0.4$ is the Obukhov–Corrsin constant (Sreenivasan 1996). A derivation of $\varepsilon _{S,\mathrm{G}}$ from the turbulence spectra follows from substitution of $\varepsilon _{\mathrm{TKE, G}}$ into Eq. 7 with Eqs. 5–6. Substituting $\varPhi _S$ in Eq. 4 with Eq. 7 yields an expression that relates the structure parameters of a scalar quantity to the dissipation rates of TKE and scalar fluctuations (Wyngaard and LeMone 1980; Peltier and Wyngaard 1995),

$$\begin{aligned} C_{S,\mathrm{G}}^2 = \frac{\beta }{0.2489}\ \varepsilon _\mathrm{TKE, G}^{-1/3}\ \varepsilon _{S,\mathrm{G}}. \end{aligned}$$

(8)

The structure parameter can be regarded as a local and instantaneous quantity. It can be defined through the average over a small volume in the inertial subrange and it is thus possible to rewrite Eq. 8 after Cheinet and Siebesma (2009) in terms of local dissipation rates,

$$\begin{aligned} C_{S,\Delta \mathbf x }^2(\mathbf x ,t) = \frac{\beta }{0.2489}\ \varepsilon _{\mathrm{TKE},\Delta \mathbf x }^{-1/3}(\mathbf x ,t)\ \varepsilon _{S,\Delta \mathbf x }(\mathbf x ,t)\ , \end{aligned}$$

(9)

where $\Delta \mathbf x$ denotes the size of the volume. Since the above equation allows the calculation of $C_{S,\Delta \mathbf x }^2$ by means of the dissipation rates only, this method is hereafter referred to as the dissipation method. Cheinet and Siebesma (2009) discussed that the empirical constant $\beta$ might not be well-determined, but we follow their choice and use the widespread value of $\beta = 0.4$.

In LES the turbulent eddies are directly resolved down to the truncation size $\varDelta$, which is assumed to be located in the inertial subrange, whereas eddies smaller than $\varDelta$ are parametrized within the subgrid-scale (SGS) model. The used LES model employs implicit filtering so that the nominal truncation size is determined by the grid resolution (see below). In practice, however, the SGS model affects to some extent also eddies that are larger than $\varDelta$. The actual truncation size is thus not sharp and located at larger scales than $\varDelta$. We follow Cheinet and Siebesma (2009) and relate the local dissipation rate of TKE to the SGS parametrization in the LES model. In the LES model PALM (Raasch and Schröter 2001), $\varepsilon _{\mathrm{TKE},\Delta \mathbf x }$ for a grid volume is calculated very similarly to the DALES model (Heus et al. 2010), used by Cheinet and Siebesma (2009) and going back to Deardorff (1980), as

$$\begin{aligned} \varepsilon _{\mathrm{TKE},\Delta \mathbf x } = \left(0.19 + 0.74 \frac{l}{\varDelta }\right) \frac{e^{3/2}}{l}\ , \end{aligned}$$

(10)

where $\varDelta = \root 3 \of {\varDelta _x \varDelta _y \varDelta _z} = \root 3 \of {\Delta \mathbf x }$ with $\varDelta _x, \varDelta _y$ and $\varDelta _z$ being the grid resolutions of the Cartesian coordinate system $(x,y,z),\,e$ is the subgrid-scale TKE (also refered to as SGS-TKE). The subgrid-scale mixing length $l$ depends on height and stratification; in unstable stratification $l$ usually equals $\varDelta$, whereas $l$ becomes smaller in stably stratified regions (Deardorff 1980). The local dissipation of scalar fluctuations can be modelled using the local budget, equating dissipation and mean-gradient production (Cheinet and Siebesma 2009; see also Peltier and Wyngaard 1995), viz.

$$\begin{aligned} \varepsilon _{S,\Delta \mathbf x } = 2 K_S \left( \frac{\partial S}{\partial x_i} \right)^2\ , \end{aligned}$$

(11)

where $K_S$ is the local SGS eddy diffusivity of the scalar, which is related to the SGS-TKE in the used SGS model as follows (see also Sect. 3.3):

$$\begin{aligned} K_S = K_\mathrm{m} \left( 1 + \frac{2l}{\varDelta } \right) = c_\mathrm{m} l \left(1 + \frac{2l}{\varDelta } \right) \sqrt{e}, \end{aligned}$$

(12)

where $K_\mathrm{m} \!=\! c_\mathrm{m} l \sqrt{e}$ is the SGS eddy diffusivity of momentum and $c_\mathrm{m} = 0.1$ is a model constant. Equation 9 can thus be written in terms of the SGS model parametrization above as

$$\begin{aligned} C_{S,\Delta \mathbf x }^2 = \frac{0.2\ \beta }{0.2489} l^{4/3} \left( 1 + \frac{2l}{\varDelta } \right) \left( 0.19 + 0.74 \frac{l}{\varDelta } \right)^{-1/3} \left( \frac{\partial S}{\partial x_i} \right)^2\ , \end{aligned}$$

(13)

where the SGS-TKE has cancelled out (cf. Cheinet and Siebesma 2009, Eq. 8).

2.3 Structure Parameters from Wavelet Analysis

As shown in Sect. 2.1 the scalar structure parameter can be derived from the inertial subrange in the scalar Fourier spectrum. A drawback of this method is that the Fourier spectrum is a global quantity, yielding a global estimate of the structure parameter. However, using a wavelet spectrum (derived from the continuous wavelet transform at a given location in space) one can determine the local spectrum from which a local estimate of the structure parameter can be derived (see Moene and Gioli 2008). As long as an identifiable inertial subrange is present in the local wavelet spectrum, the relationship between the Fourier spectrum and the structure parameter should be locally retained.

The local structure parameters can be calculated from Eq. 4 by substituting $\varPhi _S$ with its local estimate,

$$\begin{aligned} C_{S,\Delta k}^2(x_m) = \frac{1}{0.2489}\ \varPhi _S(x_m,k)\ k^{5/3}\ , \end{aligned}$$

(14)

where $\Delta k$ indicates the spectral range over which $\varPhi _S$ is averaged (see below); $x_m$ is the discrete series in space at the location $m$ (see also Torrence and Compo 1998). For the wavelet function we use the Morlet wavelet with non-dimensional frequency six as it reproduces, when integrated over the entire series, an optimum Fourier spectrum. Furthermore it provides a good balance between locality in space and time (Grinsted et al. 2004). The Fourier equivalent wavelength for this wavelet is $1.03$ times the scale of the wavelet (see Torrence and Compo 1998).

The smallest scales in a wavelet transform contain the most localized information, whereas increasingly larger scales of the wavelet transform use information from increasingly larger sections of the data. Hence it would be tempting to apply Eq. 14 to the smallest scale of the spectrum. However, then one needs to be sure that this scale is within the inertial subrange. Furthermore, the variance in the wavelet spectrum is usually high. Therefore, spectral and spatial averaging is applied to Eq. 14 between the smallest scales located inside the inertial subrange and some larger scale that is chosen such that the required spatial information is still retained. This spectral averaging implies also additional implicit spatial averaging. The larger the used spectral scales, the larger is the spatial average. e.g. if spectral scales around 100 m are averaged, this would imply a spatial averaging in the order of 100 m. The index $\Delta k$ refers to this spectral/spatial averaging.

3 Case Description and LES Model

3.1 Case Description

We use measurements from the RECAB data, observed on 27 July 2002 at Cabauw. The Cabauw area is flat and fairly homogeneous, with terrain being mainly open pasture, crossed by ditches, windbreaks, small built-up areas and the river Lek. The prominent feature of the site is a 213-m high tower constructed for meteorological research. Low geostrophic wind speeds and a cloudless sky were observed at least until 1400 UTC, proving suitable conditions for the simulation of a free-convective boundary layer. After 1400 UTC, scattered cumulus clouds were observed. Due to intense precipitation on the previous day, the near-surface Bowen ratio $B_0$ was 0.3–0.4, with $B_0$ defined as

$$\begin{aligned} B_0 = \frac{c_\mathrm{p}\overline{w^{\prime }\theta ^{\prime }_0}}{L_\mathrm{v}\overline{w^{\prime }q^{\prime }_0}}, \end{aligned}$$

(15)

and where $c_\mathrm{p}$ is the specific heat at constant pressure and $L_\mathrm{v}$ is the latent heat of vaporization; $\overline{w^{\prime }\theta ^{\prime }_0}$ and $\overline{w^{\prime }q^{\prime }_0}$ are the kinematic surface fluxes of sensible and latent heat, respectively. The boundary-layer depth increased from 353 m at 0816 UTC to 955 m at 1249 UTC. For a detailed description of the conditions during the experiment see de Arellano et al. (2004).

3.2 Observations at Cabauw

Surface fluxes of sensible and latent heat were measured next to the Cabauw tower at 5.37 m by means of the eddy-covariance technique. These fluxes were used as lower boundary conditions for the large-eddy simulations. Additionally, airborne observations of the Sky Arrow ERA aircraft platform (Gioli et al. 2006) were available; the aircraft had a cruise flight speed of 49 m s$^{-1}$ and recorded temperature and humidity at 50 Hz. Moreover, de Arellano et al. (2004) computed the high frequency attenuation for these specific temperature and humidity sensors and found that signals were not attenuated below 10 and 15 Hz respectively. From a spectral analysis we found that spatial fluctuations at a scale of 10 and 5 m could be resolved for temperature and humidity, respectively. There were two measurement periods: in the morning between $0745$ and 0911 UTC and in the afternoon between $1230$ and 1355 UTC. During spiral flights, vertical profiles of temperature and humidity were measured, and were used for the initialization and validation of the respective LES profiles. Horizontal flight legs of about 10 km were flown repeatedly at different heights over short grassland, with 3–7 (typically four) repetitions flown at three different height levels. In the morning these height levels were at 79, 167 and 257 m, while in the afternoon flights were performed at 79, 261 and 625 m above the ground. The flight legs were designed to coincide with the path of an LAS, which measured $C_n^2$ at an average path height of 41 m. Since the LAS uses a radiation source in the near-infrared wavelength range, it is mainly sensitive to $C_{T}^2$ (Kohsiek et al. 2002).

The database was supplemented by a UHF wind profiler, for estimating $z_\mathrm{i}$, and the Cabauw tower with measurement equipment mounted at different heights. A more detailed description of the measurements and Cabauw site characteristics is given in de Arellano et al. (2004) and Kohsiek et al. (2002).

3.3 LES Model and Simulation Set-Up

The PArallelized LES Model (PALM, Raasch and Schröter 2001) was used for the present study, and has been widely applied to study different flow regimes in the convective boundary layer (e.g. Raasch and Franke 2011; Maronga and Raasch 2013). All simulations were carried out using cyclic lateral boundaries. A staggered grid is used, where scalar quantities are defined at the centre of the grid volumes, whereas velocities are defined on the lateral faces of the volumes. The grid was stretched in the vertical direction well above the top of the boundary layer to minimize computational time in the free atmosphere. MOST was applied locally between the surface and the first computational grid level, including the calculation of the local friction velocity $u_*$. A 1.5-order flux-gradient subgrid closure scheme, after Deardorff (1980), was applied, which requires the solution of an additional prognostic equation for the SGS-TKE. The SGS model contains a diagnostic relation for the SGS-TKE dissipation rate (see Eq. 10). A fifth-order advection scheme of Wicker and Skamarock (2002, hereafterWS-5) was used in this study. Moreover, the second-order scheme after Piacsek and Williams (1970, hereafter PW-2) was chosen for comparative simulations.

Based on the Sky Arrow measurement periods we carried out both a morning and an afternoon simulation (cases M and A, respectively), where each simulation was driven by constant surface fluxes of sensible and latent heat, derived from the eddy-covariance measurements at Cabauw. Despite the fact that the observed surface fluxes displayed a diurnal cycle (see de Arellano et al. 2004), we decided to use constant fluxes, because in this way we could reach a quasi-stationary state in both simulations in short time. Neutrally-stratified initial profiles of temperature $(\theta _0)$ and humidity $(q_0)$ with a capping inversion above were prescribed in such a way that the mean LES profiles after 1 h of simulation time matched the spiral vertical aircraft flights and tower measurements around 0816 UTC and 1249 UTC, respectively (see also Fig. 1). Additionally an aerodynamic roughness length of 0.1 m was prescribed at the surface. Since only wind speeds $<$3 m s$^{-1}$ were observed, no mean flow was prescribed in the simulation (free convective conditions). The initial settings are listed in Table 1.

Table 1 LES grid set-up and initial parameters

Fig. 1

Domain-averaged profiles of potential temperature (left) and specific humidity (right) for cases M (a, b) and A (c, d). Spiral aircraft flights (grey) started at 0812 UTC and 0816 UTC (case M) as well as at 1245 UTC (case A)

The model was discretized in space with 1,024 grid points in each horizontal direction; the grid resolution in case M was 2 m in all spatial directions ($\varDelta _x = \varDelta _y = \varDelta _z = 2$m) and $448$ grid points were used in the vertical direction. In case A, owing to the considerably larger boundary-layer depth, a sufficiently large horizontal domain was necessary in order to capture all relevant turbulent scales (see Sect. 3.1). Hence we used a horizontal grid resolution of 4 m. In the vertical direction 832 grid points were used with $\varDelta _z = 2$ m, and both simulations lasted 2 h with a constant timestep of 0.25 s. For studying the representativeness of LAS measurements (see Sect. 4.6) two additional simulations (cases ME and AE) with an extended model domain in the $x$-direction were carried out. The domain sizes for all four simulations are given in Table 1.

3.4 Derivation of Structure Parameters from the Different Data Sources

3.4.1 LES Data

In Sect. 2 we introduced different methods for obtaining $C_{T}^2$ and $C_q^2$. In order to compare the different methods we calculated domain-averaged vertical profiles of the structure parameters by means of the spectral, dissipation and wavelet methods.

The turbulence spectra were calculated from three-dimensional LES data of temperature and humidity. First we calculated all one-dimensional spectra in the $x$- and $y$-directions for each horizontal plane, and these spectra were subsequently averaged. Second, we performed a quality check following Hartogensis and De Bruin (2005) to determine whether an inertial subrange was present in the spectrum. This check basically tests small block intervals of the spectrum to determine whether they follow the $-5/3$ power law and whether the variance in these intervals is sufficiently small. If less than $30\,\%$ of the wavenumbers in the spectrum are found to be the inertial subrange, a missing value was inserted. This occured only sporadically well above the capping inversion and hence did not affect our results. Thirdly, we calculated the structure parameters at the height of each plane by calculating $C_{S,\mathrm{G}}^2(k)$ by means of Eq. 4 for all $k$ in the inertial subrange and subsequent spectral averaging. The largest wavenumber in the inertial subrange usually depends on the grid resolution and was typically found to be at $k \approx 2\pi /6\varDelta _{x,y}$ (equivalent to scales of $6\varDelta _{x,y}$) throughout the surface layer and boundary layer. The largest scales (smallest wavenumbers) were typically in the order of several hundreds of metres.

The local structure parameters $C_{S,\Delta \mathbf x }^2$ were calculated on-the-fly during the simulation according to the described dissipation method (see Eq. 13) using the three-dimensional fields of temperature and humidity. The gradients in Eq. 13 are approximated using central finite differences on the LES grid. The global values $C_{S,\mathrm{G}}^2$ were calculated by the horizontal averaging of $C_{S,\Delta \mathbf x }^2$.

For the wavelet method we first obtained the local Fourier spectrum from one-dimensional wavelet transforms, using the smallest resolved scale in the LES $(2\varDelta _{x,y})$ as the smallest scale of the wavelet. We calculated all one-dimensional local spectra in the $x$- and $y$-directions for each horizontal plane, and these local spectra were subsequently averaged. Second, we determined $C_{S}^2$ as a function of $k$ (Eq. 14) for each one-dimensional series in each horizontal plane (first in one direction, then in the orthogonal direction). Due to high variability in the local Fourier spectra it was not possible to determine a local inertial subrange. Third, we thus spatially averaged all local Fourier spectra. In this way we could determine an inertial subrange, which we found to usually cover wavenumbers from $k \approx 2\pi /6\varDelta _{x,y}$ to an upper limit $k \approx 0.06$ m$^{-1}$. Fourth, we used this calculated wavenumber range to apply a spectral averaging on the $C_{S}^2$ values from the local spectra (yields $C_{S,\Delta k}^2$). Note that, due to the nature of the wavelet spectrum, the large-scale end of the inertial subrange takes into account larger spatial scales than the small-scale end (see Sect. 2.3). The local structure parameters are thus to some extent artificially smoothed, but this does not affect their global mean values. In order to determine vertical mean profiles $(C_{S,\mathrm{G}}^2)$ we first performed steps one and three. Then we calculated $C_{S}^2$ as a function of $k$ from the averaged spectrum followed by spectral averaging.

For convenience we will hereafter omit the subscript indices (G, $\Delta \mathbf x ,\,\Delta k$).

3.4.2 Aircraft Data

The wavelet method was used to obtain $C_{T}^2$ and $C_q^2$ from the horizontal flight legs of the Sky Arrow aircraft. The time series of temperature and humidity along the flight legs were first converted to an equidistant space series using the geo-location of the points (linear interpolation was used). The spatial resolution was equal to the mean spatial resolution of the original time series (approximately 1 m). Next the wavelet spectrum was calculated for each point in the spatial series, and the local estimates of $C_S^2(x_m,k)$ were derived from Eq. 14. The smallest scale to be used for the spectral averaging was determined by verifying that the leg-averaged structure parameter was independent of the choice of the smallest scale (this turned out to be 50 m), and the largest scale was selected to be 208 m. The spectral filtering implies as well a spatial filtering. By choosing larger spectral ranges, the variability along the flight legs is thus significantly decreased. The structure parameter was spatially averaged over a running window of 20 m and stored at a spatial interval of 5 m for every 5 m in the flight leg. For validation of the LES profiles, the local $C_S^2$ estimates were averaged over their full flight legs.

3.4.3 LAS Data

Temporally-averaged values (10 min) of $C_n^2$ were obtained from the LAS at Cabauw. The relationship between $C_n^2$ and $C_{T}^2,\,C_q^2$, and $C_{Tq}$ was already given in Eq. 3. The importance of $T$ and $q$ on $C_n^2$, however, depends on the wavelength of the radiation used. An optical LAS is mainly sensitive to temperature fluctuations, and if no second scintillometer, operating at a wavelength sensitive to humidity, is available, only little information can be obtained on $C_{Tq}$ and $C_q^2$ (Moene 2003). It is common to eliminate $C_{Tq}$ and $C_q^2$ by using the available information about the relationship between temperature and humidity, namely by applying a correction involving the Bowen ratio $B$. We use the approximation discussed in Moene (2003) to relate $C_n^2$ to $C_{T}^2$ with a Bowen ratio correction term,

$$\begin{aligned} C_n^2 \approx \frac{A_{T}^2}{\overline{T}^2}C_{T}^2\left(1 + \frac{A_q}{\overline{q}}\frac{\overline{T}}{A_{T}}\frac{c_\mathrm{p}}{L_\mathrm{v}}B^{-1}\right)^2. \end{aligned}$$

(16)

The temporally-averaged temperature $\overline{T}$ and humidity $\overline{q}$ were determined from observations at the Cabauw mast at a height of 40 m and thus close to the level of the LAS; $A_{T},\,A_q$ are functions of $T$ and $q$ and the transmitted wavelength of the LAS ($\lambda$ $=$ 940 nm) (Hill et al. 1980). The Bowen ratio at the height of the LAS was not available. As the flux divergence may be significant and different for sensible and latent heat, particularly in morning conditions, we derived $B$ at a height of 41 m from the LES data instead. Since the measured surface fluxes (and thus $B_0$) were prescribed, we expect that the LES will provide a realistic estimate of the Bowen ratio at the scintillometer height.

3.4.4 Virtual Path Measurements in LES—An Embedded Virtual LAS

In order to study the variability along a measurement path and the variability of the path average, we employ the dissipation method and use virtual measurements along horizontal paths within our LES domain. By doing so, we capture the turbulent fluctuations, represented by the local structure parameter of temperature, as they would be seen from LAS and aircraft. However, on the one hand, the scintillations seen by the LAS are mainly determined by fluctuations at the scale of the beam diameter (0.31 m), while smaller scales are averaged out. Larger scales result in variability of the scintillations. On the other hand, the nominal truncation size is 2–4 m (the actual truncation happens at even larger scales up to $6\varDelta _{x,y}$) and hence there is a part of the variability in the structure parameters that is missed by the LES (see Cheinet and Siebesma 2009, Fig. 8).

In contrast to previous studies, the present LES allow for studying the structure parameters in the surface layer, where LAS are typically operated. Path averaging of $C_{T}^2$ can be done in two ways. In order to simulate LAS data, the path-weighted average after Wang et al. (1978) is used (see Fig. 9 and Appendix). These virtual LAS (hereafter VLAS) measurements are denoted by $\langle \widetilde{C_{T}^2} \rangle _\mathrm{p}$. In order to simulate aircraft data, a simple arithmetic average is used (denoted by $\langle C_{T}^2 \rangle _\mathrm{p}$).

VLAS measurements are used at typical height levels of LAS measurements between 30 and 70 m above the ground. Additionally we carried out virtual measurements without a weighting function at heights close to the aircraft flights at Cabauw (79, 167, 257, 261 and 625 m, depending on time of the day). In order to study long paths, we carried out the additional simulation cases ME and AE with extended horizontal domains in the $x$-direction (see Table 1). The virtual measurements were carried out in this extended $x$-direction. The maximum possible path length was 10.24 and 11.52 km for case ME and AE, respectively, and thus covered the LAS path at Cabauw as well as the aircraft flight legs. Overall we had at least 1,024 paths available for each virtual measurement height. The mean over all VLAS paths in one plane differs slightly from the horizontal mean due to the path weighting. We analyzed the data after 2 h of simulation time and used one-sided causal time averaging based only on past timesteps during the period from 1 to 2 h.

3.4.5 Synopsis of the Data Processing

In order to derive the structure parameters from the different methods, several averaging procedures are applied; this includes spatial, spectral and temporal averages. In Sect. 4 we use all three methods in order to compare the mean profiles of $C_S^2$. Two methods for the LES data provide local estimates of $C_S^2$ that will be mutually compared (dissipation and wavelet method). One method will be used to compare the variability of $C_S^2$ with measurement data (dissipation method). The used averaging types are summarized in Table 2, and the respective averaging scales and ranges are given in Sects. 3.4.1–3.4.4.

Table 2 Synopsis of basic averaging types that have been applied and for which figures the methods have been used

4 Results

4.1 Temperature and Humidity Profiles

The horizontally-averaged (denoted by $\langle \;\;\rangle$) profiles of temperature and humidity from the LES and aircraft observations are shown in Fig. 1. The LES profiles reveal classical CBL profiles with unstable stratification near the surface, a well-mixed layer, a stably-stratified layer in the entrainment zone and in the free atmosphere aloft. As shown in Fig. 1a, the simulated mixed-layer temperature is slightly higher (on average 0.3 K) after 1 h than the observed aircraft profile. Specific humidity is slightly overestimated by the LES as well. The boundary-layer depth in case M is 364 m, which is close to that observed by the aircraft; Fig. 1c, d (case A) reveals a boundary-layer depth of about 1,000 m and negligible deviations between LES and aircraft measurements, except for the humidity in the entrainment zone. Here the aircraft data suggest a smaller humidity jump and an entrainment ratio around zero (see de Arellano et al. 2004, Fig. 4b). We checked the humidity flux profile in the LES and found an entrainment ratio around $0.2$, which is at least close to zero. Additionally, de Arellano et al. (2004) gave the mixed-layer velocity scale $w_* = \left[\left(g/\overline{\theta }\right)\ \overline{w^{\prime }\theta ^{\prime }_0}\ z_\mathrm{i}\right]^{1/3}$ (with $g$ being the gravitational acceleration), which was 0.94 and 1.44 m s$^{-1}$ between 0816–0905 UTC and 1249–1342 UTC, respectively. Due to the similar boundary-layer depth in the observations and LES, $w_*$ from the LES was also similar to the observational value, with 0.89 m s$^{-1}$in case M and 1.33 m s$^{-1}$ in case A after 1 h of simulation (see Table 3). We can thus essentially assume that the LES generated a CBL similar to that observed at Cabauw. The measurements of $C_{T}^2$ and $C_q^2$ by aircraft and LAS should thus be comparable to the derived structure parameters from the LES data.

4.2 Structure Parameter Profiles

Figure 2 shows the mean vertical profiles of $C_{T}^2$ and $C_q^2$ for cases M and A after 1 h of simulation calculated by the different methods; aircraft and LAS data were added. Normalization has been applied according to Burk (1981) using $z_\mathrm{i}$ and the mixed-layer temperature and humidity scales after Deardorff (1974): $\theta _* = \overline{w^{\prime }\theta ^{\prime }_0} / w_*$ and $q_* = \overline{w^{\prime }q^{\prime }_0} / w_*$ (see also Table 3),

$$\begin{aligned} C_{T,*}^2&= \frac{\theta _*^2}{z_\mathrm{i}^{2/3}}\;,\end{aligned}$$

(17a)

$$\begin{aligned} C_{q,*}^2&= \frac{q_*^2}{z_\mathrm{i}^{2/3}}. \end{aligned}$$

(17b)

4.2.1 LES Profiles

The profiles of $C_{T}^2$ (Fig. 2a,c) are characterized by high values of $C_{T}^2$ close to the surface that are caused by large temperature gradients that lead to a large production of temperature variance and hence to an increase in the energy level in the inertial subrange. $C_{T}^2$ decreases in the mixed layer according to $F_{T} (z/z_\mathrm{i})^{-4/3}$ up to a height of $z/z_\mathrm{i} = 0.6$ as proposed in theory (Wyngaard and LeMone 1980); here, $F_{T}$ is a proportionality constant. Above, entrainment processes dominate and a secondary peak is present in the entrainment zone, where sharp local temperature gradients between the free atmosphere and the boundary layer lead to a high production of temperature variance.

When entrainment effects are negligible, $C_q^2$ should follow $F_{q} (z/z_\mathrm{i})^{-4/3}$, at least in the lower boundary layer (Fairall 1987). As shown in Fig. 2b,d, a minimum is located at $z/z_\mathrm{i} = 0.3$ and increasing values with height are found, which are caused by high humidity fluctuations in the upper boundary layer due to the entrainment of dry air from the free atmosphere (Peltier and Wyngaard 1995). It is evident that all three calculation methods show these general shapes, which are in agreement with theory (Wyngaard et al. 1971a, b), the semi-empirical profiles after Kaimal et al. (1976) and Fairall (1987), observations (e.g. Wyngaard and LeMone 1980; Kohsiek 1988) and the recent LES of Cheinet and Siebesma (2009) and Cheinet and Cumin (2011).

Table 3 Scaling parameters for cases M and A

Fig. 2

Normalized profiles of $C_{T}^2$ and $C_q^2$ after 1 h of simulation time, derived from different methods, and on a logarithmic scale. Aircraft ($\times$ symbols) and LAS ($+$ symbols, red) measurements as well as the semi-empirical profile after Kaimal et al. (1976) (dashed black line) are included. Similarity relationships are given for the spectral method (solid black lines)

The magnitude of $C_{T}^2$ in the mixed layer from the spectral method is $20\,\%$ lower than the semi-empirical profile of Kaimal et al. (1976). Since $C_{T}^2$ depends only on the power spectral density, the LES obviously renders proper energy levels in the inertial subrange of CBL spectra (respective spectra will be shown and discussed in Sect. 4.5). Therefore, we will hereafter use the spectral method as a reference for the other two methods. The proportionality constant $F_{T}$, however, is $\approx 1.9$ and thus lower than the value of $2.7$ proposed by Wyngaard and LeMone (1980). The dissipation method shows lower values in $C_{T}^2$ compared to the spectral method by a factor of $1.7$. Cheinet and Siebesma (2009) found a gap of a factor $2$ between the dissipation method and the profile of Kaimal et al. (1976). Our results support their finding and we will address this underestimation of the structure parameters by the dissipation method in Sect. 4.5. The wavelet method shows values similar to the spectral method.

In case M, $C_q^2$ shows lower values than suggested by the semi-empirical profile after Fairall (1987), whereas in case A, $C_q^2$ (spectral method) is in remarkable agreement with Fairall (1987). In the lower boundary layer, $C_q^2$ (Fig. 2b,d) follows the expected decrease with $F_q \approx 2.3$, which is higher than suggested by Wyngaard and LeMone (1980). They also state that differences between $F_{T}$ and $F_q$ can be ascribed to differing surface transfer processes of the active scalar temperature and the more or less passive scalar humidity. In case M, the peak of $C_q^2$ at the top of the mixed layer is greater than that of $C_{T}^2$, whereas the peak values are similar for case A. This seems consistent with the fact that the entrainment ratio for $q$ is around $1.3$ for case M and around $0.2$ for case A (cf. de Arellano et al. 2004, Fig. 4). This implies that the profile of the humidity variance differs significantly from the profile of temperature variance (see Moene et al. 2006 and Sect. 4.3.1) and hence also the dissipation rates. For $C_q^2$ we observe a gap of $1.8$ between the spectral and dissipation methods, whereas the spectral and wavelet methods give very similar profiles.

4.2.2 Validation of the LES Profiles with Cabauw Observations

$C_{T}^2$ shows very good agreement between the LES and LAS in case M (Fig. 2a, c). The spectral method compares well to the low-level flights, but the aircraft data do not show the decrease with height as proposed by Kaimal et al. (1976), leading to a significant underestimation of $C_{T}^2$ in the LES at heights above $z/z_\mathrm{i} = 0.4$. In case A, the LES slightly overestimates $C_{T}^2$ from the low-level flights, while the LES compares well to three of the four medium-level flights at $z/z_\mathrm{i} = 0.27$. The higher-level flights again suggest an underestimation in $C_{T}^2$ by the LES. It appears that $C_{T}^2$ compares well with the aircraft data between $z/z_\mathrm{i} = 0.2$ and $z/z_\mathrm{i} = 0.3$, and below these heights $C_{T}^2$ is overestimated. Above, the LES data show an underestimation of $C_{T}^2$. A possible reason for this discrepance might be the fact that we assumed free convective conditions, whereas the observations are made in light winds. Thus in reality there may be wind shear across the entrainment zone that leads to extra scalar variance and hence higher $C_{T}^2$. In addition, mesoscale fluctuations in advected scalars (here temperature) may yield an extra production of variance as shown by Kimmel et al. (2002). Such effects of shear and advection might generally also apply to $C_q^2$. As will be discussed in Sect. 4.6.3, the aircraft measurements suffer from a statistical uncertainty of about 10–20 % (shown for $C_{T}^2$), which has to be considered as well.

The structure parameter for humidity in the LES data is in much better agreement with the aircraft observations (see Fig. 2b, d). Despite a tendency for a higher $C_q^2$, the LES profile agrees well with the aircraft data, particularly for case M. The decrease with height is reproduced well by the LES. For case A, the LES (spectral method) values agree with two of the three high-level flights at $z/z_\mathrm{i} = 0.65$, while at the other levels the aircraft data are below the LES values. The statistical uncertainty for aircraft measurements (see Sect. 4.6.3) are shown for $C_{T}^2$, but an uncertainty of 10–20 % was obtained for $C_q$ as well.

4.3 Spatial Variability of Structure Parameters

4.3.1 LES Results

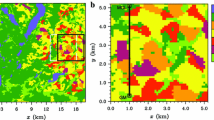
Cheinet and Siebesma (2009) investigated the spatial variability of $C_{T}^2$ from the dissipation method. Our analysis reproduces their findings and we found similar characteristics for $C_{T}^2$ and $C_q^2$, which is the reason we limit ourselves to a discussion of $C_{T}^2$ in detail. For example, in Fig. 3a a horizontal cross-section of $C_{T}^2$ at 41 m (LAS height) is shown for case M, derived with the dissipation method. The flow circulation generates a cellular pattern of $C_{T}^2$ with high values at the edges of the cells. Figure 3b shows the respective pattern, derived from the wavelet method. Generally, the dissipation and wavelet methods generate the same structure-parameter pattern. The fact that even the smallest structures are reproduced in both patterns is a remarkable feature and emphasizes that both methods correlate well. However, one might prefer the wavelet method simply because it neither depends directly on the SGS model nor on the parameter $\beta$. Both methods also show significant differences: due to generally too low values produced by the dissipation method, the maximum values coincide ($3.21$ and $3.43$ for wavelet and dissipation methods, respectively), whereas minimum values differ significantly ($-1.84$ and $-7.80$). Note that the range of values for the wavelet method strongly depends on the spectral averaging range, which was 13–106 m in this case; this applies also to spatial averaging. A direct comparison with the dissipation method is thus challenging.

Unfortunately we found that the wavelet method required a very large computing time in order to calculate a single horizontal cross-section. Furthermore, it is to some extent sensitive to changes of parameters, such as wavelet scale and the chosen averaging window. It was thus not feasible to apply this method for an extended model domain or for several points in time. Hence we limited the application of this method to the derivation of vertical profiles (Fig. 2) and a horizontal cross-section (Fig. 3b). We instead employed the dissipation method in Sect. 4.6 to investigate the variability of $C_{T}^2$ along horizontal paths in the lower boundary layer as well as for validation with local structure parameters from aircraft data.

Fig. 3

Cross-sections of $\mathrm{log_{10}}(C_{T}^2/C_{T,*}^2)$ in the surface layer at z $=$ 41 m (LAS height), derived from the dissipation (a) and wavelet methods (b). Results are shown for case M after 1 h of simulation time. Maximum and minimum values are given above the frames

Figure 4 shows the profiles of the variance $\sigma ^2$ of $C_{T}^2$ and $C_q^2$ (dissipation method). The shape of the profiles coincides with the structure-parameter profiles with a maximum located close to the surface and a secondary maximum at the top of the boundary layer (cf. Fig. 2). The surface peak is similar for cases M and A, whereas the upper maximum is more affected by different entrainment regimes as was pointed out in Sect. 4.2 (see also Moene et al. 2006). The variances rapidly decrease with height in the surface layer and slightly decrease above in the mixed layer until entrainment processes become important. For $C_q^2$ this difference is noticeable since humidity structures in the CBL are dominated by the entrainment of dry air from the free atmosphere. From Figs. 2 and 4 we can infer that $\mathrm{log_{10}}(\sigma ^2(C_{T}^2))$ and $\mathrm{log_{10}}(\sigma ^2(C_q^2))$ are linearly correlated to $\mathrm{log_{10}}(C_{T}^2)$ and $\mathrm{log_{10}}(C_q^2)$, respectively, even though the proportionality is not exact.

Fig. 4

Normalized profiles of the variances of $C_{T}^2$ (a) and $C_q^2$ (b) after 1 h from cases M and A, derived from the dissipation method

4.3.2 Comparison with Aircraft Data

By means of the wavelet method we calculated local structure parameters from the aircraft data (see Sect. 3.4.2). In order to compare the local $C_{T}^2$ and $C_q^2$ from aircraft with the LES data, a running average was applied to the local structure parameters from the dissipation method over a range of 208 m. This is identical to the upper limit of the spectral range over which the wavelet estimates were averaged. In Fig. 5 statistics of the aircraft measurements of the local $C_{T}^2,\,C_q^2$ and virtual measurements in the LES are shown at the three different flight levels.

Fig. 5

Statistics of $C_S^2$ along the aircraft flight legs (black, wavelet method) and virtual measurements along horizontal paths in the LES (grey, dissipation method) for case ME (a, b) and case AE (c, d) at three different heights. For the wavelet method, the spectral window 50-208 m was chosen. A running average over 208 m has been performed on the virtual paths in the LES to make them comparable to the aircraft data. The end of the whiskers represent the maximum/minimum values; the middle of the box is the average over all path-means, and the top and bottom of the boxes show one standard deviation of $\mathrm{log_{10}}(C_S^2/C_{S,*}^2)$ above and below this mean, respectively. The number of flights varied for each height and case between $3$ and $11$, whereas 1,024 virtual measurements were available from the LES data

From Fig. 5a, c it can be seen that the mean $C_{T}^2$ derived from the aircraft is greater than that from the LES data. This is consistent with the underrepresentation of small-scale variations in the LES, although the difference is not constant for different heights. This was already shown and discussed in Sect. 4.2.2 (cf. Fig. 2a, c). The variability of $C_{T}^2$ along the path is generally less for the aircraft data than for the LES. Since the spatial variability in the LES data is directly related to the length of the running average, the higher variability than observed for the aircraft data might be ascribed to the fact that the running average cannot exactly mimic the spatial averaging that is involved in the wavelet method procedure (see Sect. 3.4.1). The largest differences in the standard deviation are found at the lowest flight level, where large amplitude variations at small scales dominate. Here, averaging has a larger effect than at higher levels.

The spatial statistics for $C_q^2$ from LES are in remarkable agreement with the aircraft observations (see Fig. 5b,d). Both show a similar range of values as well as standard deviation at all flight levels and in both simulations. The mean values differ only slightly. In case ME the aircraft data provide higher spatial means than the LES-derived $C_q^2$, while in case AE the aircraft estimates tend to be lower. This is in agreement with the discussed mean profiles (see Fig. 2b, d).

4.4 Modelling $\varepsilon _S$ and $\varepsilon _\mathrm{TKE}$: Validation

In Sect. 4.2.1 we showed that the profiles of $C_S^2$, derived from the spectral and dissipation methods, differ in magnitude by a rather constant factor. We also showed that the shape of these profiles is very similar. However, one might claim that modelling the dissipation rates by means of Eqs. 10 and 11 is questionable. Cheinet and Siebesma (2009) compared their modelled dissipation profiles against the profiles from Sorbjan (1988) and found fairly good agreement. We now try to show that Eqs. 10–11 can be used for the derivation of $C_S^2$ by additionally calculating the dissipation rates directly from the turbulence spectra (Eqs. 5–7). The data processing was done analogous to the derivation of $C_S^2$ as described in Sect. 3.4.1.

Figure 6 shows the calculated profiles of $\varepsilon _{T},\,\varepsilon _q$, and $\varepsilon _\mathrm{TKE}$ for case M. It is obvious that the modelled profiles show the same shape as the profiles that have been derived from the spectra, but with a significant gap between them. The modelled profiles agree with the profiles shown by Cheinet and Siebesma (2009), while the dissipation rates from the spectral method are in much better agreement with Sorbjan (1988). While $\varepsilon _\mathrm{TKE}$ shows a slight linear decrease with height, the shape of the profiles of $\varepsilon _S$ is similar to that of $C_S^2$ (cf. Fig. 2a, b). As both methods (modelled and spectral) give profiles with the same shape, we can thus conclude that Eq. 10 and Eq. 11 are suitable for modelling the dissipation rates (at least for mean profiles). In Eq. 9 the underestimation in $\varepsilon _\mathrm{TKE}$ leads to an overestimation, but the underestimation in $\varepsilon _S$ dominates and yields an underestimation in $C_S^2$. The resulting profiles of $C_S^2$ from the spectral and dissipation methods hence differ by a constant factor. This gap between the two methods is explored below.

Fig. 6

Profiles of the modelled dissipation rate of temperature fluctuations (a), humidity fluctuations (b), and TKE (c) for case M (short dashed lines) and from the turbulence spectra (dashed lines). The profiles are on a logarithmic scale and have been normalized with $\varepsilon _{S,*} = \frac{S_*^2 w_*}{z_\mathrm{i}}$ (a, b) or $\varepsilon _{\mathrm{TKE},*} = \frac{w_*^3}{z_\mathrm{i}}$ (c). The profiles after Sorbjan (1988) are given by solid lines

4.5 Modelling $C_S^2$: Exploring the Gap Between the Spectral and Dissipation Methods

In the previous section we showed that a discrepancy between the modelled dissipation rates and those derived directly from the turbulence spectra lead to the gap in the vertical profiles of $C_S^2$. Cheinet and Siebesma (2009) supposed that the gap in $C_S^2$ might be ascribed to uncertainties in $\alpha ,\,\beta$, the low Prandtl number in their LES, and a decrease in the spectral density at the highest resolved wavenumbers. The latter will be the starting hypothesis for the analysis in this section.

Figure 7 shows the power spectral density of TKE, temperature and humidity ($\phi _\mathrm{TKE},\,\phi _{T}$ and $\phi _q$, respectively), where it is obvious that the spectra capture the inertial subrange very well. At high wavenumbers (small eddies), the power spectral density decreases significantly. This fall-off is a well-known effect of the SGS model, which dissipates energy at the smallest resolved scales (Moeng and Wyngaard 1988). For many higher-order advection schemes, such as WS-5, this fall-off is intensified by numerical dissipation (Glendening and Haack 2001). The spectral method derives $C_S^2$ directly from the power spectral density in the inertial subrange, while the dissipation method relates $C_S^2$ to the local gradients of $S$ (see Eq. 13). These gradients mainly capture small-scale variations of the turbulent flow and might thus be directly affected by the spectral fall-off at highest resolved wavenumbers. Furthermore, the discretization of the local gradients in space might play an important role as interpolation is necessary to determine the gradients at a specific location in the LES grid volume. In order to investigate these possible causes we replaced the central differences approximation of the gradients (see Sect. 3.4.1) with forward differences. We also carried out two comparative simulations with the PW-2 scheme, which does not suffer from numerical dissipation. Again, we present only the results of case M and restrict the analysis to $C_{T}^2$.

4.5.1 Effects of Interpolation

The scalar quantities are defined in PALM at the centre of the grid volumes, and in order to calculate the local gradients of temperature or humidity in all spatial directions at the same location, central finite differences are used. This is equivalent to calculating the local gradients using one-sided differencing and subsequent interpolation to the centre of the grid volume. Owing to the central differencing, scalar fluctuations at the scale of the LES grid $\varDelta _{x,y,z}$ are filtered out and cannot be captured. This approximation will consequently underestimate the turbulent fluctuations and hence also underestimate the structure parameters. For comparison we replaced the central differencing with simple forward differencing and omitted the interpolation to the same location. In this way the local gradients were calculated at different positions in the grid volume. This yields also incorrect local estimates of the structure parameters since the gradients implicit in Eq. 11 cannot be calculated at the same location. Although the local estimates will be slightly inaccurate, the horizontal average of the structure parameters, however, will be less affected by this inaccuracy (especially for the horizontal derivatives).

Fig. 7

Area-averaged spectra of TKE, temperature and humidity at a height of $z/z_\mathrm{i} = 0.5$, derived from case M with the fifth-order advection scheme of Wicker and Skamarock (2002) (solid lines) and second-order advection scheme of Piacsek and Williams (1970) (dashed lines)

Figure 8 (black lines) shows $C_{T}^2$, derived from the dissipation method using either central or forward differences, and in comparison with the spectral method. It is obvious that the gap between the spectral and dissipation methods is halved when using one-sided differences. This shows that at least 50 % of the gap might already be explained by the fact that the approximation of the gradient misses fluctuations at the scale of the LES grid spacing.

Fig. 8

Normalized profiles of $C_{T}^2$ from spectral (solid lines) and dissipation method after 1 h for case M, simulated with the advection schemes WS-5 and PW-2. For the dissipation method the temperature gradients have been approximated using central differencing (CD, dashed lines) and forward differencing (FD, short-dashed lines)

4.5.2 Effects of Numerical Dissipation of the Advection Scheme

Based on the finding from the previous section we carried out comparative simulations with the lower-order PW-2 advection scheme that does not suffer from numerical dissipation. The PW-2 scheme has some disadvantages, amongst which is that it suffers from immense numerical dispersion that leads to unrealistic small-scale structures. This advection scheme is thus not an appropriate choice for deriving realistic local estimates of the structure parameters.

Turbulence spectra from the simulations with PW-2 are additionally given in Fig. 7. A gap in the power spectral density is visible between simulations with PW-2 and WS-5 at the highest wavenumbers, caused by the additional numerical dissipation of the WS-5 scheme. This spectral fall-off leads to too little energy in the smallest resolved scales. It can also be seen that this effect is more prominent for TKE than for the scalar quantities. Furthermore, though less visible, the resolved energy level in the inertial subrange is slightly higher for WS-5 than for PW-2. Consequently, as shown in Fig. 8, $C_{T}^2$, derived from the spectral method, is slightly lower for PW-2 than for WS-5. $C_{T}^2$ derived from the dissipation method (central differences), however, does not show a significant response to a change in the advection scheme; at least up to heights where entrainment processes become important. This is counterintuitive as one would expect that the additional numerical dissipation should increase the destruction of fluctuations at the smallest resolved scales and hence decrease $C_{T}^2$.

4.5.3 Combined Effects of Interpolation and Numerical Dissipation

Figure 8 also shows the results for the combination of PW-2 with the one-sided approximation of the scalar gradients. This profile is in remarkable agreement with the respective profile from the spectral method for PW-2. Moreover, a small gap between PW-2 and WS-5 is shown that was not found for central differences. The additional dissipation thus seems to mainly influence the smallest scale, but does not significantly affect larger scales, which are captured by central differences as mentioned above. The good agreement between the spectral and dissipation methods for PW-2 is surprising, since we see from the turbulence spectra in Fig. 7 that the local gradient should suffer from the energy fall-off at high wavenumbers, even for PW-2. The reasons for this good agreement remain unclear and might possibly be ascribed to the fact that the local scalar gradients also carry information from smaller wavenumbers that are reasonably well resolved. Furthermore an overestimation of the signal due to the one-sided approximation is conceivable. However, we can assume that the remaining gap between the dissipation method (one-sided differences) and the spectral method with WS-5 is caused by the numerical dissipation of the advection scheme.

4.5.4 Summary

In summary we found that the observed gap between the spectral and dissipation methods can be traced back, to a great extent, to the numerical dissipation of the WS-5 advection scheme and the interpolation in space that was necessary to calculate the local scalar gradients. Since the gap between the spectral and dissipation methods is found to be a constant factor, and using one-sided differences give incorrect local estimates, we will use the most straightforward formulation, i.e. the dissipation method with centred differences and the more sophisticated WS-5 scheme for the rest of the article. This decision is also based on the fact that the spectral method does not allow the derivation of local estimates of the structure parameters and that the wavelet method was found to require enormous computational resources (see Sect. 4.3.1).

4.6 Application of LES Results to Estimate the Statistical Uncertainty in LAS Measurements

We now address one important source of errors in LAS measurements, the statistical uncertainty due to the temporal and spatial variability of $C_{T}^2$. Since $C_{T}^2$ depends on the randomly distributed turbulent fluctuations, the question arises whether the path-averaged $C_{T}^2$ is representative for the horizontal mean under horizontal homogeneous surface conditions. Since LES allows for deriving $C_{T}^2$ as a four-dimensional quantity, it presents itself as a unique instrument with which to study the variability of LAS path measurements.

4.6.1 Spatial Variability of $C_{T}^2$ Along a Virtual LAS Path

Figure 9 shows the variability of $C_{T}^2$ along an arbitrarily chosen virtual path for cases ME and AE at a height of 41 m (height of the LAS at Cabauw). The probability density functions of the shown spatial series suggest a log-normal distribution of $C_{T}^2$ along the path, a distribution that can be classified into two different turbulence regimes. Low turbulence intensity with low $C_{T}^2$ outside the plumes alternates with high turbulence regions and high $C_{T}^2$ values inside the plumes. The probability density functions support the two-regime model, which suggests a superposition of two log-normal distributed convective regimes (light background turbulence and strong turbulence within plumes). Petenko and Shurygin (1999) introduced this two-regime concept based on sodar measurements and it was also found in the LES data of Cheinet and Siebesma (2009). Local maxima occur frequently at the edges of plumes, where the largest gradients in temperature reside (cf. Fig. 3). Case ME exhibits less variance in the scaled and logarithmic $C_{T}^2$ along the path $(\sigma ^2 = 1.12)$ than case AE $(\sigma ^2 = 1.43)$. The VLAS measurement in case ME gives $\mathrm{log_{10}}(\langle \widetilde{C_{T}^2} \rangle _\mathrm{p}/C_{T,*}^2) = 1.4,$ which is lower than in case AE $(\mathrm{log_{10}}(\langle \widetilde{C_{T}^2} \rangle _\mathrm{p}/C_{T,*}^2) = 2.0)$.

These findings are closely related to the normalized height of the VLAS and the stability parameter $-z/L$, with

$$\begin{aligned} L = \frac{- \langle \theta _\mathrm{v}\rangle \langle u_* \rangle ^3}{\kappa \ g\ \overline{w^{\prime }\theta _\mathrm{v}^{\prime }}_0} \end{aligned}$$

(18)

being the Obukhov length, where $\theta _\mathrm{v}$ is the virtual potential temperature and $\kappa = 0.4$ is the von Kármán constant. Since $u_*$ is calculated locally in the LES (see Sect. 3.3), the horizontal average deviates from zero, even in the local free convection limit. In the surface layer, which we simply assume to be the lowest 10 % of the boundary layer $(z/z_\mathrm{i} \le 0.1)$, there is greater variance than in the mixed layer above (see Fig. 4). Since the nominal height of the VLAS is constant, it is evident that in the shallow CBL, which develops in the morning, the normalized height of the VLAS is $z/z_\mathrm{i} \approx 0.1$. The VLAS is thus located at the top of the surface layer. Braam et al. (2012) showed that the LAS at Cabauw can be above the surface layer frequently in the early morning hours. In the afternoon $z_\mathrm{i}$ increases in such a way that the VLAS is well within the surface layer (here $z/z_\mathrm{i} = 0.04$). At the same time $-z/L$ increases, leading to more unstable conditions at the VLAS height. It is not possible to separate both effects. The virtual measurement $\langle \widetilde{C_{T}^2} \rangle _\mathrm{p}$ and the variance along the path, however, are consequently higher in the afternoon than in the morning.

Fig. 9

$C_{T}^2$ along an arbitrarily chosen VLAS path of 9.8 km length at a height of 41 m for case ME (top left) and case AE (middle left) after 1 h simulation time. Red colours refer to updrafts (vertical velocity $w > 0.3\,{\mathrm{m s}^{-1}}$), blue colours for background turbulence $(w \le 0.3\,{\mathrm{m s}^{-1}})$. The normalized VLAS measurements $(\mathrm{log}_{10}(\langle \widetilde{C_{T}^2} \rangle _\mathrm{p}/C_{T,*}^2)$ and the variance of $\mathrm{log}_{10}(C_{T}^2/C_{T,*}^2)$ are listed in the graphs. The probability density functions of updraft regions, background turbulence and the sum of both (black) of the shown spatial series of $\mathrm{log_{10}}(C_{T}^2/C_{T,*}^2)$ are given on the right side. The bottom graph displays the path-weighting function (PWF) along the path for the VLAS measurements

4.6.2 Temporal Variability of the Path-Averaged $C_{T}^2$

The temporal variability of a single VLAS measurement at 41 m for a path length of 9.8 km is shown in Fig. 10, along with the temporal mean over the analysis period of 1 h. The path mean of $C_{T}^2$ varies rapidly in time, due to the turbulent motions along the path. These fluctuations result in relative standard deviations (defined as the standard deviation divided by the mean; RSD) of about 11 %. We found values around 11 % to be representative for all VLAS in the LES, but to be strongly dependent on the path length. This result is in agreement with the LAS data that showed an RSD between 13 and 15 % during the measurement period (not shown). For a shorter path in the LES of only 2 km, RSD increases up to 22 %. A temporal average over an appropriate period (see below) is thus required in order to ensure a low statistical uncertainty. Furthermore, $\langle \widetilde{C_{T}^2} \rangle _\mathrm{p}$ (and $\langle C_{T}^2 \rangle _\mathrm{p}$ in the mixed layer), on-the one hand, was found to decrease with height, while on the other hand, its RSD increased with height. This is in agreement with Cheinet and Siebesma (2007).

Fig. 10

Time series of the normalized $\langle \widetilde{C_{T}^2} \rangle _\mathrm{p}$ from the VLAS (path length of 9.8 km) at a height of 41 m for case AE (top) and case ME (bottom). The time averages $\langle \overline{\widetilde{C_{T}^2}} \rangle _\mathrm{p}$ of the LES series are plotted as grey lines

4.6.3 Representativeness of the Path Average

From the previous Sect. 4.6.1 and Sect. 4.6.2 it is evident that the spatial variability of $C_{T}^2$ along the VLAS path, as well as the temporal variability of the path mean, can lead to significant fluctuations in $C_{T}^2$ and thus to variations in the VLAS measurements $\langle \widetilde{C_{T}^2} \rangle _\mathrm{p}$. In order to evaluate the statistical uncertainty of a single virtual measurement due to insufficient temporal/spatial averaging of the randomly distributed convective motions, we determined the RSD of $C_{T}^2$ from the available virtual path measurements (at least 1,024, depending on the path length). By calculating the RSD, it is possible to estimate the representativeness of path measurements of $C_{T}^2$ for a homogeneous area, i.e. the model domain.

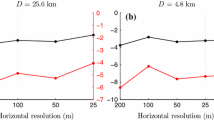
The uncertainty in LAS measurements can be reduced by adding temporal averaging to the path averaging. We thus calculated RSD as a function of the VLAS path length and the temporal averaging period at different height levels (every 4 m). The maximum path length was restricted by the model domain size. The longer the path distance, the more convective updrafts and downdrafts can be captured and consequently averaged by a single path measurement. Since the VLAS measurements during daytime are usually within the surface layer, the ground might have more influence on the turbulence than the capping inversion and $z_\mathrm{i}$ should not be a relevant parameter (Wyngaard et al. 1971a). Hence, local free convection scaling was applied. For in situ measurements $z_\mathrm{i}$ and the surface fluxes might change rapidly. Time-averaging intervals of 1 h are thus usually not exceeded, and we limit ourselves to practically relevant cases and limit the temporal average to at most 1 h.

We found RSD to depend on the height of the VLAS, and in order to achieve results that are valid for any LAS set-up in the local free convection layer, we scaled the path length with its height above the ground. The results showed that RSD now mainly depended on the ratio of the VLAS path length to height above the ground, at least for VLAS measurements at $z/z_\mathrm{i} \le 0.1$ (we analyzed data every 4 m in the $z$-direction). Here RSD differed only by 2–3 % between different heights. Figure 11 shows that RSD decreases with increasing averaging time and path length. For a VLAS of 9.8 -km length at a height of 41 m (equivalent to a ratio of $239$), RSD is about 15 % in both cases, if no time average is applied. Additional averaging over a period of 15 min (case ME) and 10 min (case AE) is able to reduce RSD to below 10 %, which we regard as a target value below. For shorter VLAS paths (lower ratio of length to height), a longer averaging period is necessary to obtain the same RSD values. Figure 11 shows that the path in any case requires a length of at least $80z$ in order to obtain $RSD \le 10$ %. This also supports the result of Cheinet and Siebesma (2007) that a measurement height of 80 m and a path distance of 2 km (equivalent to $25z$) is not sufficient to obtain representative path-averaged values. Unfortunately we did not find a suitable time scale to make the temporal-averaging interval dimensionless so that Fig. 11a, b become more similar. We tried to apply the surface-layer time scale (free convection, see Stull 1988 as well as the convective time scale $(z_\mathrm{i}/w_*)$, but the results suggested that a suitable scale would be somewhere in between, at least for the two studied cases. Anyhow, Fig. 11 suggests a rough independence of our results from the boundary-layer depth, and might be used to estimate the statistical uncertainty for a given LAS system in the surface layer. We are aware of the fact that this conclusion is based on the results from only two different simulations and that a more detailed sensitivity study would be required to evaluate whether our findings are case-sensitive or if they are valid for an arbitrary LAS set-up.

From these findings we return to the uncertainties of the measurements at Cabauw. Table 4 shows RSD for both LAS and aircraft, derived from the VLAS and virtual aircraft measurements of the structure parameters. The VLAS data were averaged over a time interval of 10 min, which was the same averaging interval that was applied to the LAS data. The aircraft measured instantaneously over a path length of about 10 km. The RSD for the LAS at Cabauw is below 10 %, owing to the extremely long LAS path with a combined time average. In contrast to the LAS, no explicit time averaging was feasible for aircraft data. Table 4 suggests that a higher RSD up to 23 % has to be considered for a single flight. When more repetitions are flown, RSD will decrease (four repetitions would reduce RSD by a factor of 2). Our analysis suggests that a typical uncertainty in the order of 10–20 % has to be taken into account. It is also shown that RSD increases with height in the lower half of the mixed layer as suggested by Cheinet and Siebesma (2007).

Fig. 11

RSD of $\langle \overline{\widetilde{C_{T}^2}} \rangle _\mathrm{p}$ (in %) against the time-averaging interval and the ratio of path length to the path height (here 41 m above ground)

Table 4 RSD (in %) of $\langle \overline{C_{T}^2}\rangle _\mathrm{p}$ (flights) and $\langle \overline{\widetilde{C_{T}^2}} \rangle _\mathrm{p}$ (LAS) at different heights for the Cabauw measurements derived from LES

5 Summary and Conclusions

The turbulent structure parameters for temperature and humidity were investigated by means of LES of the CBL. Two high-resolution simulations of the morning and afternoon CBL, driven by airborne and surface measurements at Cabauw in The Netherlands, were performed. Three different methods, based on the Fourier spectrum of turbulence, a method based on local dissipation rates and a new method based on the local estimate of the Fourier spectrum using wavelet analysis were used to obtain vertical profiles of the structure parameters from LES data. We found that the methods based on the power spectral density in the inertial subrange from Fourier spectra and wavelet analysis compare very well with the proposed profiles after Kaimal et al. (1976) and Fairall (1987). The derivation of local estimates of the structure parameters by means of the method based on wavelets, however, turned out to be rather problematic as it required enormous computing time. Moreover we derived $C_{T}^2$ and $C_q^2$ from aircraft oberservations and LAS measurements at Cabauw, and found that LES estimates of $C_{T}^2$ were in very good agreement with the LAS observations. The LES data did compare well for $C_q^2$ with the aircraft observations, but $C_{T}^2$ from the aircraft data did not show the proposed decrease with height, for which we do not have a satisfying explanation. It can possibly be ascribed to wind shear or variance production by a mesoscale gradient in advected scalar fields (Kimmel et al. 2002), which was not considered in the LES.

Local structure parameters were derived by means of a method based on local dissipation from the LES data. The characteristics of these local structure parameters were in agreement with the recent LES of Cheinet and Siebesma (2009) and Cheinet and Cumin (2011) and reflect the structure of turbulence well. This was shown by means of probability density functions that supported the two-regime model developed by Petenko and Shurygin (1999) based on sodar measurements. Moreover, both dissipation and wavelet methods displayed the same cellular pattern of high intensity and low intensity turbulence in the surface layer. However, a gap in the magnitude between the structure parameters from the spectral and dissipation methods was observed. It can be ascribed to a combined effect of the approximation of the local gradients of temperature and humidity by means of central differencing and additional numerical dissipation of the fifth-order scheme after Wicker and Skamarock (2002). We could show that central differencing implies an underestimation in the local scalar gradients that makes up 50 % of the observed gap in the structure parameters. A comparison of the vertical profiles from simulations with the fifth-order advection scheme and a second-order scheme of Piacsek and Williams (1970), which does not suffer from numerical dissipation, showed that the remaining underestimation of the structure parameter vanished in the absence of numerical dissipation.

Horizontal virtual path measurements of $C_{T}^2$ at different heights were used in order to explore the spatial and temporal variability along a single line or LAS path. The representativeness of path measurements for a horizontal area was studied using the statistical uncertainty due to the randomly distributed convection. We focussed on the implications for LAS in the surface layer and airborne measurements. We found that fluctuations of $C_{T}^2$ in time and space along a given path lead to a high variability of the path-averaged virtual measurements, which can affect LAS and aircraft observations. This estimated uncertainty increased with height up to the middle of the mixed layer.

The statistical uncertainty that results from this variability was found to strongly depend on the path length, the height above the ground and the temporal averaging interval. For the LAS that is installed at Cabauw at a height of 41 m above the ground (Kohsiek et al. 2002) it is found that the path length of 9.8 km is sufficient to obtain representative measurements for the fairly homogeneous area with a statistical uncertainty $\le 10\,{\%}$. For other LAS, which cover a shorter path (e.g. at Lindenberg, Germany, see Meijninger et al. 2006), a longer time-averaging interval might be required to reduce the statistical uncertainty down to 10 %. The required spatial averaging in the surface layer was found to depend on the ratio of path length to height above the ground. For LAS this ratio is a constant and the time averaging must thus be chosen in an appropriate way. Our results point out that, for a daytime CBL, an averaging interval of up to 1 h might be necessary for LAS measurements, depending on the LAS beam height and path length. Such long averaging intervals are strictly limited to changes in the surface fluxes and the diurnal cycle. Consequently, a higher statistical uncertainty has to be considered, if sufficient averaging is not possible.

In order to derive the surface sensible heat flux from $C_{T}^2$ and Monin–Obukhov similarity theory, the height of the LAS must be within the surface layer. It is evident that for a shallow CBL (e.g. in the early morning), the LAS might not be within the surface layer. For aircraft measurements, where a temporal averaging is not feasible, we found that the statistical uncertainty is higher than for LAS and can reach the order of 25 % for a path length of 10 km, depending on the height above the ground.

In a follow-up study we will further address the uncertainty of the flux estimates by the LAS and aircraft measurements in the idealized homogeneously-heated CBL, but especially under more realistic heterogeneous conditions.

Appendix

1.1 Path-weighting function

For the virtual LAS measurements, we used the path-weighting function $W$ after Wang et al. (1978) in the formulation of Hartogensis et al. (2003):

$$\begin{aligned} W(u) = 16 \pi k_\mathrm{LAS}^2 L_\mathrm{LAS} \int \limits _0^{\infty } k \varPhi _n(k) \sin ^2\left[ \frac{k^2L_{\mathrm{LAS}}u(1-u)}{2k_\mathrm{LAS}} \right] \left[ \frac{2 J_1(x_1) 2 J_1(x_2)}{x_1x_2}\right]^2 dk, \end{aligned}$$

(19)

where $u = x / L_{\mathrm{LAS}}$ is the dimensionless position along the path of length $L_\mathrm{LAS},\,k_\mathrm{LAS} = 2 \pi / \lambda$ is the optical wavenumber of the emitted signal ($\lambda = 940\,{\mathrm{nm}}$ for the LAS at Cabauw), and $\varPhi _n(k) = 0.033k^{-11/3}$ is the three-dimensional spectrum of the refractive index in the inertial subrange. $J_1$ is the Bessel function of the first kind, $x_1 = kDu/2$ and $x_2 = [kD (1-u)]/2$, where $D$ is the aperture diameter of the scintillometer ($D = 0.31\,{\mathrm{m}}$ for the LAS at Cabauw). Hartogensis et al. (2003) showed that the path-averaged structure parameter $C_{T}^2$ can be derived from the local $C_{T}^2$ by

$$\begin{aligned} \langle \widetilde{C_{T}^2} \rangle _\mathrm{p} = \int \limits _0^1 C_{T}^2(u)G(u)du, \end{aligned}$$

(20)

where

$$\begin{aligned} G(u) = \frac{W(u)}{\int _0^1 W(u) du}. \end{aligned}$$

(21)