Period doubling bifurcation problems in the softening Duffing oscillator with nonstationary excitation

Abstract

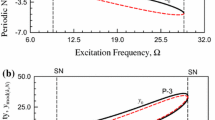
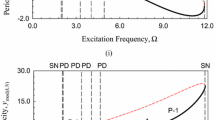
The Duffing oscillators are widely used to mathematically model a variety of engineering and physical systems. A computational analysis has been initiated to explore the effects of nonstationary excitations on the response of the softening Duffing oscillator in the region of the parameter space where the period doubling sequences occur. Significant differences between the stationary and nonstationary responses have been uncovered: (i) the stationary transitions from T to 2T, from 2T to 4T ... etc. branches at the stationary period doubling bifurcations are smooth, in nonstationary cases they exhibit jumps to the near stationary branches at the values of the control parameters greater than those for the stationary; this phenomenon is called penetration (delay or memory). The lengths of the penetrations is being compressed to zero with the increasing number of the iterations. (ii) The stationary and nonstationary responses eventually settle on different limit motions, the nonstationary has modulated components. (iii) The jumps appearing in the stationary bifurcation diagram at 2T from the upper to the lower branches of the (x, f) and (x, Ω), i.e., (displacement-forcing amplitude) and (displacement-forcing frequency), diagrams have been replaced by continuous transition in the nonstationary diagram climinating thus the discontinuity. Apart from these differences, some specific characteristic nonstationary responses have been observed not encountered in the stationary cases: (iv) the appearance of the ‘window’ in the nonstationary limit bifurcation diagrams. (v) The nonstationary limit motions located on the upper (lower) branches of the (x, f) or (x, Ω) diagrams expanded rapidly to the lower (upper) branches. (vi) The stationary and nonstationary bifurcation diagrams are extremely sensitive to the initial conditions, manifested by the mirror reflections, called the flipflop phenomenon. (vii) The nonstationary limit motion has been characterized by a complex phase portrait, the appearance of the Cantor-like set of the limit motion bifurcation plot, and continuous spectral density. For the purpose of comparison, a stationary period doubling sequence T, 2T,..., 2ⁿ T,... stationary limit motion, _χST which is known to be chaotic has been determined. A far reaching observation has been made in the process of this study: the determination of the nonstationary bifurcations, their branches and limit motions, has been independent of the calculations of the stationary ones, indicating, thus, the existence of an independent class of nonstationary (time varying) dynamics.