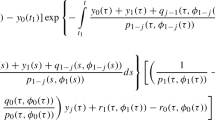Abstract
A single-mass two-degrees-of-freedom system is considered, witha radially oriented nonlinear restoring force. The latter is smooth andbecomes infinite at a certain value of a radial displacement. Stabilityanalysis is made for planar oscillation, or motion along a givendirection. As long as this motion is periodic, the nonlinearity in therestoring force provides a periodic parametric excitation in thetransverse direction. The linearized stability analysis is reduced tostudy of the Mathieu equation for the (infinitesimal) motions in thetransverse direction. For the case of free oscillations in the givendirection an exact solution is obtained, since a specific analyticalform is used for the (strongly nonlinear) restoring force, which permitsexplicit integration of the equation of motion. Stability of the planarmotion in this case is shown to be very sensitive to even slightdeviations from polar symmetry in the restoring force (as well as to theamplitude of oscillations in the given direction). Numerical integrationof the original equations of motion shows the resulting motion to be awhirling type indeed in case of the transversal instability. For thecase of a sinusoidal forcing in the given direction solution for the(periodic) response is obtained by Krylov–Bogoliubov averaging. Thisresults in the ‘transmitted’ Ince–Strutt chart – namely, stabilitychart for transverse direction on the amplitude-frequency plane of theexcitation in the original direction.
Similar content being viewed by others
References
Rega, G., Alaggio, R., and Benedettini, F., ‘Experimental investigation of the nonlinear response of a hanging cable. Part 1: Local analysis’, Nonlinear Dynamics 14, 1997, 89–117.
O'Reilly, O. and Holmes, P.J., ‘Nonlinear, non-planar and non-periodic vibrations of a string’, Journal of Sound and Vibration 153, 1992, 413–435.
Rubin, M. B. and Gottlieb, O., ‘Numerical solutions of forced vibration and whirling of a non-linear string using the theory of Cosserat point’, Journal of Sound and Vibration 197(1), 1996, 85–101.
Tondl, A., Quenching of Self-Excited Vibrations, Academia, Prague, 1991.
Svoboda, R., Tondl, A., and Verhulst, F., ‘Autoparametric resonance by coupling of linear and non-linear systems’, International Journal of Non-Linear Mechanics, 29, 1994, 225–232.
Manevich, L. I., Mikhlin, Ju. V., and Pilipchuk, V. N., Method of Normal Vibrations for Essentially Nonlinear Systems, Nauka, Moscow, 1989 [in Russian].
Nesterov S. V. 'Examples of nonlinear Klein-Gordon equations, solvable in terms of elementary functions’, Proceedings of the Moscow Institute of Power Engineering 357, 1978, 68–70, [in Russian].
Abramowitz, M. and Stegun, I. A., Handbook of Mathematical Functions, Dover, New York, 1972.
Nayfeh, A. H. and Mook, D. T., Nonlinear Oscillations, Wiley, New York, 1979.
Gradshtein, I. S. and Ryzhik, I. M. Tables of Integrals, Series and Products, 1980.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Dimentberg, M.F., Iourtchenko, D.V. & Bratus', A.S. Transition from Planar to Whirling Oscillations in a Certain Nonlinear System. Nonlinear Dynamics 23, 165–174 (2000). https://doi.org/10.1023/A:1008369303110
Issue Date:
DOI: https://doi.org/10.1023/A:1008369303110