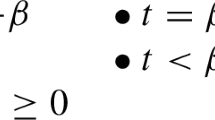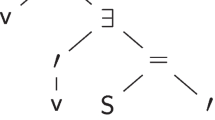Abstract
The need to reason with imprecise probabilities arises in a wealth of situations ranging from pooling of knowledge from multiple experts to abstraction-based probabilistic planning. Researchers have typically represented imprecise probabilities using intervals and have developed a wide array of different techniques to suit their particular requirements. In this paper we provide an analysis of some of the central issues in representing and reasoning with interval probabilities. At the focus of our analysis is the probability cross-product operator and its interval generalization, the cc-operator. We perform an extensive study of these operators relative to manipulation of sets of probability distributions. This study provides insight into the sources of the strengths and weaknesses of various approaches to handling probability intervals. We demonstrate the application of our results to the problems of inference in interval Bayesian networks and projection and evaluation of abstract probabilistic plans.
Similar content being viewed by others
References
C. Boutilier and R. Dearden, Using abstractions for decision-theoretic planning with time constraints, in: Proceedings of the 12th National Conference on Artificial Intelligence, Seattle (July 1994) pp. 1016–1022.
L. Chrisman, Abstract probabilistic modeling of action, in: Proceedings of the 1st International Conference on Artificial Intelligence Planning Systems (June 1992) pp. 28–36.
L. Chrisman, Incremental conditioning of lower and upper probabilities, Internat. J. Approximate Reason. 13(1) (1995) 1–25.
F. Cozman, Robustness analysis of bayesian networks with local convex sets of distributions, in: Proceedings of the 13th Conference on Uncertainty in Artificial Intelligence (August 1997) pp. 108–115.
T. Dean, L. Pack Kaelbling, J. Kirman and A. Nicholson, Planning under time constraints in stochastic domains, Artif. Intell. 76(1–2) (1995) 35–74.
R. Dechter, Bucket elimination: A unifying framework for probabilistic inference algorithms, in: Proceedings of the 12th Conference on Uncertainty in Artificial Intelligence (August 1996) pp. 211–219.
A. Dempster, Upper and lower probabilities induced by a multi-valued mapping, Ann. Math. Statist. 38(2) (1967) 325–339.
D. Draper, Localized partial evaluation of Bayesian belief networks, Ph.D. thesis, Computer Science Department University of Washington, Seattle (November 1995).
R. Fagin and J. Halpern, A new approach to updating belief, in: Uncertainty in Artificial Intelligence, Vol. 6, eds. P. Bonissone, M. Henrion, L. Kanal and J. Lemmer (1991) pp. 347–374.
K.W. Fertig and J.S. Breese, Probability intervals over influence diagrams, IEEE Transactions on Pattern Analysis and Machine Intelligence 15(3) (1993) 280–286.
B. Grunbaum, Convex Polytopes (Interscience, London/New York, 1967).
V. Ha and P. Haddawy, Theoretical foundations for abstraction-based probabilistic planning, in: Proceedings of the 12th Conference on Uncertainty in Artificial Intelligence, Portland (August 1996) pp. 291–298.
P. Haddawy, A. Doan and C.E. Kahn Jr., Decision-theoretic refinement planning in medical decision making: Management of acute deep venous thrombosis, Medical Decision Making 16(4) (1996) 315–325.
S. Hanks, Practical temporal projection, in: Proceedings of the 18th National Conference on Artificial Intelligence, Boston (July 1990) pp. 158–163.
J. Jaffray, Bayesian updating and belief functions, IEEE Transactions on Systems, Man, and Cybernetics 22(5) (1992) 1144–1152.
H. Kyburg Jr., Bayesian and non-bayesian evidential updating, Artif. Intell. 31(3) (1987) 271–294.
H. Kyburg and M. Pittarelli, Set-based bayesianism, IEEE Transactions on Systems, Man, and Cybernetics 26 (1996) 324–339.
I. Levi, The Enterprise of Knowledge (MIT Press, Cambridge, MA, 1980).
T. Seidenfeld, M. Schervish and J.B. Kadane, On the shared preferences of two bayesian decision makers, J. Philosophy 86 (1989) 225–244.
G. Shafer, A Mathematical Theory of Evidence (Princeton University Press, Princeton, NJ, 1976).
P. Snow, Bayesian inference without point estimates, in: Proceedings of the National Conference on Artificial Intelligence (AAAI) (1986) pp. 233–237.
P. Snow, Improved posteriori probability estimates from prior and conditional linear constraint systems, IEEE Transactions on Systems, Man, and Cybernetics 21(2) (1991) 464–469.
W. Stirling and A. Morrell, Convex bayesian decision theory, IEEE Transactions on Systems, Man, and Cybernetics 21(1) (1991) 173–183.
V. Strassen, Messfehler and information, Z. fur Wahrscheinlichkeits-theorie und Verw. Gebiete 2 (1964) 273–305.
B. Tessem, Interval probability propagation, Internat. J. Approx. Reason. 7 (1992) 95–120.
S. Thiebaux, J. Hertzberg, W. Shoaff and M. Schneider, A stochastic model of actions and plans for anytime planning under uncertainty, Internat. J. Intell. Syst. (1994).
P. Walley, Statistical Inference with Imprecise Probabilities (Chapman and Hall, London, 1991).
C. White, A posteriori representations based on linear inequality descriptions of a priori and conditional probabilities, IEEE Transactions on Systems, Man, and Cybernetics 16 (1986) 570–573.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Ha, V.A., Doan, A., Vu, V.H. et al. Geometric foundations for interval-based probabilities. Annals of Mathematics and Artificial Intelligence 24, 1–21 (1998). https://doi.org/10.1023/A:1018936829318
Issue Date:
DOI: https://doi.org/10.1023/A:1018936829318