1 Introduction

Fluid inclusions (FIs) recorded the chemical compositions of paleo-geofluids and could provide important information for the relevant physicochemical conditions (e.g., temperature, pressure, pH, Eh) of geological processes (e.g., Roedder and Bodnar 1980; Bergman and Dubessy 1984; Roedder 1984; Petrychenko et al. 2005). In the field of petroleum geology, in combination with the construction of burial history, microthermometric analyses of FIs hosted in authigenic reservoir cements have been applied to investigate the hydrocarbon accumulation process, including the timing and the temperature–pressure (T–P) conditions (e.g., Burruss et al. 1983; Bodnar 1990; Thiéry et al. 2000; Munz 2001; Cao et al. 2006; Guo et al. 2012; Cui et al. 2013; Li et al. 2015; Chen et al. 2016; Fang et al. 2017). Methane (CH4) and carbon dioxide (CO2) are common components in the vapor phase of hydrocarbon-bearing FIs trapped under elevated T–P conditions (e.g., Pironon et al. 2001; Dutkiewicz et al. 2003; Lüders et al. 2012). Then trying to fathom the composition of the CH4–CO2 mixture is required for the measurements of the fluid composition, which is also essential for revealing fluid-trapping T–P conditions.

Conventionally, the composition of a FI can be obtained through microthermometric measurements (e.g., Collins 1979; Roedder 1984; Darling 1991; Bodnar 1993). However, this method is difficult to be applied to small FIs with diameter of < 5 µm, and the complex composition of geofluids cannot be accurately measured based on phase diagrams of simple fluid systems (Hollister and Crawford 1981; Mernagh and Wilde 1989; Chou et al. 1990; Walter et al. 2017). Alternatively, in situ Raman spectroscopy can provide quantitative information of FIs based on systemic experimental calibrations (e.g., Pasteris et al. 1988; Mernagh and Wilde 1989; Chou et al. 1990; Lu et al. 2007; Wang et al. 2011). This method is fast and nondestructive, and the spatial resolution of a microscopic confocal Raman spectrometer can reach 2–3 µm.

The intensity of a Raman active species, i, is a function of many factors (see Schmidt 2009). Wopenka and Pasteris (1986) simplified the expression of the Raman intensity of species i as:

$$A_{i} = C_{i} \times \eta_{i} \times \sigma_{i} \times I_{\text{L}}$$
(1)

where A is the integrated Raman intensity (i.e., peak area), C is the number of Raman active molecules in the analyzed volume, η is the instrument efficiency factor, σ is the Raman scattering coefficient, and IL is the intensity of incident light. For two Raman active components, a and b, in a homogeneous gas phase, their molar ratios can be calculated based on their Raman peak area ratios (Wopenka and Pasteris 1987; Pasteris et al. 1988; Chou et al. 1990):

$${{A_{\text{a}} } \mathord{\left/ {\vphantom {{A_{\text{a}} } {A_{\text{b}} }}} \right. \kern-0pt} {A_{\text{b}} }} = {{(C_{\text{a}} } \mathord{\left/ {\vphantom {{(C_{\text{a}} } {C_{\text{b}} )}}} \right. \kern-0pt} {C_{\text{b}} )}} \times ({{\eta_{\text{a}} } \mathord{\left/ {\vphantom {{\eta_{\text{a}} } {\eta_{\text{b}} }}} \right. \kern-0pt} {\eta_{\text{b}} }}) \times {{(\sigma_{\text{a}} } \mathord{\left/ {\vphantom {{(\sigma_{\text{a}} } {\sigma_{\text{b}} }}} \right. \kern-0pt} {\sigma_{\text{b}} }}) = ({{C_{\text{a}} } \mathord{\left/ {\vphantom {{C_{\text{a}} } {C_{\text{b}} }}} \right. \kern-0pt} {C_{\text{b}} }}) \times ({{F_{\text{a}} } \mathord{\left/ {\vphantom {{F_{\text{a}} } {F_{\text{b}} }}} \right. \kern-0pt} {F_{\text{b}} }})$$
(2)

where Fa/Fb is the Raman quantification factor of a relative to b. In general, the reported Raman quantification factors of gaseous i are relative to N2. For example, FCH4 is the Raman quantification factor of CH4 relative to N2. Theoretically, if the Raman quantification factors of CH4 and CO2 are known, we can measure the molar ratios between CH4 and CO2 in CH4–CO2 mixtures through Raman spectroscopic analyses. However, the reported FCH4 and FCO2 are quite different among different laboratories (Wopenka and Pasteris 1987; Seitz et al. 1993, 1996; Xi et al. 2014), and the effect of fluid pressure still needs further investigation (c.f., Chou et al. 1990; Seitz et al. 1993, 1996). In pure CH4 system, the symmetric stretching vibration band of CH4 (v1) shifts to lower wavenumber with rising pressure at constant temperature (Lin et al. 2007; Lu et al. 2007; Shang et al. 2015). Therefore, the wavenumber of v1(CH4) band can be used to calculate the pressure of CH4. In fact, the v1(CH4)-P curve can also be applied to CH4-dominated dry gas. For example, the experimental works of Seitz et al. (1993, 1996) demonstrated that the presence of minor amount of CO2 or N2 does not change the v1(CH4)-P curve significantly. Because the reported v1(CH4)-P curves are quite different, Lu et al. (2007) constructed a “unified” v1(CH4)-P curve for calculation of the CH4 pressure. This method needs an accurate determination of the v1(CH4) wavenumber of low-pressure CH4 (e.g., < 1 bar). Considering the experimental conditions which are different among different laboratories, a more practical method is to construct the laboratory-based v1(CH4)-P calibration curve.

In this study, we used fused silica capillary tubing as spectroscopic cell (Chou et al. 2005; Wang et al. 2011). CH4 and CH4–CO2–CO–N2 mixtures with known composition were loaded into the silica tubing and pressurized to pressures up to 136 MPa. In situ Raman spectra of these gases were collected at room temperature (22 °C). The Raman quantification factors, FCH4 and FCO2, were determined, and the v1(CH4)-P curve was constructed. Then, we analyzed the gas composition and pressure of two-phase aqueous and single-phase gas FIs hosted in quartz veins in the Lower Silurian Longmaxi Formation shale in Sichuan Basin. Compared with the available burial history, a paleo-overpressure of CH4-saturated fluid was proposed.

2 Experimental methods

2.1 High-pressure optical cell

The procedures for preparing a high-pressure optical cell (HPOC) were presented in Chou et al. (2005) and Wang et al. (2011). Pure CH4 (99.99% purity) and CH4–CO2–CO–N2 mixture with molar ratio of 1:1:1:2 were purchased from Jiahe Air Chemical (Shanghai) Co. Ltd. CH4 or CH4–CO2–CO–N2 gas was loaded into the cell and then was sealed using mercury at room temperature (Fig. 1; Wan et al. 2017). In this study, water was used as pressure medium. The pressure inside the line and cell was adjusted by a pressure generator. Pressures were measured by an Omega PX91N0-35KSV digital pressure transducer with Omega DP41-S-230 manometer (241 MPa full scale, accurate to ± 0.5%). The experimental setup is shown in Fig. 1. In order to maintain the sample temperature at 22 °C, the HPOC was inserted into a Linkam CAP500 heating–cooling stage (Wan et al. 2015).

Fig. 1
figure 1

A schematic diagram showing the experimental setup

Full size image

2.2 Raman spectroscopic analyses and spectral processing

In situ Raman spectra of pure CH4 and CH4–CO2–CO–N2 mixture were collected using a high-resolution JY/Horiba Raman spectrometer (LabRaman HR 800). The wavelength of the air-cooled frequency-doubled Nd:YAG excitation laser is 532 nm. A 50 × Olympus long-working distance objective and an 1800 groove/mm grating with spectral resolution of approximately 1 cm−1 were applied. The spectrometer was calibrated with the 520.7 cm−1 peak of silicon. For the pure CH4 system, the Ne emission lines at 2835.22 and 3006.36 cm−1 were also collected simultaneously (Fig. 2). Then, the v1(CH4) peak position was calibrated following the procedures presented in Kim et al. (1986) and Fang et al. (2018).

Fig. 2
figure 2

Typical spectra of pure CH4 (upper) and CH4–CO2–CO–N2 mixture (lower). Note that the neon emission lines at 2835.22 and 3006.36 cm−1 are collected simultaneously to calibrate the v1(CH4) peak position for pure CH4. For the CH4–CO2–CO–N2 mixture, the spectra of diamond at ~ 1331.70 cm−1 (star) are also collected to calibrate the spectrometer. Gray areas in the lower spectrum showing the ranges of wavenumber for the calculation of the relevant peak areas

Full size image

For the CH4–CO2–CO–N2 system, the peak areas of v1(CH4) band (ACH4), the upper band of v1–2v2(CO2) (ACO2), and v1(N2) band (AN2) were integrated to calculate FCH4 and FCO2 based on Eq. (2). Because the intensity of the upper band of v1–2v2(CO2) is higher than that of the lower band (Fig. 2), we calculated the peak area of the upper band to obtain FCO2; the uncertainty in peak area calculation can be reduced in this way. The wavenumber ranges for the calculations of ACH4, ACO2, and AN2 are from 2880 to 2950 cm−1, from 1375 to 1400 cm−1, and from 2310 to 2345 cm−1, respectively (Fig. 2).

3 Results

3.1 CH4–CO2–CO–N2 system

As shown in Fig. 3a, the characteristic band positions of all the investigated gases shift slightly to lower wavenumber with increasing pressure. For FCH4 and FCO2, they increase with rising pressure in the low-pressure range (e.g., < 15 MPa; Fig. 3b). For example, FCH4 increases from 5.22 at 1 MPa to 6.37 at 15 MPa; FCO2 increases from 1.46 at 1 MPa to 1.70 at 10 MPa (Table 1). At higher pressures, neither FCH4 nor FCO2 shows significant variations.

Fig. 3
figure 3

a Typical Raman spectra of CH4–CO2–CO–N2 mixtures collected at pressures between 1 and 60 MPa and at constant temperature of 22 °C and b the obtained Raman quantification factors of CH4 and CO2 as a function of pressure at 22 °C. Data plotted are those listed in Table 1. Previous works of Wopenka and Pasteris (1987), Chou et al. (1990), Seitz et al. (1993, 1996) and Xi et al. (2014) are also shown for comparison

Full size image
Table 1 Calculated Raman quantification factors of N2, CH4, CO and CO2 at pressures from 1 to 60 MPa and at constant temperature of 22 °C
Full size table

3.2 Pure CH4 system

Figure 4a shows the v1(CH4) spectra collected at pressures from 0.2 to 136 MPa and at constant temperature of 22 °C. The v1(CH4) peak position shifts from 2916.43 cm−1 at 0.2 MPa to 2908.81 cm−1 at 136 MPa (Table 2). Figure 4b further demonstrates the dependence of v1(CH4) peak position on pressure in pure CH4. In this study, the v1(CH4)-P curve can be expressed as:

$$\begin{aligned} & \upsilon_{1} ( {\text{CH}}_{ 4} )= 8.09 \times 10^{ - 8} \times P^{4} - 3.13 \times 10^{ - 5} \times P^{3} + 4.54 \times 10^{ - 3} \times P^{2} - 0.3 0\times P + 2916.78 \\ & (R^{2} = 0.998) \\ \end{aligned}$$
(3)
Fig. 4
figure 4

a Typical Raman spectra of pure CH4 collected at pressures between 0.2 and 136 MPa and at constant temperature of 22 °C. Neon emission lines are also collected to calibrate the v1(CH4) peak position and b the dependence of v1(CH4) peak position on fluid pressure at 22 °C. Data plotted are those listed in Table 2. Previous works of Chou et al. (1990), Seitz et al. (1996), Thieu et al. (2000), Hansen et al. (2001), Jager and Sloan (2001) and Lu et al. (2007) are also shown for comparison

Full size image
Table 2 The measured and calculated v1(CH4) peak position for pure CH4 at pressures from 0.2 to 136 MPa and at constant temperature of 22 °C
Full size table

4 Discussion

4.1 Comparisons with previous experimental calibrations

Previously experimental calibrations of FCH4 and FCO2 were also carried out at room temperatures (e.g., Wopenka and Pasteris 1987; Chou et al. 1990; Seitz et al. 1993, 1996). Wopenka and Pasteris (1987) collected the spectra of various gas mixtures with known composition at pressures of < 1.5 MPa. The FCH4 and FCO2 were reported to be 6.7 ± 0.15 and 1.52 ± 0.047, respectively (Wopenka and Pasteris 1987). The experiments of Chou et al. (1990) and Seitz et al. (1993) were carried out in the same laboratory as those for Wopenka and Pasteris (1987). Chou et al. (1990) collected the spectra of equimolar CH4–N2 mixture at pressures up to 65 MPa. They found that FCH4 increases with rising pressure at < ~7 MPa and reaches a relatively stable value of ~ 7.1 above 7 MPa. Seitz et al. (1993) obtained similar FCH4 of 7.39 ± 0.20. It should be noted that they found FCH4 was independent of composition in the CH4–N2 mixtures, given that the pressure is high enough (e.g., > 15 MPa). Our experiments confirmed that FCH4 and FCO2 are dependent on fluid pressure at low pressure, but keep relatively constant at high pressure (Fig. 3b). This phenomenon could be interpreted in the context of the molecular interactions (Seitz et al. 1993). As listed in Eq. (2), the Raman quantification factor is the product of the instrumental efficiency and the molecular parameters. Through monitoring the F-factor (e.g., FCH4), the change in the relative scattering efficiencies of the two components (i.e., CH4 and N2) can be monitored as a function of the molecular environment, since all other parameters are held constant (Seitz et al. 1993). That is to say, the effect of molecular interactions at low pressures is stronger than those at high pressures. Therefore, before applying the F-factor to measure the compositions of natural FIs, the experimental calibrations must be carried out in a broad pressure range that allows the determination of the steady F-factor.

Xi et al. (2014) obtained FCH4 (9.56) and FCO2 (0.86) for another spectrometer; the quantification factors were reported to be independent of pressure and fluid composition at pressures from 5 to 10 MPa. However, the reported FCH4 is more than 30% higher than those reported in Chou et al. (1990) (Fig. 3b). Because the FCO2 of Wopenka and Pasteris (1987) was obtained at low pressures that the molecular effect is significant, the experimental calibrations of Seitz et al. (1996) (FCO2 = 1.43 at > 10 MPa) were chosen for comparison. It can be seen that the FCO2 value of Xi et al. (2014) is ~ 40% lower than that of Seitz et al. (1996) (Fig. 3b). Our results confirmed that the F-factors obtained in different laboratories are different (Fig. 3b). This can be ascribed to the different instrumental efficiencies [c.f., Eq. (2)] for different Raman spectrometers. Therefore, the F-factors are quite laboratory-specific. Carefully experimental calibrations of F-factors should be carried out before applying this method to natural FIs. If a Raman spectrometer is well calibrated, the compositions of the gas mixtures in fused silica capillary capsules (FSCCs) (e.g., Chou et al. 2008; Wang et al. 2011) can be determined. Such FSCCs can be used as reference samples for other laboratories where the Raman spectrometer has not been calibrated yet.

As shown in Fig. 4b, the reported v1(CH4)-P curves are quite different (e.g., Chou et al. 1990; Seitz et al. 1996; Thieu et al. 2000; Hansen et al. 2001; Jager and Sloan 2001; Lu et al. 2007). This discrepancy was ascribed to the use of different reference standards for the calibration of the measured v1(CH4) wavenumber (Lu et al. 2007). However, the reported v1(CH4)-P curves are still different even the same reference standard was chosen (c.f., Thieu et al. 2000; Lin et al. 2007). To eliminate such discrepancy, Lu et al. (2007) proposed to calculate the difference (D) between the wavenumbers of v1(CH4) at elevated pressure (vp) and near-zero pressure (v0).

$$D = \upsilon_{p} - \upsilon_{0}$$
(4)

Then, D was used as the spectral parameter to construct the calibration curve of pressure. Lu et al. (2007) claimed that their D–P curve is a “unified equation” for the calculation of CH4 pressure in the CH4–H2O and CH4 systems. This is true in the low-pressure range (e.g., < 35 MPa), whereas large disagreement exists in the high-pressure range (e.g., > 35 MPa) [see Fig. 4 of Lu et al. (2007)]. In addition, to obtain the accurate vo value, one can just collect the spectra of the low-pressure CH4 gas (e.g., < 0.1 MPa) and determine the v1(CH4) wavenumber through peak fitting. Again, different laboratories may have different vo values due to the selection of different reference standards for the calibration of the Raman spectrometer [see Table 2 of Lu et al. (2007)]. In conclusion, after accurate determination of the laboratory-specific v0, the equation of Lu et al. (2007) can be used to calculate the pressure of the CH4-dominated vapor phase in FIs, if the pressure is below 35 MPa. However, the application of the D–P curve can result in large error, if the pressure of CH4-dominated vapor phase is higher than 35 MPa.

4.2 Application to natural FIs

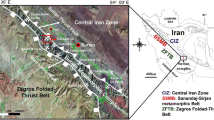
The Lower Silurian Longmaxi Formation is mainly composed of black shales in the Sichuan Basin, southwestern China (Li et al. 2013, 2018; Yang et al. 2019). It is also one of the most important shale gases playing in China at present (Jia et al. 2012; Zou et al. 2015; Jin et al. 2016; Ran et al. 2016). Many studies are focused on the current fluid pressure in the Longmaxi shales (e.g., Zou et al. 2015; Jin et al. 2016; Jiao et al. 2018; Wang et al. 2019), whereas the variation of paleo-fluid pressure has rarely been discussed. Shale gas is different from conventional natural gas in that the formation itself is both the source and the reservoir. Given their source rock nature, the investigation of the paleo-fluid pressure within shales can provide important information on the generation, migration, and accumulation of hydrocarbons. FIs record the T–P conditions of fluid processes in the presence of water and other fluids (e.g., Roedder and Bodnar 1980; Bergman and Dubessy 1984; Roedder 1984). In black shales, FIs can only be observed in some vein minerals, such as calcite and quartz. In this study, the quartz-calcite vein samples of the Lower Silurian Longmaxi shale were collected from an exploratory well (No. X) in southern Sichuan Basin, southwestern China (Fig. 5). The sampling depth is ~ 3830 m. FIs in the quartz veins were observed under a conventional polarizing microscope. Then, typical FIs were chosen for in situ Raman spectroscopic analyses.

Fig. 5
figure 5

A geological map showing the location of Well X [modified after National 1:200,000 Geological Map (H-48-23)]. b The magnification of the black-rectangle-marked area in a

Full size image

As shown in Fig. 6a, b, two types of FIs, two-phase aqueous inclusions (type I) and single-phase gas inclusions (type II) were identified in the quartz veins. For type I inclusions, the filling degree of the vapor phase ranges from 0.05 to 0.6. The size ranges from 1 to 25 µm. In situ Raman spectroscopic analyses show that the vapor phase is mainly composed of pure CH4 (Fig. 6c; Table 3). The vapor pressure at room temperature can reach 45.25 MPa [c.f., Eq. (3)]. As to type II inclusions, they generally show cogenetic features with type I inclusions. The size ranges from 0.5 to 15 µm. In most cases, the gas inside type II FIs is pure CH4. Only a few contain minor CO2 (4.4–7.4 mol%; Fig. 6d; Table 3). This type of FIs is characterized by extremely high pressure at room temperature; in situ Raman quantification yields CH4 pressure ranging from 103.65 to 128.35 MPa. As discussed in Sect. 4.1, FCH4 and FCO2 are pressure dependent at low pressures. Before applying F-factor to measure the molar ratio of CH4 and CO2, the internal pressure of the FIs should be estimated so that proper F-factor values could be chosen. Because the CH4/CO2 ratio is unknown, it is impractical to get the exact internal pressure (c.f., Chou et al. 1990). Here, we propose a method to estimate the pressure for CH4-dominated gas mixtures at room temperature. Chou et al. (1990) showed that the presence of N2 results in a high-wavenumber shift of the v1(CH4) band for N2–CH4 mixtures at constant total pressure (see Fig. 7). Therefore, the v1(CH4)-P curve for pure CH4 system can provide the minimum total pressure of CH4–N2 mixtures. If this pressure is higher than the threshold pressure for F-factor (i.e., 15 MPa for FCH4 and FCO2 in Fig. 3b), then we can apply the steady F-factors (i.e., FCH4 = 6.42 and FCO2 = 1.69 in this study) to measure the molar ratio of the N2–CH4 mixtures. For CH4–CO2 mixture, Seitz et al. (1996) found that the addition of < 50 mol% CO2 does not change the v1(CH4)-P curve significantly (see Fig. 1a). Therefore, the v1(CH4)-P curve for pure CH4 system can be used to measure the total pressure of CH4-dominated CH4–CO2 mixtures. Based on the above discussion, the molar ratio of CH4/CO2 can be measured using the steady F-factors, and the fluid pressure of CH4–CO2 mixtures can be obtained using Eq. (3) in this study (Table 3).

Fig. 6
figure 6

Microscopic photographs and in situ Raman spectra of typical FIs hosted in quartz veins from Silurian Longmaxi Formation black shales. a, b Two-phase aqueous FIs coexist with single-phase gas FIs; c Typical spectra for two-phase aqueous FIs. The room-temperature pressure of the vapor phase is also shown. v2-H2O and vs-H2O are the bending and stretching vibration modes of water, respectively, and d typical spectra of single-phase gas FIs indicate the presence of CH4–CO2 mixture and pure CH4 within these FIs. Raman quantification of the composition and room-temperature pressure are also shown. Data plotted are those listed in Table 3. V vapor phase, Aq aqueous phase

Full size image
Table 3 Pressures and compositions of the vapor phase of investigated FIs at room temperature and the pressures of type II inclusions at 200 °C
Full size table
Fig. 7
figure 7

A diagram showing the burial history of Well X. The gas window and the maximum burial depth are marked using red lines and blue lines, respectively

Full size image

Coexistence of two-phase aqueous and single-phase CH4 inclusions suggests that these fluid inclusions were trapped in the two-phase immiscible field (Fig. 6a, b; Fall et al. 2012). Under this circumstance, the homogenization temperatures for the two-phase aqueous inclusions represent trapping temperatures (Roedder 1984; Goldstein and Reynolds 1994). Unfortunately, homogenization experiments were not conducted in this study, due to the high internal pressure of these FIs. However, the trapping temperature can still be estimated based on the composition of the hydrocarbon phase and the hydrocarbon generation theory. Firstly, CH4 in the FIs results from primary trapping instead of secondary pyrolysis of previously trapped oil or bitumen. If CH4 is the product of the pyrolysis of liquid hydrocarbons, residual carbon or pyrobitumen should occur on the walls of these FIs (c.f., Xiong et al. 2004). Also, in situ Raman spectroscopic analyses will be hampered by strong fluorescence due to the presence of aromatic molecules (Khorasani 1987; Dutkiewicz et al. 2003). However, these phenomena were not observed in this study. Secondly, the formation of thermogenic dry gas (e.g., > 95 mol% CH4) generally occurs at > 200 °C (Ro > 2%; Tissot and Welte 1984; Hunt 1996). As described earlier, the vapor phase of the investigated FIs is mainly composed of CH4. Although the exact trapping temperature of these CH4-rich FIs is not available at present, a minimum temperature of 200 °C is reasonable. Compared with the burial history of Well X, these FIs should be formed between Early Triassic and Late Cretaceous (Fig. 7).

For type II FIs, the V-x properties can be obtained based on in situ Raman spectroscopic measurements; the composition and pressure at 22 °C are listed in Table 3. For pure CH4 system, the fluid pressure at 200 °C can be calculated on NIST Chemistry WebBook. As to the CH4–CO2 system, the fluid pressure at 200 °C can be obtained based on the thermodynamic models of Bowers and Helgeson (1983) and Bakker (1999). The calculated results are listed in Table 3. It can be seen that the fluid inclusions were trapped in the high temperature (> 200 °C), high pressure (> 218.03–256.82 MPa), and CH4-saturated immiscible fluid.

As shown in Fig. 7, the formation temperature of Lower Silurian reached 200 °C during Early Triassic and increased to its peak temperature of ~ 220 °C during Late Cretaceous. After Late Cretaceous, this area experienced significant uplift, and the current formation temperature is ~ 120–130 °C. The exact timing of fluid trapping is not available due to the lack of the homogenization temperature of type I FIs. However, the maximum burial depth of Lower Silurian is ~ 6450 m, corresponding to a hydrostatic pressure of 64.5 MPa. Therefore, we can still infer that the paleo-pressure coefficient of the Longmaxi Formation can reach > 3.38 between Late Permian and Late Cretaceous. The presence of such paleo-overpressure may result from hydrocarbon generation (Ungerer et al. 1983; Spencer 1987; Liu et al. 2009) and may account for the expulsion of CH4 to adjacent reservoir rocks.

5 Conclusions

Pure CH4 and CH4–CO2–CO–N2 mixture systems were loaded into fused silica tubing and pressurized to 136 MPa at 22 °C. In situ Raman spectra of these gases were collected and processed to address the potential of using Raman spectroscopic analyses to determine the pressure and molar ratio of CH4–CO2 mixtures in natural FIs. The major contributions are:

  1. 1.

    The Raman peak area ratios of CH4 and CO2 can be used to determine the molar ratio of CH4 and CO2 in natural FIs. However, before applying this approach, an estimation of the total pressure is needed. The v1(CH4) peak position can be used to calculate the pressure of CO2–CH4 mixture if the fluid is dominated by CH4. If the pressure is higher than 15 MPa, then an accurate determination of the CO2/CH4 ratio can be obtained.

  2. 2.

    The v1(CH4) peak position shifts to lower wavenumber with increasing pressure at constant temperature. The v1(CH4)-P curve is constructed. Careful calibration should be taken before applying this curve to measure CH4 pressure in natural FIs, because reported v1(CH4)-P curves are different, especially in the high-pressure range.

  3. 3.

    High-pressure CH4-rich FIs are reported in quartz veins from Longmaxi black shales. The composition and pressure of these FIs are quantified through in situ Raman spectroscopic analyses. The trapping pressure of the CH4-saturated fluid can reach > 218.03–256.82 MPa, which provides direct evidence for the paleo-overpressure of source rocks during methane generation.