ASYMMETRIC SOLAR WIND ELECTRON DISTRIBUTIONS

The theoretical framework of the present paper is the self-consistent weak turbulence equations that describe nonlinear interactions among Langmuir and ion-sound modes, as well as with the particles. In the present analysis, we resort to 1D approximation and assume that only electrostatic interaction is of importance. The equations of weak turbulence theory can be found in the papers by Yoon et al. (2006), Rhee et al. (2006), Pavan et al. (2009), and Ziebell et al. (2008, 2012). These consist of Langmuir and ion-sound wave kinetic equations and the particle (electron) kinetic equation. For the sake of completeness, we reproduce the fully 3D version of the self-consistent set of equations, although in the actual numerical computation only the 1D situation shall be considered,

$$\begin{eqnarray} \frac{\partial f_e}{\partial t} &=& \frac{\partial }{\partial {\bf v}}\cdot \left({\bf A}f_e+\vec{\vec{D}} \cdot \frac{\partial f_e}{\partial {\bf v}}\right), \nonumber \\ {\bf A} &=& \frac{e^2}{4\pi m_e}\int d{\bf k}\frac{\bf k}{k^2} \sum _{\sigma =\pm 1}\sigma \omega _{\bf k}^L\delta \big(\sigma \omega _{\bf k}^L-{\bf k}\cdot {\bf v}\big), \nonumber \\ \vec{\vec{D}} &=& \frac{\pi e^2}{m_e^2}\int d{\bf k} \frac{\bf kk}{k^2}\sum _{\sigma =\pm 1}\delta \big(\sigma \omega _{\bf k}^L-{\bf k}\cdot {\bf v}\big)I_{\bf k}^{\sigma L}, \nonumber \\ \frac{\partial I_{\bf k}^{\sigma L}}{\partial t} &=& \frac{\pi \omega _{pe}^2}{k^2}\!\!\int\!\! d{\bf v}\, \delta \big(\sigma \omega _{\bf k}^L\,{-}\,{\bf k}\cdot {\bf v}\big)\! \left( \frac{ne^2}{\pi }f_e\,{+}\,\sigma \omega _{\bf k}^L I_{\bf k}^{\sigma L}{\bf k}\cdot \frac{\partial f_e}{\partial {\bf v}}\right ) \nonumber \\ && {+}\frac{\pi }{2}\frac{e^2}{T_e^2} \sum _{\sigma ^{\prime },\sigma ^{\prime \prime }=\pm 1}\sigma \omega _{\bf k}^L \int d{\bf k}^{\prime }\frac{\mu _{{\bf k}-{\bf k}^{\prime }} ({\bf k}\cdot {\bf k}^{\prime })^2}{k^2{k^{\prime }}^2({\bf k}-{\bf k}^{\prime })^2} \nonumber \\ &&{\times} \delta \big(\sigma \omega _{\bf k}^L-\sigma ^{\prime }\omega _{{\bf k}^{\prime }}^L -\sigma ^{\prime \prime }\omega _{{\bf k}-{\bf k}^{\prime }}^S\big) \nonumber \\ && {\times} \big(\sigma \omega _{\bf k}^LI_{{\bf k}^{\prime }}^{\sigma ^{\prime }L} I_{{\bf k}{-}{\bf k}^{\prime }}^{\sigma ^{\prime \prime }S}\,{-}\,\sigma ^{\prime }\omega _{{\bf k}^{\prime }}^L I_{{\bf k}-{\bf k}^{\prime }}^{\sigma ^{\prime \prime }S}I_{\bf k}^{\sigma L} -\sigma ^{\prime \prime }\! \omega _{{\bf k}-{\bf k}^{\prime }}^LI_{{\bf k}^{\prime }}^{\sigma ^{\prime }L} I_{\bf k}^{\sigma L}\big) \nonumber \\ && {-}\frac{\pi e^2}{m_e^2\omega _{pe}^2}\sum _{\sigma ^{\prime }=\pm 1} \int d{\bf k}^{\prime }\int d{\bf v}\frac{({\bf k}\cdot {\bf k}^{\prime })^2}{k^2{k^{\prime }}^2} \nonumber \\ &&{\times} \delta \big[\sigma \omega _{\bf k}^L -\sigma ^{\prime }\omega _{{\bf k}^{\prime }}^L-({\bf k}-{\bf k}^{\prime })\cdot {\bf v}\big] \nonumber \\ && {\times} \bigg[\frac{ne^2}{\pi \omega _{pe}^2}\sigma \omega _{\bf k}^L\left(\sigma ^{\prime }\omega _{{\bf k}^{\prime }}^L I_{\bf k}^{\sigma L}-\sigma \omega _{\bf k}^L I_{{\bf k}^{\prime }}^{\sigma ^{\prime }L}\right) \nonumber \\ &&{\times} f_i-\frac{m_e}{m_i} \sigma \omega _{\bf k}^LI_{{\bf k}^{\prime }}^{\sigma ^{\prime }L} I_{\bf k}^{\sigma L}({\bf k}-{\bf k}^{\prime })\cdot \frac{\partial f_i}{\partial {\bf v}}\bigg], \nonumber \\ \frac{\partial I_{\bf k}^{\sigma S}}{\partial t} &=& \frac{\pi \mu _{\bf k}\omega _{pe}^2}{k^2}\int d{\bf v}\; \delta \big(\sigma \omega _{\bf k}^S-{\bf k}\cdot {\bf v}\big) \nonumber \\ &&{\times} \left[\frac{ne^2}{\pi }\,(f_e+f_i)+\sigma \omega _{\bf k}^L I_{\bf k}^{\sigma S}\left({\bf k}\cdot \frac{\partial }{\partial {\bf v}}\right) \left(f_e+\frac{m_e}{m_i}f_i\right)\right] \nonumber \\ && {+}\frac{\pi }{4}\frac{e^2}{T_e^2} \sum _{\sigma ^{\prime },\sigma ^{\prime \prime }=\pm 1}\sigma \omega _{\bf k}^L \int d{\bf k}^{\prime }\frac{\mu _{\bf k}[{\bf k}^{\prime }\cdot ({\bf k}-{\bf k}^{\prime })]^2}{k^2{k^{\prime }}^2({\bf k}-{\bf k}^{\prime })^2} \nonumber \\ && {\times} \delta \big(\sigma \omega _{\bf k}^S-\sigma ^{\prime }\omega _{{\bf k}^{\prime }}^L -\sigma ^{\prime \prime }\omega _{{\bf k}-{\bf k}^{\prime }}^L\big) \nonumber \\ && {\times} \big(\sigma \omega _{\bf k}^LI_{{\bf k}^{\prime }}^{\sigma ^{\prime }L} I_{{\bf k}{-}{\bf k}^{\prime }}^{\sigma ^{\prime \prime }L}\,{-}\,\sigma ^{\prime }\omega _{{\bf k}^{\prime }}^L I_{{\bf k}{-}{\bf k}^{\prime }}^{\sigma ^{\prime \prime }L}I_{\bf k}^{\sigma S} \,{-}\,\sigma ^{\prime \prime }\! \omega _{{\bf k}{-}{\bf k}^{\prime }}^LI_{{\bf k}^{\prime }}^{\sigma ^{\prime }L} I_{\bf k}^{\sigma S}\big), \nonumber\hspace{-6pt} \\ \end{eqnarray} \tag{ 1 }$$

where f_e is the electron VDF (normalized to unity, ∫dvf_e = 1) and $f_i=(\pi v_{Ti})^{-3/2}e^{-v^2/v_{Ti}^2}$ is the stationary ion VDF. The quantities I^σL_k and I^σS_k stand for Langmuir and ion-sound mode intensities, respectively, and are related to the total spectral fluctuating electric field energy density by

$$\begin{equation} \left<\delta {\bf E}^2\right>_{{\bf k},\omega } =\sum _{\sigma =\pm 1}\left[I_{\bf k}^{\sigma L}\delta \big(\omega -\sigma \omega _{\bf k}^L\big)+I_{\bf k}^{\sigma S} \delta \big(\omega -\sigma \omega _{\bf k}^S\big)\right]. \end{equation} \tag{ 2 }$$

In the above σ = ±1 designates the direction of the wave phase speed, the plus/minus denoting the forward/backward direction. The quantities m_e and m_i are electron and ion rest masses, respectively, ω²_pe = 4πne²/m_e represents the square of the plasma frequency, and v²_Te = 2T_e/m_e and v²_Ti = 2T_i/m_i are the squares of electron and ion thermal speeds, respectively, T_e and T_i being electron and ion temperatures, respectively. The wave dispersion relations for L (Langmuir) and S (ion-sound) waves are well known in the literature,

$$\begin{eqnarray} \omega _{\bf k}^L &=& \omega _{pe}\left(1+\frac{3k^2v_{Te}^2}{2\omega _{pe}^2}\right), \nonumber \\ \omega _{\bf k}^S &=& \frac{k^2c_S^2(1+3T_i/T_e)^{1/2}}{1+k^2\lambda _{{\rm De}}^2}. \end{eqnarray} \tag{ 3 }$$

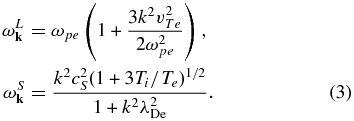
The quantity μ_k is defined by

$$\begin{equation} \mu _{\bf k}=k^3\lambda _{{\rm De}}^3\left(\frac{m_e}{m_i}\right)^{1/2} \left(1+\frac{3T_i}{T_e}\right)^{1/2}. \end{equation} \tag{ 4 }$$

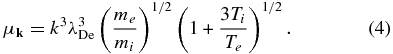
The physical meaning of the various terms in the particle (electron) kinetic equation and the wave kinetic equations for L and S modes has already been discussed in previous papers by Yoon and his colleagues (Yoon et al. 2006; Rhee et al. 2006; Pavan et al. 2009; Ziebell et al. 2008, 2012), so we shall not repeat them in full detail, but briefly, we shall only note that those terms dictated by the resonance condition delta function δ(σω^L_k − k · v) or δ(σω^S_k − k · v) represent linear wave–particle interactions, those dictated by $\delta (\sigma \omega {\bf k}^L -\sigma ^{\prime }\omega _{{\bf k}^{\prime }}^L-\sigma ^{\prime \prime }\omega _{{\bf k}-{\bf k}^{\prime }}^S)$ or $\delta (\sigma \omega {\bf k}^S-\sigma ^{\prime }\omega _{{\bf k}^{\prime }}^L -\sigma ^{\prime \prime }\omega _{{\bf k}-{\bf k}^{\prime }}^L)$ stand for nonlinear wave–wave resonant interactions, and finally the term associated with δ[σω^L_k − σ'ω_k'^L − (k − k') · v] depicts nonlinear wave–particle resonance.

We have solved the set of Equation (1) in 1D approximation for an initial electron VDF given by the combination of a core Maxwellian component and a beam population, which in 1D is given by

$$\begin{equation} f_e=\frac{1-n_b/n_e}{\pi ^{1/2}v_{Te}}e^{-v^2/v_{Te}^2} +\frac{n_b/n_e}{\pi ^{1/2}v_{Tb}}e^{-(v-V_b)^2/v_{Tb}^2}, \end{equation} \tag{ 5 }$$

where v²_Tb = 2T_b/m_e is the thermal spread associated with the beam electrons. In general the beam component is not observed for quiet-time solar wind, although during impulsive events such as the type III radio bursts, the electron beam is often observed together with enhanced Langmuir turbulence and electromagnetic radiation (Lin et al. 1981, 1986). The actual presence of a field-aligned beam component is not easy to detect by experimental means, however. In the present paper, we consider an initial beam component to facilitate the excitation of Langmuir turbulence so that we may allow faster dynamical evolution. Our purpose is to compare the long-time solution, not the initial VDF, with observed VDFs, so that the choice of admittedly somewhat arbitrary initial electron beam is immaterial in the end. In the computation, we therefore assume that the ratio of electron beam speed to background thermal speed is given by V_b/v_Tb = 4 for all the cases considered. We also assume that the initial Gaussian thermal spread associated with the beam component is equal to the background temperature, T_b = T_e.

Initial wave intensities are specified by requiring the balance of spontaneous and induced emission processes, which in 1D are specified by

$$\begin{eqnarray} \frac{ne^2}{\pi } &=& \frac{m_e\big(\omega _k^L\big)^2}{T_e}I_k^{\sigma L}, \nonumber \\ \frac{ne^2}{\pi }\,(f_e+f_i) &=& \frac{m_e\omega _k^L\omega _k^S}{T_e} \left(f_e+\frac{T_e}{T_i}f_i\right)I_k^{\sigma S}. \end{eqnarray} \tag{ 6 }$$

In the numerical analysis there are other physical parameters that must be specified. For instance, one of the crucial parameters is the so-called plasma parameter, g = 1/nλ³_De, which represents the inverse of the number of particles in the sphere of radius equal to the Debye length. Here, λ²_De = T_e/(4πne²) is the electron Debye length squared, T_e, n, and e being the electron temperature, ambient density, and unit electric charge, respectively. For a typical solar wind near 1 AU, the electron temperature is of the order 10⁴–10⁵ K, and the ambient density can be as low as 1 cm⁻³ and can reach up to ${\cal O}(10)$ cm⁻³, and sometimes even higher. When the plasma parameter g is computed on the basis of these quantities, we find that $g\sim {\cal O}(10^{-7})$ to ${\cal O}(10^{-5})$ or so. In the present weak turbulence simulation, the finiteness of the g parameter is crucial in that if we set g = 0 exactly, then all the terms corresponding to spontaneous thermal effects vanish—the term associated with the drag coefficient A in the electron kinetic equation, the term ne²f_e/π in the Langmuir wave kinetic equation, the term associated with $(\sigma ^{\prime }\omega _{{\bf k}^{\prime }}^L I_{\bf k}^{\sigma L}-\sigma \omega _{\bf k}^L I_{{\bf k}^{\prime }}^{\sigma ^{\prime }L})f_i$ in the nonlinear term of the Langmuir wave kinetic equation, and finally the term ne²(f_e + f_i)/π in the ion-sound wave kinetic equation. It was shown by Yoon et al. (2006) and Rhee et al. (2006) that without these terms, no suprathermal tail forms.

Often, the finiteness of the g parameter is related to the collisionality of the solar wind. Near 1 AU, it is often said that the solar wind is "collisionless." However, even though g may be small, it is nevertheless finite. The finiteness of g leads to the formation of suprathermal tails in the electron–Langmuir turbulence scenario. In the present analysis, we shall consider a slightly higher value of g than the actual observation so as to facilitate the numerical computation and to demonstrate the formation of an energetic tail within a reasonable timescale. Specifically, we shall consider g = 5 × 10⁻³. Another input parameter is the energetic-to-core electron density ratio, n_b/n_e. Observations of the solar wind near 1 AU and beyond show that the halo-to-core electron number density ratio is of the order ${\cal O}(10^{-2})$ or so (Maksimovic et al. 2005; Stverak et al. 2009). From this we choose the ratio n_b/n_e = 10⁻². We consider a range of the ratio of ion and electron temperature T_i/T_e: specifically, T_i/T_e = 1/15, 1/10, 1/7, 1/4, 1/2, and 1. Note that Yoon et al. (2005, 2006), Rhee et al. (2006), Ryu et al. (2007), and Gaelzer et al. (2008) all considered a fixed value of T_i/T_e sufficiently less than unity. In contrast, we consider T_i/T_e ranging from 1/15 to as high as 1.

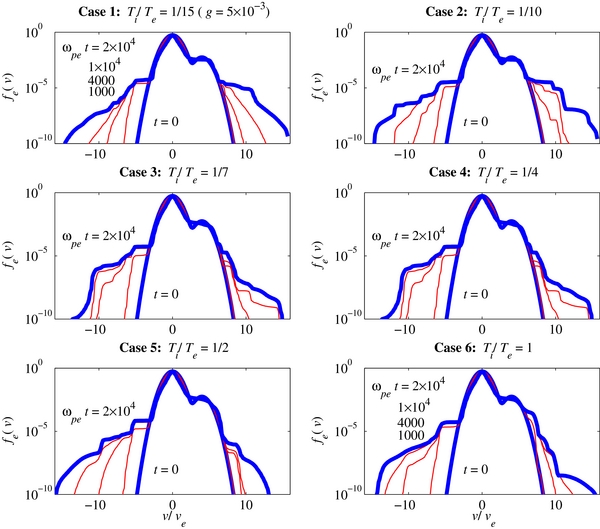
Figure 1 displays the electron VDFs for six different cases corresponding to (1) T_i/T_e = 1/15, (2) T_i/T_e = 1/10, (3) T_i/T_e = 1/7, (4) T_i/T_e = 1/4, (5) T_i/T_e = 1/2, and (6) T_i/T_e = 1, for initial input physical parameters n_b/n_e = 10⁻², V_b/v_Te = 4, and g = 5 × 10⁻³. The first two cases, namely, T_i/T_e = 1/15 and T_i/T_e = 1/10, show that over a long computational period (up to ω_pet = 2 × 10⁴), the initial core plus beam system evolved to a system composed of the core population, which did not undergo much change, plus a prominent pair of quasi-symmetric tail populations that emerged gradually over time. For cases (3) and (4), for which T_i/T_e = 1/7 and T_i/T_e = 1/4, respectively, it can be seen that the tail formation is slightly reduced over the same time period when compared with the previous two cases. Note that the two cases appear nearly identical, which shows that the variation on T_i/T_e in the range T_i/T_e = 1/7 to 1/4 appears to have little impact on the change in the dynamics. It can also be seen that the forward and backward components are slightly asymmetric, with the backward tail slightly more prominent than the forward tail. The case of T_i/T_e = 1/2, on the other hand, shows that it definitely has more influence on the change in the dynamics. Specifically, it can be seen that the asymmetry has increased when compared with the previous two cases. The final case of T_i/T_e = 1 shows a further increase in the asymmetry. From the results shown in Figure 1, it is clear that varying T_i/T_e affects the degree of asymmetry—the higher the ratio, the more prominent is the asymmetry.

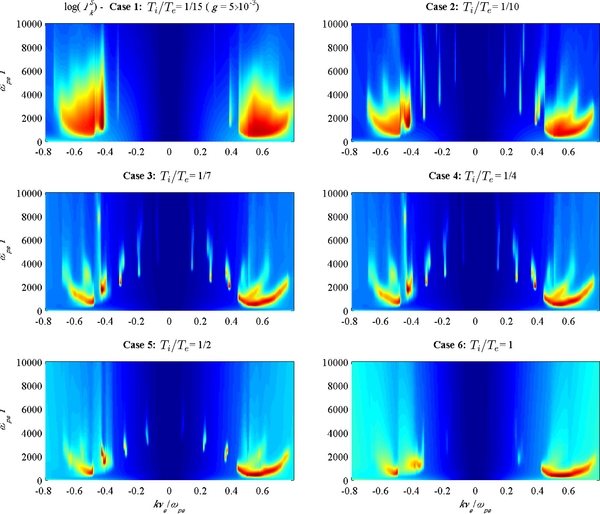
Zoom In Zoom Out Reset image size

In order to understand the physical reason why the change in the ion-to-electron temperature ratio should have such a definite impact on the formation of the asymmetric tail distribution, we now plot the Langmuir wave intensity as a function of normalized wave number kv_Te/ω_pe and normalized time ω_pet. For the case of low T_i/T_e = 1/15, one may observe that, after an initial excitation of bump-in-tail instability near kv_Te/ω_pe ∼ 1/4, the subsequent evolution of the spectrum involves the backscattering to negative k mode and the formation of the so-called Langmuir condensate near small k. It can be seen that the wave spectrum is rather smooth in k space, and near the end of the temporal plotting range, ω_pet = 10⁴, the level of Langmuir wave intensity in the positive (k > 0) and negative (k < 0) wavenumber space is comparable in strength.

For the next three cases, T_i/T_e = 1/10, 1/7, and 1/4, one can see that the spectrum develops fine structure in k space, and the backward Langmuir wave component shows increasingly higher intensity as the case moves from T_i/T_e = 1/10, to T_i/T_e = 1/7, to T_i/T_e = 1/4. This explains why the negative v tail becomes more and more prominent. Note that the cases of T_i/T_e = 1/7 and T_i/T_e = 1/4 are nearly identical, but upon careful examination, one can discern small but noticeable differences in the fine-structure spectrum. Finally, the trend of increasing negative k mode intensity continues as the case moves to T_i/T_e = 1/2 and to T_i/T_e = 1. It is interesting to note that for T_i/T_e = 1 the fine structure has somewhat dissipated and the Langmuir wave spectrum again looks rather smooth in k space.

To further understand the dynamics, let us examine the wave spectrum associated with the ion-sound mode. Shown in Figure 3 is the plot of ion-sound spectral intensity in the same format as Figure 2. For the first case of T_i/T_e = 1/15, for which the linear theory predicts that ion-sound damping should be small, it can be seen that the ion-sound turbulence is generated via three-wave decay instability, in both the forward and backward propagation directions. The strong excitation of S mode via the decay process takes the wave energy out of L mode, and as such the corresponding Langmuir wave spectrum shown in Figure 2 case (1) indicates relatively low L mode wave energy when compared to other cases. Moving on to case (2) where T_i/T_e = 1/10, for which the Landau damping rate should increase slightly, it can be seen from Figure 3 case (2) that the ion-sound mode intensity has decreased somewhat when compared to case (1). Also, note the appearance of fine structure in the S mode spectrum. This is consistent with similar fine structure in the corresponding L mode. As T_i/T_e increases, Figure 3 cases (3)–(6) show steady decline in the S mode wave intensity. Note that in the final case (6), for which Landau damping of S mode should be the highest among the cases considered, the fine structure in the spectrum has decreased, which is again consistent with the corresponding L mode spectrum.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

We have also repeated the same set of calculations for lower values of the g parameter. As expected, the formation of the tails in the case of lower values of g was found to be less pronounced over the same computational timescale. Upon examining the Langmuir wave and ion-sound mode spectral intensities in the case of lower values of g, we found that the overall spectral features were consistent with the case of g = 5 × 10⁻³. However, the important consequence of a lower g parameter seems to be the delay in the formation of the energetic tail population. We have not shown numerical examples in order to avoid repetitions. However, it is important to note that as long as a finite g value is chosen, eventually the energetic electron population will be generated by the Langmuir turbulence process. As a matter of fact, Yoon (2011, 2012a, 2012b) and Yoon et al. (2012) showed that the balance of spontaneous and induced processes will always produce the energetic tail population in the time-asymptotic state, t → ∞, regardless of the value of g.