Abstract
Attosecond transient absorption is an ultrafast technique that has opened the possibility to study electron dynamics in condensed matter systems at its natural timescale. The extension to the x-ray regime permits one to use this powerful technique in combination with the characteristic element specificity of x-ray spectroscopy. At these timescales, the coherent effects of the electron transport are essential and have a relevant signature on the absorption spectrum. Typically, the complex light-driven dynamics requires a theoretical modeling for shedding light on the time-dependent changes in the spectrum. Here we construct a semiconductor Bloch equation model for resolving the light-induced and core-electron dynamics simultaneously, which enables to easily disentangle the interband and intraband contributions. By using the Bloch model, we demonstrate a universal feature on attosecond x-ray transient absorption spectra that emerges from the light-induced coherent intraband dynamics. This feature is linked to previous studies of light-induced Fano resonances in atomic systems.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The revolution of producing pulses as short as several attoseconds (10−18 s) has opened the door of observing the fast motion of electron in complex systems and exploring a new quantum realm at unprecedented time scales. Attosecond transient absorption (ATA) is a ultrafast technique resulting from such technology. ATA has been successfully applied to studies of electron dynamics in material systems, allowing to understand petahertz conductivity changes in dielectrics [1], tunneling excitation induced by intense laser pulses [2], sub-femtosecond dynamics of both holes and electrons in complex semiconductor materials [3], among other interesting ultrafast studies [4–8].
ATA consists in a pump-probe scheme, see figure 1, in which the pump pulse, typically an infrared (IR) pulse, drives the dynamics under investigation, while the absorption of the attosecond probe pulse is measured at different time delays with respect to the pump pulse. Both pulses are synchronized, as the pump pulse is also used to generate the attosecond pulse via high-order harmonic generation (HHG). Recent developments for HHG sources driven by few-cycle mid-IR lasers have allowed the production of attosecond pulses in the soft x-ray regime [9, 10], and the possibility to perform x-ray spectroscopy with such short pulses [11, 12]. This offers the possibility to determine local chemical state and electron configuration, spin states, coordination number, and local structural geometry. The extension of ATA into the soft x-ray regime is a powerful technique for condensed-matter systems, as one may envision to resolve electron dynamics at different elements and investigate attractive functional materials for optical applications such as solar energy harvesting and energy storage.
Figure 1. Attosecond transient absorption spectroscopy. Scheme of the pump-probe scheme.
Download figure:
Standard image High-resolution imageThe interpretation of ATA requires theoretical modeling to correlate the absorption changes of the x-ray pulse with the induced dynamics driven by the pump pulse. ATA experiments at XUV photon energies have relied on time-dependent density functional theory approaches [13], which has provided good results in comparison with experiments [5, 8]. However, the disentanglement of intraband and interband dynamics is not straightforward and adds an extra difficulty in the interpretation of the numerical results.
On the other hand, semiconductor Bloch equations (SBE) [14–17] have been successfully applied to describe the nonlinear response of semiconductors and two-dimensional materials under the interaction of intense IR and mid-IR laser pulses [18–23], and also to model ultrafast studies [6]. This many-body theory offers clear advantages for understanding and interpreting the induced complex dynamics, such as separating the intraband and interband contribution as well as reducing the numerical effort. There is still an ongoing debate about the underlying mechanisms of high-harmonic generation in solids and their intrinsic interband and intraband nature [24–27]. In this context, theoretical approaches that allow to disentangle both contributions are desirable.
In this work we present an extension of the standard SBE theory to the x-ray regime, named core-state-resolved Bloch equations (cBE), by including core-hole states. Using cBE, the induced dynamics driven by the IR pump and the x-ray probe pulse can be efficiently resolved. We demonstrate a universal feature of the pump-induced intraband dynamics on the attosecond x-ray transient absorption spectra in condensed-matter systems. This intraband effect is originated from the coherent lightwave electron transport prior to decoherence by scattering interactions or core-hole decay, and it can be connected to previous works on light-induced Fano spectral lineshapes in atomic systems [28]. This effect is important when the time of the attosecond excitation or the core-hole decay overlaps with the IR laser pulse. We also discuss the importance of this effect on ultrafast studies with mid-IR wavelengths or physical systems with high conductivity properties.
2. Theory
2.1. Core-state-resolved Bloch equations
We start from the SBE Hamiltonian expressed in second quantization
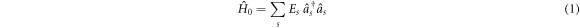
in which the canonical operators satisfy the anticommutator relations  and
and  , and Es is the energy of an electron in the state s. The electric field coupling, in the length gauge, is written as
, and Es is the energy of an electron in the state s. The electric field coupling, in the length gauge, is written as
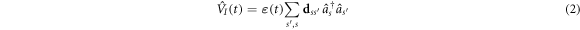
in which  is the electric field and
is the electric field and  stands for the dipole matrix element between states s and
stands for the dipole matrix element between states s and  . Our time-dependent Hamiltonian is
. Our time-dependent Hamiltonian is  and describes the dynamics of our many-body quantum state. By evolving the operators, within the Heisenberg picture, we find the equation
and describes the dynamics of our many-body quantum state. By evolving the operators, within the Heisenberg picture, we find the equation

We define the time-dependent density matrix elements, evolving from an initial state  , from the mean value of the canonical operator coherences [17]
, from the mean value of the canonical operator coherences [17]

in which we explicitly separate the quasi-momentum k from other quantum numbers, such as the spin and the energy of the band. Using equation (4), the SBE is cast as

being  . Here, we use the properties of the Bloch waves,
. Here, we use the properties of the Bloch waves,  , to separate the dipole matrix elements using the relation [29]
, to separate the dipole matrix elements using the relation [29]
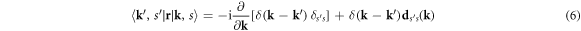
where we define

The first term of the dipole matrix element (6), which emerges from intraband transitions, plays a significant role in the density matrix coherences of the system, especially when it is driven by mid-IR laser pulses as we will show in the following.
In general, equation (5) accounts for all the energy bands of the system, although it is sufficient to truncate the sum to those bands in which the main dynamics is comprised. In simulating the dynamics in an attosecond x-ray transient absorption experiment, the coupling of the valence and conduction bands close to the Fermi level is driven by the IR pulse, while the coupling of core-electron bands and the bands close to the Fermi level is driven by the x-ray pulse. A certain numerical difficulty comes from the fact that both pulses represent two different timescales. However the interaction with the high-frequency nearly-resonant pulse can be described within the rotating-wave approximation, i.e. averaging the fast x-ray carrier oscillations. The electric field is composed by the sum of the IR,  , and the x-ray pulse,
, and the x-ray pulse,  . The x-ray pulse is described as
. The x-ray pulse is described as  , where gx(t) is a slowly-variant envelope function and ωx is the central frequency of the x rays. Defining the labels i, j, k, .. for energy bands close to the Fermi level and a, b, c, ... for core- and inner-shell bands, we obtain the core-state-resolved Bloch equations as
, where gx(t) is a slowly-variant envelope function and ωx is the central frequency of the x rays. Defining the labels i, j, k, .. for energy bands close to the Fermi level and a, b, c, ... for core- and inner-shell bands, we obtain the core-state-resolved Bloch equations as

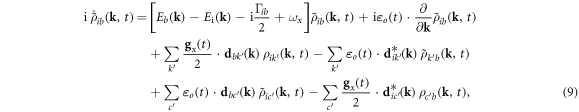
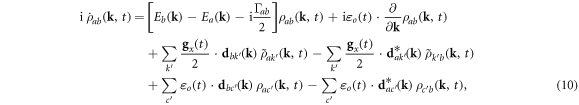
where we perform the phase transformation  and introduce the dephasing and relaxation terms Γ. Within the density matrix formalism, scattering effects accounting for electron–electron and electron–phonon interactions are included by dephasing or relaxation terms [16]. In ATA studies, the explored time scales are at most few femtoseconds and most scattering effects do not play a major role in the dynamics. For example, in non-equilibrium photo-carriers excitation studies, electron–electron scattering effects in graphite are found to be around 30 fs [30] and in monolayer MoSe2 are found to be around hundreds of femtoseconds [31]. On the other hand, relaxation terms arisen from core-hole decays must be included. Core-hole relaxations are in the order of hundreds of attoseconds to few femtoseconds, mainly triggered by Auger or fluorescence transitions.
and introduce the dephasing and relaxation terms Γ. Within the density matrix formalism, scattering effects accounting for electron–electron and electron–phonon interactions are included by dephasing or relaxation terms [16]. In ATA studies, the explored time scales are at most few femtoseconds and most scattering effects do not play a major role in the dynamics. For example, in non-equilibrium photo-carriers excitation studies, electron–electron scattering effects in graphite are found to be around 30 fs [30] and in monolayer MoSe2 are found to be around hundreds of femtoseconds [31]. On the other hand, relaxation terms arisen from core-hole decays must be included. Core-hole relaxations are in the order of hundreds of attoseconds to few femtoseconds, mainly triggered by Auger or fluorescence transitions.
2.2. Attosecond transient absorption
ATA is based on a time-resolved scheme. A pump IR pulse excites the system inducing the dynamics to be investigated. Then, with a controlled time delay with respect to the pump pulse, a second XUV/x-ray pulse, of only several to hundreds of attoseconds, propagates through the system. By measuring the absorption of the probe pulse with and without the pump pulse, one is able to retrieve information of pump-induced dynamics. It is important to take into account the broad bandwidth of the probe pulse and to model the response of the system at such short timescales for calculating the ultrafast absorption.
In the recent years, the theoretical modeling for calculating ATA spectra has been developed, first in atomic systems [32], and then extended to condensed-matter systems [4]. The ultrafast absorption can be calculated via the so-called response function
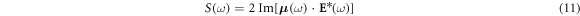
for positive frequencies ω > 0, where E and  stands for the Fourier transform of the electric field and dipole response of the system, respectively. The dipole response of the system is defined as
stands for the Fourier transform of the electric field and dipole response of the system, respectively. The dipole response of the system is defined as
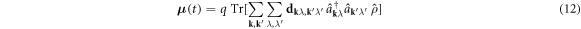
q is the charge of the electron. Since we are interested in the absorption of the XUV/x-ray pulse, the main contribution in the high-frequency region of the dipole response involves transitions between core sates and states near the Fermi level, and is given by
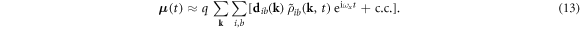
By integrating the cBE equations (8)–(10), we compute the response function given by equation (11) at the end of the simulation, and from the response function we calculate the absorption of the system using the relation [32]
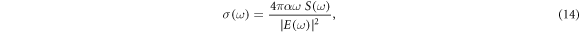
where α is the fine-structure constant.
2.3. cBE theory as time-dependent configuration interaction singles (TD-CIS)
The derivation of the SBE and cBE theory is based on creation and annihilation operators and is different from other many-body approaches used in condensed-matter systems to calculate the electronic properties. In this section we show the relation of a SBE theory with a TD-CIS, in which a configuration interaction expansion with single excitations is evolved in time by integrating the time-dependent Schrödinger equation.
Several TD-CIS approaches have been developed in these recent years with the aim of describing complex systems interacting with ultrashort light pulses [33–37]. One of the main advantages of these approaches is the possibility to account for electron correlations in a time-dependent framework. Here we re-interpret the SBE equations (5) from a TD-CIS perspective.
In Hartree–Fock theory, the Bloch orbitals with periodic conditions satisfy the hartree–fock operator
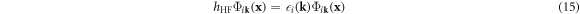
in which the wavefunction is given by
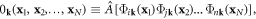
where ![$\hat{A}[]$](https://content.cld.iop.org/journals/1367-2630/21/4/043029/revision2/njpab1311ieqn15.gif) stands for the antisymmetry operator. The total electron density of the periodic system in the ground state is then
stands for the antisymmetry operator. The total electron density of the periodic system in the ground state is then

In order to simplify the TD-CIS interpretation, we assume a physical system at temperature zero and the conduction and valence bands are well separated in energy at the Fermi energy level.
When the system is interacting with an external time-dependent electric field, it is convenient to cast the total Hamiltonian as
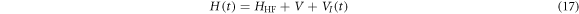
in which we define the Hartree–Fock Hamiltonian as  , where the sum j runs over all electrons in the occupied orbitals, while V is the difference between the Hamiltonian with no external field and the Hartree–Fock Hamiltonian. Following the recipe of TD-CI approaches, the solution of the evolving system is expanded as
, where the sum j runs over all electrons in the occupied orbitals, while V is the difference between the Hamiltonian with no external field and the Hartree–Fock Hamiltonian. Following the recipe of TD-CI approaches, the solution of the evolving system is expanded as
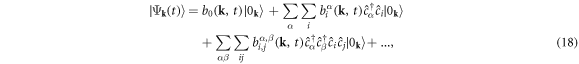
where  and
and  stand for the annihilation and creation operator of orbitals, eigenstates of the Hartree–Fock Hamiltonian. The order of the truncation depends on the problem under study. For example, first-order truncation will be sufficient for investigating laser-induced intraband dynamics of electron-hole pairs, while Pauli blocking effects, from different energy bands, will require a second-order truncation. Here we focus on the wavefunction created by single excitations, that is truncating to first excitations and assuming that second and higher excitations are zero. The ansatz is then reduced to
stand for the annihilation and creation operator of orbitals, eigenstates of the Hartree–Fock Hamiltonian. The order of the truncation depends on the problem under study. For example, first-order truncation will be sufficient for investigating laser-induced intraband dynamics of electron-hole pairs, while Pauli blocking effects, from different energy bands, will require a second-order truncation. Here we focus on the wavefunction created by single excitations, that is truncating to first excitations and assuming that second and higher excitations are zero. The ansatz is then reduced to
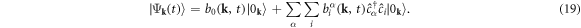
According to equation (4), we define the time-dependent TD-CIS coherences as

Note while the coherence of an electron in the conduction and a hole in the valence is just the multiplication of a single excitation amplitude with the unperturbed amplitude, coherences between single excitations involve a sum among all the holes or particle states. Now we need to find the time evolution of the TD-CI coherences. We insert the ansatz given by equation (19) into the time-dependent Schrödinger equation, and projecting over the different eigenstates of the basis ( and
and  ), we obtain the equations of motion (EOM) for the amplitudes
), we obtain the equations of motion (EOM) for the amplitudes
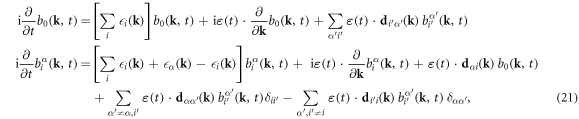
where we have defined
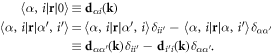
In the previous equations we have neglected electron correlations from the V potential of the Hamiltonian. Once we obtain the EOM for the amplitudes, after a cumbersome derivation, the time-dependent equations for the coherences (20) read as
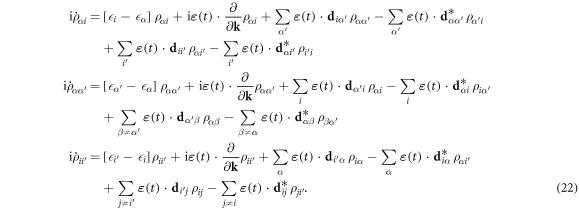
By separating the conduction and the valence bands in the SBE equations (5), we note that they are identical to the dynamical equations (22) found from the TD-CIS amplitudes. In conclusion, there is a correspondence between the SBE theory and the TD-CIS approach, in which the coherences (20) are built by tracing out the electron or hole of the single excitation. A similar correspondence is found by truncating the TD-CI expansion (18) at higher degree of excitations and finding the coherences via equations (20). This correspondence is particularly interesting to visualize the dynamical charge density of the system. In the following we further exploit this property to develop an analytical model to describe the intraband effects on ATA.
3. Intraband effects on ATA
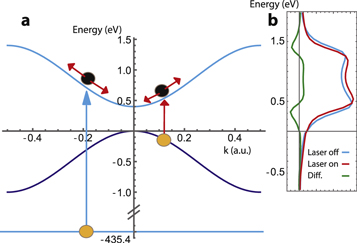
In this section we study the coherent effects on the transient absorption arisen from the intraband electron dynamics. Inspired by semi metals such as titanium disulfide, we consider a three-band system as depicted in figure 2(a), in which the crystal structure is a = 6.28 a.u., the energy bandgap is 0.4 eV, and the x rays are coupled only to the conduction band. The x-ray pulse has a central photon energy of 435.4 eV, and it is modeled by a gaussian envelope of 300 as FWHM. The IR laser pulse induces interband transitions from the valence to the conduction band as well as intraband transitions, i.e. it drives the excited electrons along the conduction band. The IR pulse has a 1850 nm wavelength (0.67 eV) and is modeled by a gaussian envelope of 12 fs FWHM (approximately 5 cycles). The intensity of the laser pulse is 3.3 × 1011 W cm−2. For simplicity, we assume the dipole transition between the valence and the conduction band equal to one atomic unit. We do not consider scattering damping factors, besides a core-hole decay with Γ = 0.30 eV (2.2 fs).
Figure 2. A three-band model for an attosecond transient absorption study. Scheme of the physical scenario. (a), A core electron is promoted to the conduction band by an ultrashort x-ray pulse and driven along by an mid-IR few-cycle pulse. Also, the laser could excite a valence electron into the conduction band and drive the created electron-hole pair along the corresponding bands. (b), Absorption spectra for the case with (red line) and with no (blue line) mid-IR laser pulse. We show the difference between laser-off and laser-on spectrum (green line) to emphasize the spectral changes.
Download figure:
Standard image High-resolution imageThe transient absorption is obtained by calculating the difference of absorption of the x rays with and with no laser pulse, and for different time delays between the two pulses. In figure 2(b) we show the absorption spectrum for a particular time delay. The blue line depicts the absorption of the system with no laser pulse. It extends over all the conduction band, showing two maxima connected with the absorption at the band edges. In the presence of the laser pulse, we observe a clear shift at the edges of the conduction band, while we observe an increase of absorption on the middle of the band. We further discuss these effects in the following.
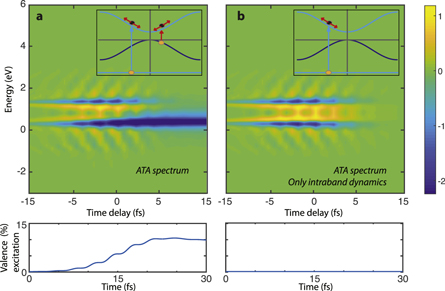
The corresponding ATA spectrum is shown in figure 3(a). The colormap has been normalized, with yellow and blue indicating the increase and decrease of absorption in comparison with the IR laser is not present. The ATA shows a complex structure, in which carriers are promoted both from the valence and the core band into the conduction band. In figure 3(b) we show the results of an additional simulation, with the same parameters, in which the transitions between valence and conduction band have been artificially disconnected. Note that the IR field is still allowed to induce intraband transitions. In this case, we observe that the decrease of absorption corresponding to the lower edge of the conduction band has vanished. Interband transitions promote carriers from the valence to the conduction, mainly at the lower energies of the band, precluding then the possibility of core electrons to be excited due to Pauli blocking. At the bottom of figure 3(a) we depict the conduction excitation as a function of time that is in agreement with the time delays in which the decrease of absorption is observed at the bottom edge of the band.
Figure 3. Interband and intraband contributions on the transient absorption spectrum. On the top panel, transient absorption spectra, on the bottom panel, conduction excitation of the IR laser pulse, considering (a), the IR laser pulse induces both intraband and interband transitions, and (b), the IR laser pulse only induces intraband transitions. The yellow and blue colormap indicates the increase and decrease of absorption with the IR laser pulse respectively.
Download figure:
Standard image High-resolution imageThe comparison of figures 3(a) and (b) also shows that the complex structure of the absorption enhancement (yellow areas) is not affected by the interband transitions from the valence band, therefore can be attributed to the intraband dynamics. Note that in previous studies of attosecond excitations from valence bands to high conduction bands [5], intraband interactions arisen from the IR field also modify the attosecond absorption spectrum, similarly to our observations. In the following section we develop a semiclassical approach in order to understand this structure and its dependence on the laser-driven intraband dynamics.
3.1. Semiclassical approach
By exploiting the correspondence between the SBE and the TD-CIS approach introduced in a previous section, we develop a simple two-band model to describe the main features of the laser-driven intraband dynamics. We restrict our dynamics to the evolving state
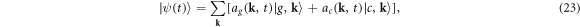
where  stands for the ground state, while
stands for the ground state, while  is the excited state formed by the core electron promoted into the conduction band. The amplitudes are found to obey the EOMs
is the excited state formed by the core electron promoted into the conduction band. The amplitudes are found to obey the EOMs
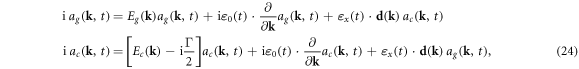
where Eg (k) and Eg (k) are the energies for the ground and excited state,  and
and  the electric field of the laser and x-ray pulse, d (k) the electric dipole transition, and Γ is the core-hole decay. We consider that the attosecond x-ray pulse excites a small fraction of the system in a very short time, i.e. the system is suddenly excited. Within the sudden approximation, the second line of equation (24) gives rise to the solution
the electric field of the laser and x-ray pulse, d (k) the electric dipole transition, and Γ is the core-hole decay. We consider that the attosecond x-ray pulse excites a small fraction of the system in a very short time, i.e. the system is suddenly excited. Within the sudden approximation, the second line of equation (24) gives rise to the solution
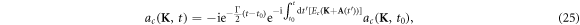
where we use the Volkov transformation,  , as it is usual in strong-field theory [38], where A(t) is the vector potential of the laser pulse and ac (K, t0) is the small fraction of excited state produced by the attosecond pulse, considered as an impulse at t0. Now that we have an analytical expression for the amplitudes as a function of time, we calculate the dipole response of the system (11) that is proportional to the absorption (14). The dipole evolution of the system, in the Volkov picture, is given by
, as it is usual in strong-field theory [38], where A(t) is the vector potential of the laser pulse and ac (K, t0) is the small fraction of excited state produced by the attosecond pulse, considered as an impulse at t0. Now that we have an analytical expression for the amplitudes as a function of time, we calculate the dipole response of the system (11) that is proportional to the absorption (14). The dipole evolution of the system, in the Volkov picture, is given by
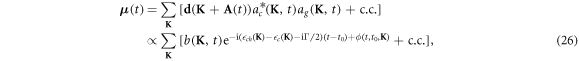
where the energy difference of the transition is given by the energy difference of the core-hole and the conduction band  , b(K, t) is a slow-variant function in time, and the phase
, b(K, t) is a slow-variant function in time, and the phase  is, using that the core-hole energy band has a small dependence with the quasi-momentum k
is, using that the core-hole energy band has a small dependence with the quasi-momentum k
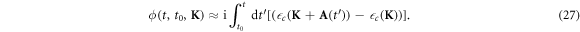
If there is not laser pulse, the dipole response (26) has an oscillating term, given by the energy difference of the transition, that is damped by the Γ factor. By the presence of the laser pulse, the oscillating term acquires a phase (27) that depends in a trajectory in the reciprocal space driven along the polarization of the electric field. Depending on the position in the reciprocal space, the acquired phase is different, this gives rise to the complex ATA interference structure shown in figure 3(b). Note that in the limit of a core-hole lifetime much larger than the IR laser pulse, and when attosecond excitations only involve transitions around the gamma point, we will recover the absorption formula found in a two-band parabolic model [39].
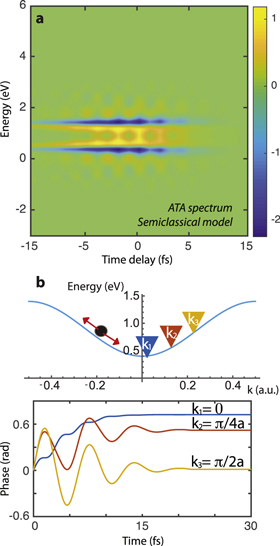
We use our model to calculate the absorption of the system by using the following approach: (i) at different positions in the reciprocal space, we consider a trajectory driven by the vector potential of the laser field, (ii) for each trajectory, we calculate the phase (27) that depends on the energy band wandered by the carrier, (iii) we calculate the dipole response (26) by summing all trajectories, taking into account the energy of the transition and the phase at each position of the reciprocal space. By using this semiclassical model, we obtain the ATA spectrum shown in figure 4(a), in very good agreement with figure 3(b). This model also provides a simple interpretation of the main features. At the gamma point k = 0, the electron driven by the laser pulse can only move to higher energies, and the accumulated phase (27) for any trajectory is positive, see figure 4(b). This is quite different for a position at the middle of the band, such as at k = ±π/2a, where the laser-driven electron could go to positive and negative energies, and the accumulated phase could be positive or negative and more sensitive to the initial excitation, i.e. time delay between the laser and the attosecond pulse. Also, a 2ω0 structure, being ω0 the frequency of the laser pulse, is clearly observed at the middle of the band, as it is expected by the accumulated phase at symmetric points such as k = ±π/2a. At further points k = ±π/a, the accumulated phase only is negative, opposite to the behavior found at gamma point. In conclusion, the coherent phase accumulated by the carriers driven along the reciprocal space determines the spectral features in the attosecond absorption spectrum. Interestingly, the ATA features arisen from intraband dynamics contain the information of the energy bands. Note that this model assumes that the excitation is shorter than the period of the laser pulse and the decoherence or decay times. If the excitation is comparable to the period of the electric field, the coherent superimposed signal would be blurred in the absorption spectrum. Also, one expects that electron-hole interactions would play a role and modify the spectrum. This shows the potential of this unique approach to access ultrafast electron dynamics and obtain electronic properties of condensed-matter systems.
Figure 4. Intraband effects derived from a semiclassical model. (a), Transient absorption spectrum calculated from a semiclassical model, see text for more details. (b), Coherent accumulated phase for different positions at the reciprocal space for zero time delay.
Download figure:
Standard image High-resolution image3.2. Fano profiles from laser-induced intraband dynamics
In early experiments of attosecond transient spectroscopy, by studying Fano resonances in atomic systems, it was shown that the ultrashort IR laser has an important effect on the lineshape of the absorption spectrum [28]. In those experiments, an autoionizing state was excited with an XUV attosecond pulse. After excitation, and during the autoionization decay lifetime, a few-cycle IR pulse was sent to the atomic system to induce a dynamical Stark shift. This energy shift results in a phase change in the time-dependent dipole response of the system, giving rise to a change in the absorption lineshape.
Here we show that the intraband dynamics results in Fano lineshapes in the ATA spectrum similar to the effects found in atomic systems.
In the reciprocal space, the absorption at a particular quasi momentum is linked to the transition from the ground state to the core-hole state, i.e. the created pair electron and core hole at a particular k. During the subsequent decay of the electron-core-hole pair, the energy of the exciton is modified by the quiver induced by the laser, introducing then a complex dynamical Stark shift. The excursion of the electron introduces a quantum phase in the probability amplitudes, that is translated to a dephase in the dipole response, see equation (26) and the discussion in the previous section. Depending on the initial position in the reciprocal space, the induced phase shift is different because of the local energy dispersion.
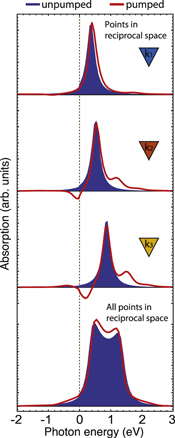
Figure 5 shows, for the same positions shown in figure 4(b), the absorption lineshape changes induced by the laser pulse. When the laser is not present, blue filled lines in 5, we observe the expected Lorentzian lineshape for the three different positions in the reciprocal space. However, the presence of the laser puse, in this case synchronized at time delay zero with the attosecond x-ray pulse, modifies the lineshape and it depends on the reciprocal-space position. At k1, the main change is due to an energy shift, while for k2 and k3 we observe substantial changes in the lineshape profile, similar to the observed laser-induced Fano lineshapes in atomic systems.
Figure 5. Laser-induced Fano lineshapes. Absorption spectrum calculated at three different positions, shown in figure 4(b), of the reciprocal space with (red line) and with no (blue filled line) laser pulse. For comparison, we show the total absorption spectrum, given by summing the contribution of all the points in the reciprocal space. These calculations correspond to a time delay zero.
Download figure:
Standard image High-resolution image4. Conclusion
In conclusion, being able to investigate the lightwave electron motion in the attosecond timescale is a new frontier that opens promising venues to both fundamental condensed-matter physics and applications in material science. Knowing the position of electrons in real time is essential to boost the design of rational materials with specific functionality. This goal is now achievable with attosecond x-ray transient absorption spectroscopy, an ultrafast technique developed with HHG sources. The advance of this unique technology needs also the development of time-dependent theoretical approaches to interpret and understand experimental measurements. We show that SBE may be reformulated in order to separate the two different dynamics induced by the IR pump and the attosecond x-ray probe pulse, mainly involving electrons close to the Fermi levels and electrons close to the nuclei, respectively. Within this theoretical formalism, we easily distinguish intraband and interband dynamics, this facilitates the track of the underlying mechanism and the construction of simpler analytical models. The access to sub-femtosecond dynamics, and the lightwave behavior of electrons, make coherent effects to play an important role in the calculated observables. This is the case of the electron transport signature on the x-ray absorption spectrum induced by the intraband interactions with the laser pulse. Here, we study the main features of this effect by using a three-band system that allows us to develop a simple semiclassical model. Interestingly, these intraband effects depend on the local energy band structure around the k-space excitation and can be connected with previous works on light-induced Fano resonances in atomic systems. Because this scheme involves transitions from core bands, the reported intraband effects are dominated by the energy dispersion of the bands close to the Fermi level.
This work opens the door to explore the possibility of performing tomography of complex energy bands [40], to detect coherent effects in light-field-driven currents [41, 42], to study nonadiabatic dynamics in graphene during high-harmonic generation [43], and to investigate topological and valleytronics properties in two-dimensional materials [44].
Acknowledgments
This project has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie Grant Agreement No. 702565 as well as from Comunidad de Madrid through the TALENTO program with ref. 2017-T1/IND-5432. LP acknowledges support from Junta de Castilla y León (Project SA046U16) and MINECO (FIS2016-75652-P). JB acknowledges financial support from the Spanish Ministry of Economy and Competitiveness (MINECO), through the Severo Ochoa Programme for Centres of Excellence in R&D (SEV- 2015-0522) Fundació Cellex Barcelona and the CERCA Programme / Generalitat de Catalunya, the European Research Council for ERC Advanced Grant TRANSFORMER (788218), MINECO for Plan Nacional FIS2017-89536-P; AGAUR for 2017 SGR 1639 and Laserlab-Europe (EU-H2020 654148).
Author contributions
AP and JB conceived the idea. AP developed the theoretical model with contributions from LP AP, JB, and LP discussed the results and wrote the manuscript.
Competing financial interests: The authors declare no competing financial interests.