Gravitation in the Fractal D = 2 Inertial Universe: New Phenomenology in Spiral Discs and a Theoretical Basis for MOND

Abstract

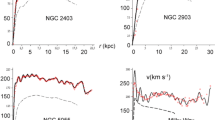
A particular interpretation of Mach's Principle led us to ask if it was possible to have a globally inertial universe that was irreducibly associated with a non-trivial global matter distribution, Roscoe [1]. This question received a positive answer, subject to the condition that the global matter distribution is necessarily fractal, D = 2. The present paper shows how gravitational processes can arise in this universe. We begin by showing how classical Newtonian gravitation arises from point-source perturbations of this D = 2 inertial background. We then use the insights gained from this initial analysis to arrive at a general theory for arbitrary material distributions. We illustrate the process by using it to model an idealized spiral galaxy. One particular subclass of solutions, (the logarithmic spiral) has already been extensively tested (Roscoe [2, 3]), and shown to resolve large samples of optical rotation curve data to a very high statistical precision. These analyses also led to the discovery of a major new phenomenology in spiral discs—that of discrete dynamical classes, [3]. In this paper, we analyse the theory more comprehensively, showing how this phenomenology has a possible explanation in terms of an algebraic consistency condition which must necessarily be satisfied.

Of equal significance, we apply the theory with complete success to the detailed modelling of eight Low Surface Brightness spirals (LSBs) which, hitherto, have been successfully modelled only by the MOND algorithm (Milgrom [5–7]. We are able to conclude that the essence of the MOND algorithm must be contained within the presented theory.