Introduction

Inland waters are more important in the global carbon (C) cycle than generally perceived; they serve a dual role by sequestering C for burial in sediments while serving as conduits of the greenhouse gases (GHGs) CO2, CH4 and N2O to the atmosphere (Bastviken et al. 2004a; Cole et al. 1994; Hessen et al. 1990; Tranvik et al. 2009; Yang et al. 2008). Most effort has been devoted to the CO2 production in lakes, and in general lakes are net heterotrophic being strongly supersaturated with CO2 (Cole et al. 1994; Kling et al. 1992). This holds particularly for lakes with high concentrations of dissolved organic matter (DOM) or total organic carbon (TOC) (Jansson et al. 2007; Larsen et al. 2011a; Sobek et al. 2007). Kortelainen et al. (2013) found a C evasion to accumulation ratio ranging from 4 to 86 (average 30) in TOC rich lakes. Such lakes dominate the boreal biome of the northern hemisphere and typically are important conduits of GHGs. This is mostly because in-lake metabolic processes by heterotrophic bacteria and methanogenic archaea convert allochthonous organic matter to CO2 and CH4 (Bastviken et al. 2004b). Generally, these small lakes show disproportionately high emissions per surface area owing to their high concentrations of TOC and anoxic deep-waters (Bastviken et al. 2004a).

A number of studies have addressed the major determinants of CO2 and CH4 concentrations and export in and from lakes, and found lake productivity to be the major driver, ultimately controlled by phosphorus (P) content, TOC concentration and lake morphometry (Juutinen et al. 2009; Yang et al. 2011). High nutrient levels promote autochthonous primary production which provides substrate for methanotrophs (Huttunen et al. 2003a; Schwarz et al. 2008; West et al. 2012). High primary production also increases the hypolimnetic respiration and sediment anoxia that may result in elevated emissions of CO2 and CH4. Alternatively, inputs of inorganic C linked to catchment properties may play a major role in CO2 release (Kankaala et al. 2013; McDonald et al. 2013).

Lakes may also be a net-source for N2O, but there are few estimates for N2O dynamics in boreal regions. As an intermediate of denitrification, N2O should a priori be expected to depend on organic carbon, oxygen availability, temperature and nitrate concentration, which were shown to be the major predictors of N2O in previous surveys of temperate lakes (Huttunen et al. 2003b; Kortelainen et al. 2013; Liikanen et al. 2003; Tremblay et al. 2005), pointing to elevated N deposition and warming as future drivers for N2O-emissions from boreal lakes.

Concentrations and fluxes of CO2, CH4 and N2O in lakes are dynamic and vary with depth and season (Casper et al. 2000; Huttunen et al. 2003a; Riera et al. 1999; Xing et al. 2005). The major drivers of gas dynamics are related to metabolic processing of organic material, and subsequent solubility and gas diffusion.

Boreal lakes often have high area-specific GHG emissions (e.g. Bastviken et al. 2011; Raymond et al. 2013). Lake metabolism and hence the concentrations of CO2, CH4 and N2O, their seasonal dynamics and emission are primarily influenced by lake morphometry and parameters governing primary and secondary productivity (e.g. Huttunen et al. 2003a; Juutinen et al. 2009; Larmola et al. 2004). Typically, concentrations of total P (TP) regulate the primary productivity, while allochthonous input of TOC stimulates production and respiration of heterotrophic bacteria (Berggren et al. 2009). The role of colored TOC is at least twofold, since it not only fuels productivity of heterotrophic bacteria, but also reduces primary production to due light attenuation (Jones et al. 2012; Seekell et al. 2015; Thrane et al. 2014). Dissolved organic matter, of which TOC constitutes a major pool, may however also be a source of TP and total N (TN) in pristine, boreal lakes (Kortelainen et al. 2006a). Both high autotrophic and heterotrophic productivity may generate hypolimnetic oxygen deficits or anoxia, thereby strongly affecting the gas concentrations and emissions (Hessen and Nygaard 1992; Huttunen et al. 2003a; Juutinen et al. 2009; Larmola et al. 2004). Hence, the net effect of autotrophic and heterotrophic productivity, or the role of TOC versus TP, on gas concentrations and emissions are not always straightforward.

Most studies in boreal lakes have addressed one or two GHGs (e.g. Demarty et al. 2011; Kankaala et al. 2013; Kortelainen et al. 2006b; Lemon and Lemon 1981; Ojala et al. 2011; Tremblay et al. 2005) (Table 1), while studies addressing all three biogenic GHGs (CO2, CH4, N2O) are very limited (Huttunen et al. 2003a; Tremblay et al. 2005).

Table 1 Comparison of greenhouse gas fluxes in boreal lakes
Full size table

To reveal the major drivers of concentrations and emissions of these gases, we measured epilimnetic concentrations of CO2, CH4, N2O, N2, O2 and Argon (Ar) in a synoptic survey covering 75 dimictic, boreal lakes in Norway and Sweden, with surface areas >1 km2 and low to intermediate productivity. Exchange fluxes at the interface between water and atmosphere of Ar are controlled mainly by advection and turbulent mixing. Ar can thus serve as an inert tracer of these processes (Schwarzenbach et al. 2005; Tomonaga et al. 2012), and many studies report close agreement of dissolved Ar in water and expected atmospheric equilibrium concentration (e.g. Aeschbach-Hertig et al. 1999; Craig et al. 1992; Peeters et al. 1997; Tomonaga et al. 2012; Wilkinson et al. 2015). On the contrary, O2 and the GHGs CO2, CH4 and N2O are also affected by biogeochemical processes, for example photosynthesis, respiration, methanogenesis, methanotrophy, nitrification, and denitrification (e.g. Schwarzenbach et al. 2005). Ar, being biologically inert, may thus serve as an ideal tool for normalizing concentrations of other gases, yet it has so far rarely been applied in limnological studies (Craig et al. 1992; Tomonaga et al. 2012; Wilkinson et al. 2015). In this study, we make the first attempt to calculate Ar-normalized gas saturation for O2, CO2, N2O and CH4 and use the relative deviation from Ar-equilibrium at a late summer sampling as a proxy for cumulative net metabolic activity since spring overturn in boreal lakes. In addition, we estimated the GWP of these three GHGs, CO2, CH4 and N2O in CO2 equivalents and analysed the effect of lake productivity, browning and other factors on the GWP of boreal lakes.

Materials and methods

Sampling programme

The sampled lakes spanned a wide range of physical, chemical and biological properties, but were primarily selected to span wide and orthogonal gradients in TOC and total phosphorus (TP). Existing data of the Norwegian and Swedish lake monitoring scheme (Solheim et al. 2008) and of the Northern European lake survey (Henriksen et al. 1998) were combined to generate a subset of lakes satisfying the following criteria: latitude 57–64°N, altitude <600 m, surface area >1 km2, pH > 5, TP < 30 µg L−1, and TOC < 30 mg L−1. 75 lakes were chosen from this subset by stratified randomization to ensure best possible coverage and orthogonality with respect to concentrations of TOC and TP (Fig. 1). The lakes were sampled by hydroplane during July and August 2011.

Fig. 1
figure 1

Location and total organic carbon (TOC) concentration of the surveyed lakes in Norway and Sweden

Full size image

Composite samples (15 L in total) from 0 to 5 m were taken with an integrating water sampler (Hydro-BIOS, Germany) in the central part of each lake during daytime. Water temperature was measured using XRX-620 10-channel CTD (RBR Ltd., Canada). High-resolution vertical temperature profiles indicated that the thermocline was deeper than 5 m in all lakes (Fig. 2), and that, accordingly, the integrated 0–5 m samples could be considered representative of the entire mixed layers of the lakes. Water transparency was measured by lowering a white Secchi disc and recording the depth where it was no longer visible.

Fig. 2
figure 2

Temperature profiles in summer in the surveyed lakes in Norway and Sweden

Full size image

Chemical analysis

Concentrations of TP, TN and TOC were measured both at the accredited laboratories at the Norwegian Institute for Water Research (NIVA) and at the University of Oslo (UiO). TP was measured on an auto-analyzer as phosphate after wet oxidation with peroxodisulfate in both laboratories. TN was measured by detecting nitrogen monoxide by chemiluminescence using a TNM-1 unit attached to the Shimadzu TOC-VWP analyzer (UiO), or detection of nitrate after wet oxidation with peroxodisulfate in a segmented flow autoanalyzer (NIVA). Since the results from the two laboratories were very similar, results were averaged for the following analysis.

Gas analysis and Ar-normalization

Water from the integrated water sample (same depth interval as for the other parameters) was gently let into 120 mL glass serum-vials without bubbling, fixed with 0.2 % HgCl2 and sealed with gas-tight butyl rubber stoppers. The samples were stored cold (4 °C) in the dark prior to analysis. Concentrations of Ar, O2, N2, N2O, CO2 and CH4 were determined by headspace technique. For this, bottles were allowed to reach room temperature before backfilling them with 20–30 mL Helium (He) while removing a corresponding volume of water from the bottle. The bottles were shaken horizontally at 150 rpm for 2 h to equilibrate gases between sample and headspace. The temperature during shaking was recorded by a data logger. Immediately after shaking, the bottles were placed in an autosampler (GC-Pal, CTC, Switzerland) coupled to a gas chromatograph (GC) with He back-flushing (Model 7890A, Agilent, Santa Clara, CA, US). Headspace gas was sampled (app. 2 mL) by a hypodermic needle connected to a peristaltic pump (Gilson Minipuls 3), which connected the autosampler with the 250 µL heated sampling loop of the GC.

The GC was equipped with two separation lines: a 20 m wide-bore (0.53 mm) Poraplot Q column for separation of CH4, CO2 and N2O from bulk gases and a 60 m wide-bore Molsieve 5Å PLOT column for separation of Ar, O2 and N2. Both columns were run at 38 °C with He as carrier gas. Even though samples could be run simultaneously on both lines using a time controlled column isolation valve switching the Molsieve column in and out of the analyte stream, we found that switching this valve contaminated the sample with >10 % ambient Ar. We therefore analyzed the samples for CH4, CO2 and N2O first and then analyzed Ar, O2 and N2 in a second run. To avoid pressure drop in the bottles between the runs, an equivalent amount of He was automatically pumped back from a He line located at the waste end of the GC by reversing the peristaltic pump, thereby diluting the headspace (for details, see Molstad et al. 2007).

N2O was measured on an electron capture detector run at 375 °C with 17 mL min−1 Ar:CH4 (90:10 vol%) as makeup gas. CH4 was analyzed by a flame ionization detector, while all other gases were measured by a thermal conductivity detector (TCD). Certified standards of CO2, N2O and CH4 in He were used for calibration (AGA, Germany), whereas N2, O2, and Ar were calibrated against air. The analytical precision for all gases was better than 1 %. Relative headspace concentrations (corrected for dilution in the second run) were used to calculate the concentrations of the dissolved gases in the samples using temperature-dependent Henry’s law constants provided by Wilhelm et al (1977) and the average temperature recorded during the 2 h equilibration period.

O2 was measured independently using XRX-620 CTD equipped with a Rinko III fluorometric oxygen probe at <5 cm vertical resolution and averaged over the same depth interval as the integrated water samples. The results correlated closely with those obtained from GC (r2 = 0.63, p < 0.001).

Dissolved gas concentrations in dimictic lakes in summer may be seen as the net result of all metabolically and physically driven changes since the (possibly incomplete) circulation at spring overturn. We thus calculated saturations relative to atmospheric equilibrium for all gases using in situ measurement of water temperature. Henry’s law constants (taken from Wilhelm et al. 1977) were recalculated from 25 °C to in situ water temperature using the Clausius–Clapeyron equation with gas-specific enthalpies of solution given by Wilhelm et al (1977). Equilibrium concentrations were then calculated as Henry’s law constants multiplied by average atmospheric pressures of individual gases.

Ar in water is governed solely by physical processes such as diffusion and partition between different phases, while O2, N2 and the GHGs CO2, CH4 and N2O are controlled by both physical and biogeochemical processes (Aeschbach-Hertig et al. 1999). We thus used the relative saturation of this noble gas to normalize the relative saturations of all other gases. This normalization corrects for incomplete atmospheric equilibration at spring overturn.

GHG fluxes

We calculated the greenhouse gas (GHG) partial pressures (pCO2, pCH4, pN2O), and thereby estimated the flux using water temperatures and wind speeds. The mass transfer coefficient was estimated from local wind speed provided by the Norwegian Reanalysis Archive, a dynamical downscaling of ERA-40 (references are given in the Supplementary Material), and the Schmidt number (Cole and Caraco 1998; Johnson 2010; Wanninkhof 1992). Partial pressures were calculated from GHG concentration in the water and their Henry’s law constants (Wanninkhof 1992), temperature adjusted according to Wilhelm et al. (1977). CO2, CH4 and N2O fluxes were then calculated as the product of the gas saturation deficit (difference between partial pressures) and the Schmidt number. It is noteworthy that the Schmidt number calculated by the method provided by Cole and Caraco (1998) gives a theoretical value, which may result in an underestimation of actual emissions because wind speeds at low convective mixing may play an important role (Read et al. 2012) . For more details see equations in Supporting Information.

Global warming potentials (GWP, time horizon 100 year) for aggregate GHGs CO2, CH4, and N2O release from lake surfaces were calculated as CO2 mass equivalents using the latest IPCC report coefficients of 34 for CH4 and 298 for N2O (Myhre et al. 2013).

An array of correlation analyses was conducted for GHG (CO2, CH4, and N2O) concentrations, Ar normalized saturation and GWP with environmental variables in these lakes. As environmental variables we included lake altitude, lake area, lake depth at sampling point (a proxy for maximum depth), chlorophyll a (Chl a), total organic carbon (TOC), total inorganic carbon (TIC), total phosphorus (TP), total nitrogen (TN), NO3 −, Secchi depth, and area-specific primary production (PPA). In brief, the PPA estimates were calculated using a bio-optical model based on phytoplankton absorption, in situ irradiance, and the light dependent quantum yield of photosystem II. See Thrane et al. (2014) for details. All the statistical analyses were conducted using the software R (R Core Team 2014).

Results

Across all lakes, the mean surface molar concentrations of N2 and O2 were 577.5 and 285.6 µmol L−1, while average concentrations of CO2, CH4 and N2O were smaller with 47.0, 0.13 and 0.015 µmol L−1, respectively (Fig. 3). The mean concentration of Ar was 16.0 µmol L−1. Concentrations of gases, particularly those of the GHGs, ranged widely across all lakes. Inert Ar and semi-inert N2 showed a relative smaller variability [coefficients of variation (CV) = 6.3 and 7.3 %], while the variability was greater for O2 and N2O (CV = 11.7 and 30.4 %), and highest for CO2 and CH4 (CV = 63.0 and 100.5 %). The Ar-corrected gas saturations increased from O2 (mean = 85.5 %, CV = 8.2 %) and N2 (mean = 94.1 %, CV = 2.2 %) to N2O (mean = 147.0 %, CV = 29.1 %), CO2 (mean = 272.1 %, CV = 63.1) and CH4 (mean = 4263 %, CV = 106.5 %) (Fig. 3). Variations in GHG saturation among these lakes were much larger than those of N2 and O2.

Fig. 3
figure 3

Epilimnetic gas concentration (a) and Ar normalized gas saturation (b) of the surveyed lakes in Norway and Sweden. Y axis is a 10-base logarithmic scale. The values are the means of gas concentrations or saturation in %

Full size image

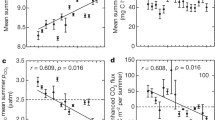
Surface CO2 concentrations across lakes were significantly negatively correlated with surface O2 concentration (r2 = 0.232, p < 0.0001, Fig. 4c). The slope of the CO2/O2 deficit relationship (mean ± SD, 1.039 ± 0.630) indicated that CO2 was produced at unit stoichiometry [respiratory quotient (RQ) = 1] with O2 consumption by biological or photochemical oxidation of organic matter (Fig. 4d).

Fig. 4
figure 4

Gas concentration in the surveyed lakes in Norway and Sweden. a Ar and N2 concentration, the dash line is saturation level; b Ar and CO2 concentration, the dash line is saturation level; c Negative correlation between O2 and CO2 concentration (r2 = 0.24, p < 0.001), the solid line is the best-fit line; d Positive correlation between Ar-based O2 deficit and CO2 concentration (r2 = 0.57, p < 0.001), the dash line is 1:1 ratio, indicating that 1 mol O2 was consumed to produce 1 mol CO2. Unit of gas concentration is µmol L−1

Full size image

Secchi depths across lakes was negatively correlated with TOC (r2 = 0.528, p < 0.0001), less so with Chl a (r2 = 0.164, p < 0.01), yet these two parameters combined explained >60 % of Secchi depth variability arguing for keeping this variable in the analysis.

Using a range of the lake-specific parameters as explanatory variables (see “Materials and methods” section), we were able to explain 42–79 % of the variance in surface gas concentrations, with the highest degree of explanation for CO2 concentrations and the lowest for CH4 concentrations (Table 2). The major explanatory variables for surface CO2 concentrations were TOC (r2 = 0.221, p < 0.001) and TP (r2 = 0.117, p < 0.01). Surface CH4 concentrations were best explained by Chl a (r2 = 0.304, p < 0.0001), TP (r2 = 0.234, p < 0.0001), total inorganic carbon (TIC) (r2 = 0.169, p < 0.01) and conductivity (r2 = 0.124, p < 0.01). For surface N2O concentrations, unsurprisingly TN (r2 = 0.250, p < 0.0001) and NO3 − (r2 = 0.299, p < 0.0001) were the main explanatory variables, accompanied by TP (r2 = 0.301, p < 0.0001), Chl a (r2 = 0.120, p < 0.01) and area-specific primary production (PPA) (r2 = 0.142, p < 0.001). Interestingly, PPA did not appear as a major determinant for surface CO2 concentrations (r2 = 0.003, p = 0.633) or for O2 concentrations (r2 = 0.018, p = 0.249).

Table 2 Correlation between greenhouse gas (CO2, CH4, and N2O) concentration, Ar normalized greenhouse gas saturation and global warming potential (GWP) with environmental variables in the surveyed lakes in Norway and Sweden
Full size table

Lake morphometry and physical properties had no significant impact on GHG concentrations. For example, lake area (r2 = 0.063, p = 0.023), depth (r2 = 0.061, p = 0.011) and altitude (r2 = 0.019, p = 0.188) had little impact, yet depth gave a weak negative contribution to surface CH4 concentration. Likewise, temperature appeared as a minor contributor (r2 = 0.020, p = 0.258).

The average flux of CO2 was 20.48 mmol m−2 day−1 with a range of −10.75 to 82.16 mmol m−2 day−1 (Table 1). The average fluxes of CH4 and N2O were smaller, 2.32 mmol m−2 day−1 (range 0.11–15.01) and 4.76 µmol m−2 day−1 (range 1.85–38.00), respectively. The average GWP for all lakes was 50.71 mmol m−2 day−1 with a range of 6.39–207.85 mmol m−2 day−1 (Fig. 5).

Fig. 5
figure 5

Greenhouse gas fluxes from different types of the surveyed lakes in Norway and Sweden. a and b are CO2; c and d are CH4; e and f are N2O; g and h are the global warming potential (GWP). Lakes were divided into groups: small area (<10 km2) and large area (>10 km2); low TOC (<average 6.25 mg L−1) and high TOC (>6.25 mg L−1) divided by the mean concentration of TOC; oligotrophic (4–10 µg L−1 TP) and mesotrophic (10–35 µg L−1 TP) following OECD 1982. To compare greenhouse gas concentrations and emissions, the lakes were divided to groups according to area, TOC concentration and eutrophic levels. Lakes were divided to small (1–10 km2) and big (10–100 km2) lakes. The mean concentration of TOC was used as threshold to divide the lakes to two groups. Following the OECD classification of trophic state (OECD 1982), lakes were divided to oligotrophic (TP 4–10 µg L−1) and mesotrophic (TP 10–35 µg L−1) groups

Full size image

Unsurprisingly, despite the different wind fetches of the sampled lakes, the calculated emissions for CH4, CO2 and N2O (Fig. 5) closely matched the epilimnetic gas concentrations (r2 > 0.85, p < 0.001). Gas emissions have largely the same explanatory variables as gas concentrations.

GWP of these three GHGs across the lakes was best explained by TP (r2 = 0.340, p < 0.0001), Chl a (r2 = 0.202, p < 0.001), TOC (r2 = 0.187, p < 0.001), followed by depth (r2 = 0.109, p < 0.01) and TN (r2 = 0.104, p < 0.01).

The spatial variation of GHG fluxes across the 75 lakes is shown in Fig. 5. When grouping the lakes in each two categories of size (area), TOC and TP, emissions of all measured GHGs and consequently also GWP were consistently higher in small lakes and lakes with high levels of TP and TOC.

Discussion

In this survey, very small lakes were avoided and sites were deliberately chosen to yield orthogonality of TOC and TP for estimating GHG emissions from lakes. Wind speed during the research period in the 75 lakes was below 5 m s−1 (see Supporting Information), therefore bubble injection, one of the possible factors influencing the gas exchange in the water-air interface, was considered negligible (Craig and Hayward 1987) and the use of the Cole and Caraco (1998) emission model was justified. This should minimize the role of confounding factors related to size and shape of lakes, and allow for more robust assessments of TOC and nutrients as drivers of GHG production and emissions. Furthermore, Ar-normalized saturation deficit/excess was used to assess the net metabolic changes since spring overturn.

We found that lakes with higher nutrient levels in general had higher emissions of CO2 and CH4 in accordance with Huttunen et al (2003a). Although Kankaala et al. (2013) did not report clear difference in CO2 flux between small lakes (1–10 km2) and large Finnish lakes (10–50 km2), their study showed that the smaller lakes (<1 km2) emitted more CH4 than larger (1–10 km2) lakes (Table 1). Other studies have reported higher emissions of both CO2 and CH4 in smaller lakes (Kortelainen et al. 2006b). Due to the low number of published data, it is difficult to compare N2O flux across the lakes with different sizes, nutrient levels, and TOC concentrations. While lake morphometry may be important (Huttunen et al. 2003b; Wang et al. 2006), our study clearly pointed to nutrient concentrations, and notably N as a major driver. This is in support of studies pointing to elevated N deposition as a major driver of N2O emissions also from lakes (Kortelainen et al. 2013; McCrackin and Elser 2010).

Concentrations and Ar-normalized saturation for the various gases responded to the same parameters (Table 2). In terms of the surface CO2 concentrations, TOC was the main predictor, followed by TP. The degree of net heterotrophy, as reflected by O2 saturation deficit or CO2 super-saturation, was primarily related to TOC stimulating prokaryotic heterotroph activity while at the same time reducing autotrophic production due to light attenuation (slope of the CO2/Ar-based O2 deficit relationship was 1.039, Fig. 4d). Unsurprisingly, CO2 concentrations correlated negatively with lake pH (only free CO2 was measured). It is rather striking that CO2 correlated positively with TP, while TP had apparently no net impact on O2. TP may in this context play a dual role, both by promoting mineralization of TOC by heterotrophic bacteria and by promoting autotrophic production. Based on the relationship between TP and O2 (r2 = 0.042, p = 0.076), TP may stimulate heterotrophic bacteria more than autotrophic plankton. Also the poor correlation between area-specific primary production and CO2 as well as O2 suggests a major role of catabolic processes (Cole et al. 1994; Hessen et al. 1990), photo-oxidation (Cory et al. 2014; Koehler et al. 2014), or inputs of exogenous CO2, such as from groundwater (Öquist et al. 2009).

Surface CH4 concentrations across lakes were mainly governed by TP and Chl a, suggesting the importance of lake productivity for the CH4 concentrations. TP is the nutrient which usually limits the primary production in oligotrophic and mesotrophic boreal lakes (e.g. Nurnberg and Shaw 1998). High phytoplankton production can supply bioavailable organic matter to the sediment, thus supporting methanogenesis and production of CH4. Studies found that the fresh organic C from primary production and flooded previous biomass has a greater contribution than old peat deposits to CH4 production in some boreal waters (Huttunen et al. 2002; Kelly et al. 1997).

Similar as with CH4 concentrations, surface N2O concentrations were best explained by TP and Chl a, indicating importance of autotroph production for these gases. Also, nitrogen (total N and NO3 −) was a strong contributor to N2O. TN is partly on organic form as DOM, while NO3 − is closely related to atmospheric N deposition in these pristine lakes (Hessen et al. 2009).

The key roles of lake morphometry and catchment properties for GHG concentrations and emissions have been verified for several boreal lakes (Kankaala et al. 2013; Read et al. 2012). It is noteworthy that neither of the physical properties including altitude, area and depth of the lakes were major determinants of the GHG concentrations and fluxes, despite a trend for higher production and emission in smaller lakes. This likely reflects the fact that very small and sheltered lakes were avoided in this study, and hence that geographical and morphological variability was minor relative to the gradients in TOC and TP.

TOC concentration typically reflect the proportion of forest, bogs and wetlands within the catchment, and is generally one of the main sources of dissolved CO2 (Humborg et al. 2010; Kortelainen 1993; Larsen et al. 2011b; Larsen et al. 2011c; Sobek et al. 2003). This is partly attributed to bacterial mineralization (del Giorgio and Peters 1994; Hessen et al. 1990) or photo-oxidation (Cory et al. 2014; Koehler et al. 2014), both processes typically generating supersaturation in boreal lakes and thus net release of CO2 (Cole et al. 1994). Inputs of exogenous CO2 (i.e. from groundwater) could also contribute substantially to CO2 in the water column (Humborg et al. 2010; Öquist et al. 2009) and also be one of the causes for decoupling between CO2 and O2 concentrations. Most studies identified TOC also as a major driver of dissolved CH4, yet often lake productivity, lake area, water column stability or ionic strength serve as key predictors (Hessen and Nygaard 1992; Juutinen et al. 2009; Kankaala et al. 2013; Sobek et al. 2003; Xing et al. 2006). In fact, for lakes in general, productivity and deep-water anoxia seem most important, while TOC is more important for CO2 concentrations and fluxes in small and sheltered lakes.

A key issue in boreal areas is how the observed increase in terrestrially derived DOM (i.e. lake “browning”), either being caused by reduced SO4-deposition (Monteith et al. 2007) on a decadal scale or by long term changes in vegetation density (Larsen et al. 2011a), will affect lake productivity and hence GHG concentrations and emissions. While browning doubtlessly will increase concentrations and fluxes of CO2, the net effect on CH4 is less clear. In boreal, pristine lakes, terrestrially derived DOM is the key source of TOC, as well as of P and N. TOC will decrease primary production owing to increased light attenuation (Thrane et al. 2014), but increase the likelihood of epilimnetic anoxia and thus support methanogenic activity (Bastviken et al. 2004a), hence the net effect of browning on CH4 is likely positive. For N2O, it is first and foremost high (or elevated) levels of N inputs that will promote increased emissions, and given the widespread impacts of increased N deposition on lake ecosystems (Elser et al. 2009; McCrackin and Elser 2011), the coupling of climate, TOC and N deposition for GHG-emissions is a topic that warrants further attention. Advancing our understanding of lake browning in terms of global warming (GWP, i.e. the combined effect of CO2, CH4 and N2O) is challenging but adds a new perspective to limnetic responses to future climate change. The highly significant correlation between TOC and GWP in our study suggests that the GWP will very likely increase with water browning in boreal area.

The current study is based on a single integrated sample from a large number of remote lakes, sampled by hydroplane. Due to diurnal and seasonal variation of gas flux (e.g. Natchimuthu et al. 2014; Xing et al. 2004), the scope of this study was not to calculate the annual flux of GHG (which then would have been achievable for a limited number of lakes only), but rather using Ar as the proxy for net metabolic changes from spring overturn to mid-summer, and their relationship to ambient parameters. Better insight in the drivers of both absolute and relative rates of change may serve an important input to models of future GHG emissions from boreal lakes.