Skip to main content
SpringerLink
Log in

Simulation of viscoelastic stagnation flow

  • Original Contributions
  • Published:
Rheologica Acta Aims and scope Submit manuscript

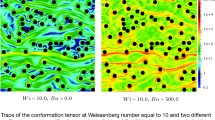
Abstract

A finite element simulation for the steady flow in a planar stagnation die was used to compute the velocity, pressure and stress fields. It is predicted that a region surrounds the stagnation point where the flow approximates a planar extension. This region is circular for the Newtonian liquid and becomes an ellipse for the Maxwell fluid. An isotropic point in the stress field is found for the Newtonian case as well as for the Maxwell fluid. Lubrication of the die wall, modeled as a finite slip, increases the size of extensional flow region by as much as 100%, while causing a migration of the isotropic stress point towards the die wall.

A slight increase in the apparent planar extensional viscosity occurs before the numerical scheme fails at deformation rates well below the extensional singularity in the Maxwell model. Slip at the walls does not significantly alter the convergence behavior, which appears to be limited by effects in the entry region. In this region, at a Weissenberg number of 1.16, spatial oscillations in the pressure, deformation rate and stress develop. The stress normal to the main flow direction in the entry region is compressive for all values of the slip coefficient.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

a :

Length of hyperbolic region in the stagnation die

A :

total area for flow in thexy-plane

C :

die constant;XY = C/h 2 at the die wall

da :

differential area element

ds :

differential contour length along the boundary

ϕ;A :

boundary of the flow

h :

half-width at die entry

I :

unit tensor

l i :

inlet length in the stagnation die

l o :

outlet length in the stagnation die

n :

unit outward normal to the boundary or to a streamline

n i :

unit outward normal to a finite element at the boundary

P :

pressure; normalized byηV/h

P i :

nodal value of pressure in an element

Q :

volumetric flow rate through the die

T :

total stress tensor; normalized byηV/h

t :

unit tangent to the boundary or to a streamline

t i :

unit tangent to a finite element at the boundary

V :

maximum speed at the centerline of inlet or outlet

v :

velocity vector with components (u, υ); normalized byV

v i :

nodal velocities in a finite element

v s :

velocity of the solid surface; zero in this study

Ws :

Weissenberg number;λV/h

W :

width of the die normal to thexy-plane

X :

position vector with components (X, Y)

β :

slip coefficient; normalized byh/η

\(\dot \gamma \) :

rate of deformation tensor; normalized byV/h

\(\dot \varepsilon \) :

elongation rate; dimensionless

λ :

relaxation time of main fluid

η :

shear viscosity of main fluid

η ex :

extensional viscosity (τxx — τyy)\(\dot \varepsilon \)

ϕ :

finite element shape function for velocity

ψ :

finite element shape function for pressure and stress

τ :

extra stress; normalized byηV/h

τ i :

nodal value of extra stress in an element

∂ :

partial differentiation

∇ :

gradient operator

References

  1. Dealy JM (1978) J Non-Newtonian Fluid Mech 4:9

    Google Scholar 

  2. Winter HH, Macosko CW, Bennett KE (1979) Rheol Acta 18:323

    Google Scholar 

  3. Macosko C, Ocansey MA, Winter HH (1982) J Non-Newtonian Fluid Mech 11:301

    Google Scholar 

  4. Park HS (1984) Planar Extension of Polystyrene Melts in Stagnation Flow Dies. MS Thesis, Univ. of Massachusetts

  5. Malone MF (1979) Numerical Simulation of Hydrodynamics Problems in Polymer Processing. PhD Thesis, Univ. of Massachusetts

  6. Baker AJ (1983) Finite Element Computational Fluid Mechanics. Hemisphere Publishing Corporation, Washington D.C.

    Google Scholar 

  7. LeBlanc JV (1985) Analysis of an Upper-Convected Maxwell Model in Viscoelastic Polymer Flow Simulation. PhD Thesis, Univ. of Massachusetts

  8. Navier M (1827) Memoire Sur Les Du Mouvement Des Fluides. Academie des Sciences, Series 2, TV1: 389

  9. Silliman WJ, Seriven LE (1980) J Comput Phys 34:287

    Google Scholar 

  10. Strang G, Fix GE (1974) An Analysis of the Finite Element Method. Prentice-Hall, Englewood Cliffs, NJ

    Google Scholar 

  11. Berker A, Lilleleht LU (1977) Ind Eng Chem Fund 16:425

    Google Scholar 

  12. Crochet MJ, Davies AR, Walters K (1984) Numerical Simulation of Non-Newtonian Flows. Elsevier, New York

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Union Camp Corporation, P.O. Box 412, 08542-0412, Princeton, NJ, USA

    J. V. Le Blanc

  2. Department of Chemical Engineering, Goessmann Laboratory, University of Massachusetts, 01003-0011, Amherst, Mass., USA

    M. F. Malone

Authors
  1. J. V. Le Blanc
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. F. Malone
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Le Blanc, J.V., Malone, M.F. Simulation of viscoelastic stagnation flow. Rheol Acta 25, 15–22 (1986). https://doi.org/10.1007/BF01369975

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF01369975

Key words

Search

Navigation