Skip to main content
SpringerLink
Log in

Control of Discrete Fuzzy Systems: Uncertainty and Guaranteed Performance

  • Published:
Dynamics and Control

Abstract

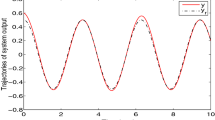
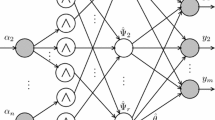
Robust control designs for a discrete Takagi and Sugeno (T-S) fuzzy model are proposed. The T-S fuzzy model contains (possibly fast) time-varying uncertainty. First, a switching-type robust control is shown to stabilize the T-S fuzzy model asymptotically. Second, a saturation-type robust control is shown to render the T-S model practically stable. In both designs, only the bound of uncertainty is needed. The effectiveness of proposed designs is analyzed rigorously and illustrated by simulations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Chen, C. L., Chen, P. C., and Chen, C. K., “Analysis and design of fuzzy control system,” Fuzzy Sets and Systems, vol. 57, pp. 125-140, 1993.

    Google Scholar 

  2. Corless, M. J. and Leitmann, G., “Continuous state feedback guaranteeing uniform ultimate boundedness for uncertain dynamic systems,” IEEE Transactions on Automatic Control, vol. AC-26, pp. 1139-1144, 1981.

    Google Scholar 

  3. Corless, M. and Manela, J., “Control of uncertain discrete-time systems,” Proceedings of the American Control Conference, pp. 515-520, Seatle, WA, 1986.

  4. Hirota, K., Arai, A., and Hachisu, S., “Fuzzy controlled robot arm playing two-dimensional ping-pong game,” Fuzzy Sets and Systems, vol. 32, pp. 140-1159, 1989.

    Google Scholar 

  5. Lee, T. S., Chen, Y. H., and Chuang, C.-H., “Uncertainty-bound based control design for matched and mismatched fuzzy systems,” submitted.

  6. Magana, M. E. and Zak, S. H. “Robust state feedback stabilization of discrete-time uncertain dynamical systems,” IEEE Transactions on Automatic Control, vol. AC-33, pp. 887-891, 1988.

    Google Scholar 

  7. Noble, B. and Daniel, J. W., Applied Linear Algebra, 3rd ed., Prentice Hall: Englewood Cliffs, NJ, 1988.

    Google Scholar 

  8. Sugeno, M. and Nishida, M., “Fuzzy control of model car,” Fuzzy Sets and Systems, vol. 16, pp. 103-113, 1985.

    Google Scholar 

  9. Takagi, T. and Sugeno, M., “Fuzzy identification of systems and its applications to modeling and control,” IEEE Transactions on Systems, Man, and Cybernetics, vol. 15, pp. 116-132, 1985.

    Google Scholar 

  10. Tanaka, K. and Sugeno, M., “Stability analysis and design of fuzzy control systems,” Fuzzy Sets and Systems, vol. 45, pp. 135-156, 1992.

    Google Scholar 

  11. Tanaka, K., “Stability and stabilzability of fuzzy-neural-linear control systems,” IEEE Transactions on Fuzzy Systems, vol. 3, pp. 438-447, 1995.

    Google Scholar 

  12. Yasunobu, S. and Miyamoto, S., “Automatic train operation by predictive fuzzy control,” in Industrial Application of Fuzzy control, M. Sugeno (ed.), North-Holland: Amsterdam, pp. 1-18, 1985.

    Google Scholar 

  13. Zhao, J., Wertz, V., and Gorez, R., “Linear TS fuzzy model based robust stabilizing controller design,” in Proceedings of the 34th Conference on Decision & Control, New Orleans, LA, pp. 255-260, 1995.

Download references

Author information

Authors and Affiliations

  1. School of Aerospace Engineering, Georgia Institute of Technology, Atlanta, Georgia

    T. S. Lee

  2. The George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, Georgia

    Y. H. Chen

  3. School of Aerospace Engineering, Georgia Institute of Technology, Atlanta, Georgia

    C.-H. Chuang

Authors
  1. T. S. Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Y. H. Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. C.-H. Chuang
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Lee, T.S., Chen, Y.H. & Chuang, CH. Control of Discrete Fuzzy Systems: Uncertainty and Guaranteed Performance. Dynamics and Control 8, 83–106 (1998). https://doi.org/10.1023/A:1008231013911

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1008231013911

Search

Navigation