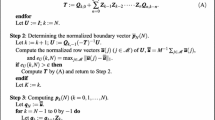Abstract
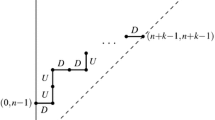
We apply the lattice path counting method to the analysis of the transientM/M/c queueing system. A closed-form solution is obtained for the probability of exactlyi arrivals andj departures within a time interval of lengtht in anM/M/c queueing system that is empty at the initial time. The derivation of the probability is based on the counting of paths from the origin to(i,j) on thexy-plane, that have exactly rd x-steps whose depth from the liney=x isd (d=0,1,...,c−1). The closed-form solution has an expression useful for numerical calculation.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
O.J. Boxma, The joint arrival and departure process for theM/M/1 queue, Stat. Neerlandica 38 (1984) 199–208.
W. Böhm and S.G. Mohanty, The transient solution ofM/M/1 queues under(M, N)-policy. A combinatorial approach, J. Stat. Plann. Inference 34 (1993) 23–33.
D.G. Champernowne, An elementary method of the solution of the queueing problem with a single server and constant parameter, J. Roy. Stat. Soc. Ser. B18 (1956) 125–128.
D. Gross and C.M. Harris,Fundamentals of Queueing Theory (Wiley, New York, 1985).
J. Medhi,Stochastic Models in Queueing Theory (Academic Press, New York, 1991).
S.G. Mohanty,Lattice Path Counting and Applications (Academic Press, New York, 1979).
S.G. Mohanty and W. Panny, A discrete-time analogue of theM/M/1 queue and the transient solution: A geometric approach, Sankhyā, Ser. A, 52 (1990) 364–370.
P.R. Parthasarathy, A transient solution to anM/M/1 queue: a simple approach, Adv. Appl. Prob. (1987) 997–998.
P.R. Parthasarathy and M. Sharafali, Transient solution to the many server Poisson queue: a simple approach, J. Appl. Prob. 26 (1989) 584–594.
C.D. Pegden and M. Rosenshine, Some new results for theM/M/1 queue, Manag. Sci. 28 (1982) 821–828.
T.L. Saaty, Time dependent solution of many server Poisson queue, Oper. Res. 8 (1960) 755–772.
K. Sen and J.L. Jain, Combinatorial approach to Markovian queueing models, J. Stat. Plann. Inference 34 (1993) 269–279.
K. Sen, J.L. Jain and J.M. Gupta, Lattice path approach to transient solution ofM/M/1 with (0,k) control policy, J. Stat. Plann. Inference 34 (1993) 259–267.
O.P. Sharma,Markovian Queues (Ellis Horwood, Chichester, 1990).
L. Takács, A generalization of the ballot problem and its application in the theory of queues, J. Amer. Stat. Ass. 57 (1962) 327–337.
L. Takács, A single server queues with recurrent input and exponentially distributed service times, Oper. Res. 10 (1962) 395–399.
L. Takács, A combinatorial method in the theory of queues, SIAM J. Appl. Math. 10 (1962) 691–694.
D. Towsley, An application of the reflection principle to the transient analysis of theM/M/1 queue, Naval. Res. Logist. 34 (1987) 451–456.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Muto, K., Miyazaki, H., Seki, Y. et al. Lattice path counting andM/M/c queueing systems. Queueing Syst 19, 193–214 (1995). https://doi.org/10.1007/BF01148946
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF01148946