The Padé interpolation method applied to additive difference Painlevé equations

Abstract

We study Padé interpolation problems on an additive grid, related to additive difference (d-) Painlevé equations of type $E_7^{(1)}$, $E_6^{(1)}$, $D_4^{(1)}$ and $A_3^{(1)}$. By choosing suitable Padé problems, we can derive time evolution equations, scalar Lax pairs of contiguous type and determinant formulae of special solutions given in terms of hypergeometric functions, for the corresponding d-Painlevé equations.

Appendix A. Sufficiency for the compatibility of the Lax pair

In Sect. 3.1, we gave the d-$E_7^{(1)}$ equation (3.7) as the necessary condition for the compatibility of the Lax pair (3.10). In this appendix, we prove that the d-$E_7^{(1)}$ equation is the sufficient condition for the compatibility of the Lax pair.

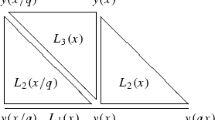
As in Fig. 3, eliminating $\overline{y}(x)$ and $\overline{y}(x-1)$ from $L_2(x)= L_2(x-1)=L_3(x)=0$ (3.6), one constructs the linear equation $L_1=0$ among $y(x+1)$, y(x) and $y(x-1)$, where

$$\begin{aligned} \displaystyle L_1(x)= & {} \frac{(x-a_0-b_0)\prod _{i=1}^3(x+a_i)}{x-f}y(x+1)+\frac{x\prod _{i=1}^3(x+b_i-1)}{(x-f-1)}y(x-1)\nonumber \\&\displaystyle -\frac{1}{x-h}\Big [\frac{A_2(x)(x-g)}{x-f}+\frac{V(x-1)}{(x-f-1)(x-g-1)}\Big ]y(x) \end{aligned}$$

(A.1)

and

$$\begin{aligned} V(x)=(x-h)(x-h+1)A_1(x)-C_0C_1(x-f)(x-\overline{f}). \end{aligned}$$

(A.2)

Here, the variable $\overline{f}$ and the product $C_0C_1$ in (A.2) should be viewed as functions in terms of f and g, and they are determined in (3.7) and (3.8), respectively. Expression $L_1$ (A.1) is rewritten into (3.10) by using (3.7) and (3.8).

Lemma A.1

The expression $(x-f)(x-f-1)L_1(x)$ (A.1) (or (3.10)) has the following characterization:

(i) It is a linear equation among $y(x+1)$, y(x) and $y(x-1)$, and the coefficients of these terms are polynomials of degree 5 in x.

(ii) The coefficients of $y(x+1)$ (resp. $y(x-1)$) have zeros at $x=-a_1$,$-a_2$,$-a_3$, $a_0+b_0$ (resp. $x=-b_1+1$,$-b_2+1$, $-b_3+1$, 0).

(iii) Under the conditions

$$\begin{aligned}&\displaystyle \frac{y(x+1)}{y(x)}=1+\frac{a_0}{x}+\frac{a_0(a_0-1)/2}{x^2}+\frac{w}{x^3} +O\Big (\frac{1}{x^4}\Big ),\nonumber \\&\quad \displaystyle \frac{y(x-1)}{y(x)}=1-\frac{a_0}{x}+\frac{a_0(a_0-1)/2}{x^2}-\frac{w}{x^3}+O\Big (\frac{1}{x^4}\Big ), \end{aligned}$$

(A.3)

the terms $x^5, \ldots , x^2$ in the expression $(x-f)(x-f-1)L_1(x)$ vanish, namely $(x-f)(x-f-1)L_1(x)=O(x^1)$ around $x=\infty$. Here, $w \in {\mathbb {C}}$ is an arbitrary constant.

(iv) The equation $(x-f)(x-f-1)L_1=0$ holds at the two points $x=f, f+1$, where

$$\begin{aligned} {\displaystyle \frac{y(f+1)}{y(f)}} ={\displaystyle \frac{(f+b_1)(f+b_3)(f-g)}{(f+a_2)(f-a_0-b_0)(f-h)}}. \end{aligned}$$

(A.4)

Conversely, the expression $(x-f)(x-f-1)L_1(x)$ is uniquely characterized by these properties $(i)-(iv)$. $\square$

Proof

The property (i) is obtained by relations (3.8). Concretely, the expression $\frac{V(x-1)}{x-g-1}$ reduces to a polynomial of degree 5 in x under the first relation of (3.8). Moreover, the coefficient of the term y(x) is obtained as a polynomial of degree 5 in x by using the second relation of (3.8). The property (ii) is trivial. The property (iii) can easily be checked by condition (A.3). The property (iv) follows by substituting $x=f, f+1$ into the equation $L_1(x)=0$. $\square$

Remark A.2

Two points $x=f, f+1$ are apparent singularities in the sense that at those two points the equation $(x-f)(x-f-1)L_1(x)=0$ (A.1) is satisfied under the same condition (in this case (A.4)). $\square$

Similarly, as in Fig. 4, eliminating y(x) and $y(x+1)$ from $L_2(x)= L_3(x)=L_3(x+1)=0$ (3.6), we obtain the linear equation $L_1^*=0$ among $\overline{y}(x+1)$, $\overline{y}(x)$ and $\overline{y}(x-1)$, where

$$\begin{aligned} \displaystyle L_1^*(x)= & {} \frac{(x-a_0-b_0)(x+a_1+1)(x+a_2)(x+a_3+1)}{x-\overline{f}}\overline{y}(x+1)\nonumber \\&\displaystyle +\frac{x(x+b_1)(x+b_2-1)(x+b_3)}{(x-\overline{f}-1)}\overline{y}(x-1)\nonumber \\&\displaystyle -\frac{1}{x-h}\Big [\frac{A_2(x)(x-g-1)}{x-\overline{f}-1}+\frac{V(x)}{(x-\overline{f})(x-g)}\Big ]y(x). \end{aligned}$$

(A.5)

Fig. 4

Derivation of $L_1^*(x)$

The following Lemma (and its proof) is similar to Lemma A.1.

Lemma A.3

The expression $(x-\overline{f})(x-\overline{f}-1)L_1^*(x)$ (A.5) has the following characterization:

(i) It is a linear three term expression among $\overline{y}(x+1)$ and $\overline{y}(x)$ and $\overline{y}(x-1)$, and the coefficients of these terms are polynomials of degree 5 in x.

(ii) The coefficients of $\overline{y}(x+1)$ (resp. $\overline{y}(x-1)$) have zeros at $x=-a_1-1$,$-a_2$,$-a_3-1$, $a_0+b_0$ (resp. $x=-b_1$,$-b_2+1$, $-b_3$, 0).

(iii) Under the conditions

$$\begin{aligned}&\displaystyle \frac{\overline{y}(x+1)}{\overline{y}(x)}=1+\frac{a_0}{x} +\frac{\overline{a}_0(a_0-1)/2}{x^2}+\frac{\overline{w}}{x^3}+O\Big (\frac{1}{x^4}\Big ),\nonumber \\&\quad \displaystyle \frac{\overline{y}(x-1)}{\overline{y}(x)}=1-\frac{a_0}{x} +\frac{a_0(a_0-1)/2}{x^2}-\frac{\overline{w}}{x^3}+O\Big (\frac{1}{x^4}\Big ), \end{aligned}$$

(A.6)

the terms $x^5, \ldots , x^2$ in the expression $(x-\overline{f})(x-\overline{f}-1)L_1^*(x)$ vanish, namely $(x-\overline{f})(x-\overline{f}-1)L_1^*(x)=O(x^1)$ around $x=\infty$. Here, $w \in {\mathbb {C}}$ is the same arbitrary constant as in (A.3).

(iv) The equation $(x-\overline{f})(x-\overline{f}-1)L_1^*=0$ holds at the two points $x=\overline{f}, \overline{f}+1$ where

$$\begin{aligned} {\displaystyle \frac{\overline{y}(\overline{f}+1)}{\overline{y}(\overline{f})}} ={\displaystyle \frac{(\overline{f}+b_2)(\overline{f}+1)(\overline{f}+h-1)}{(\overline{f}+a_1+1)(\overline{f}+a_3+1)(\overline{f}-g)}}. \end{aligned}$$

(A.7)

Conversely, the expression $(x-\overline{f})(x-\overline{f}-1)L_1^*(x)$ is uniquely characterized by these properties $(i)-(iv)$. $\square$

The sufficiency for the compatibility means that $T(L_1(x))\propto L_1^*(x)$ holds when the d-$E_7^{(1)}$ equation (3.7) is satisfied. In order to prove the sufficiency, we characterize $L_1$ and $L_1^*$ as polynomials in terms of x, and compare these characterizations.

Proposition A.4

The linear equations $L_1=0$ and $L_2=0$ (3.10) for the unknown function y(x) are compatible if and only if the d-$E_7^{(1)}$ equation (3.7) is satisfied. $\square$

Proof

The compatibility means that the shift operator T changes the equation $L_1=0$ into the equation $L_1^{*}=0$, i.e., the commutativity in Fig. 5.

Fig. 5

Compatibility of $L_1(x)$ and $L_1^*(x)$

This commutativity is almost clear from the characterizations (i), (ii) of the equation $L_1=0$ (respectively $L_1^*=0$) in Lemma A.1 (respectively Lemma A.3). The remaining task is to check that the operator T changes expression (A.4) into expression (A.7), utilizing the characterization (iii) of the equation $L_1=0$ (respectively $L_1^*=0$) and the first part of equation (3.7). $\square$

As the point of the proof, the following two are applied to type d-$E_7^{(1)}$ together: The first is that the equation $L_1(f,\overline{f}, g)=0$ in terms of f, $\overline{f}$ and g is derived from the equations $L_2(f,g)=0$ and $L_3(\overline{f},g)=0$ (see [17, 33, 48, 49]). The second is that the equation $L_1(f,\overline{f}, g)=0$ is characterized as a polynomial in terms of x (see [25, 28]).