Measurement of crystallographic orientation of quartz crystal using Raman spectroscopy: application to entrapped inclusions

Abstract

Raman spectroscopy has been widely used in mineralogy and petrology for identifying mineral phases. Some recent applications of Raman spectroscopy involve measuring the residual pressure of mineral inclusions, such as quartz inclusions in garnet host, to recover the entrapment pressure condition during metamorphism. The crystallographic orientations of entrapped inclusions and host are important to know for the modelling of their elastic interaction. However, the analysis of tiny entrapped mineral inclusions using EBSD technique requires time consuming polishing. The crystallographic orientations can be measured using polarized Raman spectroscopy, as the intensities of Raman bands depend on the mutual orientation between the polarization direction of the laser and the crystallographic orientation of the crystal. In this study, the Raman polarizability tensor of quartz is first obtained and is used to fit arbitrary orientations of quartz grains. We have implemented two rotation methods: (1) sample rotation method, where the sample is rotated on a rotation stage, and (2) polarizer rotation method, where the polarization directions of the incident laser and the scattered Raman signal are parallel and can be rotated using a circular polarizer. The precision of the measured crystallographic orientation is systematically studied and is shown to be ca. 0.25 degrees using quartz wafers and quartz plates that are cut along known orientations. It is shown that the orientation of tiny mineral inclusions (ca. 2–5 μm) can be precisely determined and yield consistent results with EBSD.

Introduction

Unraveling the mechanisms underlying mineralogical-petrological and geodynamical processes often requires a knowledge of the crystallographic orientation of the minerals found in the studied sample material. Crystallographic orientation has been mostly measured with the electron backscattered diffraction (EBSD) technique. One critical limitation is that EBSD only allows measurement at a polished sample surface and the measured grains must be exposed. However, in many cases, it is necessary to measure the orientations of entrapped inclusions, or at subsurface mineral grains if the sample is coated with a thin-film that hinders the application of EBSD technique. One relevant case for which knowledge of the crystallographic orientation is of interest is Raman elastic thermobarometry, where the residual stress (strain) is measured using Raman spectroscopy for the inclusions sealed in host grains to recover the pressure or temperature conditions when entrapment occurred at depth (e.g., Enami et al. 2007). The generation of the residual stress is due to the different elasticity and thermal expansion between the inclusion and host (Rosenfeld and Chase 1961; Zhang 1998). The quartz-in-garnet elastic barometry technique is a good example of this. Recently this technique has become more and more popular and has been widely applied in many petrological studies on metamorphic rocks (e.g., Korsakov et al. 2009; Ashley et al. 2014; Kohn 2014; Kouketsu et al. 2014; Zhong et al. 2021b; Taguchi et al. 2019; Zhong et al. 2019; Alvaro et al. 2020; Dunkel et al. 2020; Schwarzenbach et al. 2021; Szczepański et al. 2021). The main advantage of the Raman elastic thermobarometry is that it is not relying on interpretations of the complex history of phase relations during the bulk chemical equilibrium evolution, and it does not require the presences of high-P minerals such as coesite, phengite, omphacite, lawsonite, as they are prone to retrograde mineral chemical modification or even breakdown reactions. Moreover, large, consistent, and comprehensive data sets of pressure estimates can be generated as entrapment pressures can be obtained on a regional scale from various lithologies so that a coherent geodynamic evolution history can be reconstructed (e.g.,Bayet et al. 2018; Groß et al. 2020). The technique is appealing due to its independence from phase equilibria and chemical thermobarometry techniques, but has the limitation that the orientation of mineral inclusion cannot be easily obtained to model the elastic interaction between the inclusion and host. The current model considers isotropic elasticity of both the inclusion and host, thus the crystallographic orientation is irrelevant (e.g.,Zhang 1998; Guiraud and Powell 2006). However, the elastic properties of minerals are not actually isotropic and when elastic anisotropy is considered, the mutual orientation between the crystallographic axes and the inclusion shape (e.g., the long and short axis for near-ellipsoid shape) will have an effect on the final residual stress and strain state preserved by the inclusion (Zhong et al. 2021a).

In practice, it is time-consuming and destructive to use EBSD to measure the entrapped inclusion because it requires first measuring the inclusion with Raman spectroscopy and subsequently polishing the thin-section to an appropriate depth to expose the measured inclusion (Campomenosi et al. 2018). Fortunately, it is possible to directly measure the crystallographic orientation of tiny entrapped mineral inclusions in situ using Raman spectroscopy. The main advantage is that (1) the inclusion does not need to be exposed so that the residual stress is preserved; (2) the acquisition is convenient and post-processing is relatively simple compared to, e.g., EBSD; (3) Raman wavenumber shift compared to a stress-free standard can be simultaneously obtained.

One difficulty related to the measurement of crystallographic orientations of anisotropic minerals using Raman spectroscopy is the birefringence effect. When a linearly polarized laser beam reaches the surface of an anisotropic crystal, the laser splits into two beam paths with different polarization directions. They will both generate Raman scattering effects and interfere with each other. This effect has been hindering the determination of Raman polarizability tensors and the use of Raman spectroscopy to measure the crystallographic orientation (Porto et al. 1966). A conventional method dealing with this obstacle is to introduce a phenomenological parameter called “phase difference” to fit the experimental data (e.g.,Kim et al. 2015; Livneh et al. 2006; Sander et al. 2012; Strach et al. 1998). To resolve the birefringence effect, Kranert et al. (2016a; b) applied the Jones matrix to treat the phase difference and it is theoretically shown that the apparent phase difference generated by the birefringence effect should approach a fixed value (π/2) if the Raman scattering is averaged over a sufficient depth. The same apparent phase difference of π/2 has been experimentally confirmed in Zheng et al. (2018) on wurtzite crystals. In this work, we focus on quartz crystals and obtain the Raman polarizability tensor of quartz and developed a framework to fit the crystallographic orientation of an arbitrarily oriented quartz crystal. We also provide experimental confirmation on the apparent phase difference that supports the work by Kranert et al. (2016a; b). In addition, we systematically investigate the precision of the crystallographic orientation measured using Raman spectroscopy. The orientation of quartz inclusions from natural samples is also measured and the data of exposed inclusions are cross-validated with EBSD.

Background theory

Quartz is a complex piezoelectric crystal with D₃ symmetry. It is shown by the group theory that quartz has 27 normal vibration modes, among the Raman active modes 4 are totally symmetric (A₁) and 4 are doubly degenerate (E) modes (She et al. 1971). In this study, we focus on the four totally symmetric A₁ Raman bands that are located at the wavenumber around 464, 206, 360 and 1080 cm⁻¹, and four doubly degenerate E bands that are located at around 128, 700, 265 and 1160 cm⁻¹. The doubly degenerate E mode Raman bands contain contributions consisting of the longitudinal optical (LO) and transverse optical (TO) components but are not resolved due to their proximity in wavenumber. In this work, the summed intensity of LO and TO components is used for crystallographic orientation measurement. The Raman band intensity is predicted using the following classical formula (e.g., Loudon 1964):

$$I_{s} \propto \left| {{\varvec{e}}_{{\varvec{i}}}^{{\mathbf{T}}} \cdot {\varvec{\alpha}} \cdot {\varvec{e}}_{{\varvec{s}}} } \right|^{2} ,$$

(1)

where ${\varvec{e}}_{{\varvec{i}}}$ and ${\varvec{e}}_{{\varvec{s}}}$ are the electric field vectors of the incident and scattered light, respectively, and α is the 2nd-rank polarizability tensor of the crystal normal phonon mode, which is generally represented by a symmetrical 3-by-3 matrix. In a backscattering geometry, which is typical of Raman experiments with a microscope, both ${\varvec{e}}_{{\varvec{i}}}$ and ${\varvec{e}}_{{\varvec{s}}}$ are perpendicular to the direction of the laser, which is along the z-axis of the laboratory coordinate system (Fig. 1). In this case, one can restrict the considerations to the x–y plane and consequently, ${\varvec{e}}_{{\varvec{i}}}$ and ${\varvec{e}}_{{\varvec{s}}}$ become two-dimensional (2D) vectors with x and y components only, while α will be represented by a 2-by-2 matrix without the z-component of the original 3-by-3 polarizability tensor.

Fig. 1

a Photograph of the microscopy setup. Rotation stage and notched rotation rings with a circular polarizer attached to the upper ring are included that allow the sample and polarizer rotation, respectively. The Cartesian coordinates are shown in the upper left corner. b Schematic diagram of sample rotation setup. The sample can be rotated using the rotation stage. The incident laser and scattered Raman signal both cross a fixed linear polarizer in the plastic plate. c Schematic diagram of polarizer rotation setup. The sample is fixed on a x–y moving stage. The circular polarizer can be rotated using a pair of 3D printed notched rotation rings placed above the objective as shown in a. The circular polarizer allows the polarization direction of the laser and the scattered Raman signal to be rotated in 10 degrees increments. The upper and lower rings are identical and have 36 notches that match each other

For anisotropic crystal, the Jones matrix is added into Eq. 1, which accounts for the phase difference of the incident and scattered light (Kranert et al. 2016a; Mao et al. 2017).

$$I_{s} \propto \left| {{\varvec{e}}_{{\varvec{i}}}^{{\mathbf{T}}} \cdot {\varvec{J}} \cdot {\varvec{\alpha}} \cdot {\varvec{J}} \cdot {\varvec{e}}_{{\varvec{s}}} } \right|^{2} ,$$

(2)

where ${\varvec{J}}$ is the 2D Jones matrix (on x–y plane), which can be expressed as below (Jones 1941):

$${\varvec{J}} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & {e^{i\chi } } \\ \end{array} } \right]\,.$$

(3)

For a crystal placed at an arbitrary orientation, the rotation matrices are introduced as below following the Z–X–Z Euler rotation order (the Bunge convention) using the active rotation as sketched in Fig. 2:

$$\begin{gathered} {\varvec{R}}_{{{\varvec{Z}}1}} = \left[ {\begin{array}{*{20}c} {{\text{cos}}\left( {\phi_{1} } \right)} & { - {\text{sin}}\left( {\phi_{1} } \right)} & 0 \\ {{\text{sin}}\left( {\phi_{1} } \right)} & {{\text{cos}}\left( {\phi_{1} } \right)} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right] \hfill \\ {\varvec{R}}_{{\varvec{X}}} \, = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {{\text{cos}}\left( \Phi \right)} & { - {\text{sin}}\left( \Phi \right)} \\ 0 & {sin\left( \Phi \right)} & {{\text{cos}}\left( \Phi \right)} \\ \end{array} } \right] \hfill \\ {\varvec{R}}_{{{\varvec{Z}}2}} = \left[ {\begin{array}{*{20}c} {{\text{cos}}\left( {\phi_{2} } \right)} & { - {\text{sin}}\left( {\phi_{2} } \right)} & 0 \\ {{\text{sin}}\left( {\phi_{2} } \right)} & {{\text{cos}}\left( {\phi_{2} } \right)} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right] \hfill \\ \end{gathered}$$

(4)

Fig. 2

Schematic diagram showing the active rotation method used in this work. The rotation follows the Z–X–Z sequence (Bunge convention) and the crystal is rotated from a reference state as shown in a to the final state in d that coincides with the orientation in the sample

Therefore, the rotated Raman polarizability tensor α is expressed as:

$${\varvec{\alpha}} = \left[ {\begin{array}{*{20}c} {\alpha_{11}^{{3{\text{D}}}} } & {\alpha_{12}^{{3{\text{D}}}} } \\ {\alpha_{21}^{{3{\text{D}}}} } & {\alpha_{22}^{{3{\text{D}}}} } \\ \end{array} } \right],\,\,{\text{where}}\,\,{\varvec{\alpha}}^{{3{\mathbf{D}}}} = {\varvec{R}}_{{{\varvec{Z}}1}} {\varvec{R}}_{{\varvec{X}}} {\varvec{R}}_{{{\varvec{Z}}2}} {\varvec{\alpha}}_{{\varvec{U}}} {\varvec{R}}_{{{\varvec{Z}}2}}^{{\varvec{T}}} {\varvec{R}}_{{\varvec{X}}}^{{\varvec{T}}} {\varvec{R}}_{{{\varvec{Z}}1}}^{{\varvec{T}}}$$

(5)

where ${\varvec{\alpha}}_{{\varvec{U}}}$ is the unrotated 3-by-3 Raman polarizability tensor and ${\varvec{\alpha}}^{{3{\mathbf{D}}}}$ is the rotated 3-by-3 polarizability tensor from the sample reference frame to the crystal reference frame. The rotated ${\varvec{\alpha}}$ tensor only takes the first 2-by-2 components of ${\varvec{\alpha}}^{{3{\mathbf{D}}}}$ because the crystal interacts with the laser with its electric field vector on the x–y plane. It is noted that in this study, the active rotation method has been applied here (see the difference between active and passive rotation in Morrison and Parker 1987).

As the crystal is rotated, its fast and slow axes projected on the x–y plane will only depend on the first Euler angle $\phi_{1}$ due to quartz’s symmetry. Therefore, the Jones matrix is also rotated by an angle $\phi_{1}$ to align its fast and slow axes in accordance with the projected crystallographic c and a-axes on the x–y plane.

$${\varvec{J}} = \left[ {\begin{array}{*{20}c} {{\text{cos}}\left( {\phi_{1} } \right)} & { - {\text{sin}}\left( {\phi_{1} } \right)} \\ {{\text{sin}}\left( {\phi_{1} } \right)} & {{\text{cos}}\left( {\phi_{1} } \right)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & {e^{i\chi } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\text{cos}}\left( {\phi_{1} } \right)} & {{\text{sin}}\left( {\phi_{1} } \right)} \\ { - {\text{sin}}\left( {\phi_{1} } \right)} & {{\text{cos}}\left( {\phi_{1} } \right)} \\ \end{array} } \right]\,.$$

(6)

For the totally symmetric vibration mode A₁ of a crystal with D₃ symmetry, the fundamental (unrotated) Raman polarizability tensor in Eq. 5 is expressed as follows (Loudon 1964):

$${\varvec{\alpha}}_{{\varvec{A}}} = \left[ {\begin{array}{*{20}c} a & 0 & 0 \\ 0 & a & 0 \\ 0 & 0 & b \\ \end{array} } \right]$$

(7)

where a and b are the Raman polarization components. This tensor is axially symmetric where its crystallographic c-axis is parallel to the Cartesian z-axis. The doubly degenerate E mode has two components, E(x), and E(y), where x and y refer to the phonon-mode polarity, whose fundamental polarizability tensors are given as follows (Loudon 1964):

$$\begin{gathered} {\varvec{\alpha}}_{{{\varvec{Ex}}}} = \left[ {\begin{array}{*{20}c} c & 0 & 0 \\ 0 & { - c} & d \\ 0 & d & 0 \\ \end{array} } \right] \hfill \\ {\varvec{\alpha}}_{{{\varvec{Ey}}}} = \left[ {\begin{array}{*{20}c} 0 & { - c} & { - d} \\ { - c} & 0 & 0 \\ { - d} & 0 & 0 \\ \end{array} } \right] \hfill \\ \end{gathered}$$

(8)

The incident (${\varvec{e}}_{{\varvec{i}}}$) and the scattered (${\varvec{e}}_{{\varvec{s}}}$) light have their electric field vector on the x–y plane, thus can be described by an angle $\theta$ that is measured between 0 and 2π counter clockwise from the x-axis on the x–y plane. Here, we restrict our work to the parallel polarization setup, thus ${\varvec{e}}_{{\varvec{i}}} = {\varvec{e}}_{{\varvec{s}}}$ holds. The electric field vectors ${\varvec{e}}_{{\varvec{i}}}$ and ${\varvec{e}}_{{\varvec{s}}}$ are expressed as follows (z-component is omitted):

$${\varvec{e}}_{{\varvec{i}}} = {\varvec{e}}_{{\varvec{s}}} = \left[ {\begin{array}{*{20}c} {{\text{cos}}\left( \theta \right)} & {{\text{sin}}\left( \theta \right)} \\ \end{array} } \right]$$

(9)

The intensity of A₁ mode Raman band is obtained by substituting $\alpha_{A}$ from Eq. 7 into Eq. 5 and then back into Eq. 2. The intensity of the E mode Raman band can be obtained by substituting both ${\varvec{\alpha}}_{{{\varvec{Ex}}}}$ and ${\varvec{\alpha}}_{{{\varvec{Ey}}}}$ into Eq. 5 separately, and then substituting them into Eq. 2 and summing the two intensities to get the total intensity. A general form is derived for both A₁ and E modes as a function of $\theta$ as follows:

$$I_{s} \propto \left| {\left[ {C_{1} {\text{cos}}\left( \theta \right)^{2} + C_{2} {\text{sin}}\left( \theta \right)^{2} + C_{3} {\text{sin}}\left( {2\theta } \right)} \right]^{2} } \right|$$

(10)

Note that the square is applied inside the absolute symbol and the result will be different if it is outside. This is the general form that applies to both A₁ and E mode depending on the complex coefficients $C_{1}$, $C_{2}$ and $C_{3}$, which are controlled by the Euler angle of the crystal, the birefringence parameter $\chi$, and the Raman polarizability tensor. The explicit expression of the complex coefficients $C_{1}$, $C_{2}$ and $C_{3}$ for A₁ and E modes are given in the Appendix.

When the quartz crystal is placed at a specific orientation, e.g., the crystallographic c-axis aligned perpendicular to the direction of incident laser, we are able to substantially simplify the above expression. For a quartz plate cut along the plane formed by its c and a-axes, the predicted intensity of A and E mode can be explicitly expressed as below by substituting $\phi_{1} = \phi_{2} = 0$ and $\Phi = 90^{o}$ into $C_{1}$, $C_{2}$ and $C_{3}$ to get:

$$\begin{gathered} I_{A} \propto a^{2} cos\left( \theta \right)^{4} + b^{2} sin\left( \theta \right)^{4} + \frac{1}{2}absin^{2} \left( {2\theta } \right)cos\left( {2\chi } \right) \hfill \\ I_{E} \propto c^{2} cos\left( \theta \right)^{4} + d^{2} sin\left( {2\theta } \right)^{2} \hfill \\ \end{gathered}$$

(11)

It is observed that the intensity of E mode Raman bands is not sensitive to the variation of the birefringence parameter $\chi$, while the A mode is. By measuring the intensity as a function of the orientation $\theta$, it is possible to fit for the Raman polarizability tensor and the birefringence parameter $\chi$. It has been shown by Kranert et al. (2016a; b) and Zheng et al. (2018) that in case the Raman scattering depth is sufficiently large, the apparent phase shift is $\pi /2$. Because the Jones matrix is multiplied twice on the Raman polarizability tensor in Eq. 2, the parameter $\chi$ should approach its theoretical value of $\pi /4$.

Samples and methods

Sample descriptions

Three fused single crystal quartz wafers were purchased from MicroChemicals.GmbH, Germany. The quartz wafers are X-cut, ST-cut and AT-cut with the uncertainty of the cutting angle less than 0.5 degrees. For the X-cut, the c-axis and a-axis are on the wafer plane. The ST-cut quartz wafer has an Euler angle $\Phi$ ca. 47.3 degree, and for the AT-cut quartz wafer the Euler angle $\Phi$ is ca. 54.7 degree. The thickness of the wafers is ca. 200 $\mu$ m. The optical transparency of the quartz wafers is very high, and no surface scratch or visible impurity can be observed under microscopy.

In addition, single-crystal Brazilian quartz were cut in two orientations corresponding to: (1) a plane parallel to the plane of the a and b-axes, i.e., perpendicular to the c-axis; (2) a plane with its normal vector inclined 50 degree to the c-axis, i.e., the $\Phi$ angle is 50 degrees. These two cuts were polished using fine sandpaper. The cutting was performed manually along a line drawn at the measured angle, thus the uncertainty is larger compared to the quartz wafer. We estimate the uncertainty to be 2 degrees due to the cutting process.

Raman spectroscopy and rotation method

Raman spectra were obtained with a Horiba Dilor Labram confocal Raman spectrometer using the 632.8 nm (red) line of He–Ne Laser at the Freie Universität Berlin. The focal length is 300 mm, the grating is 1800 grooves/mm, and the slit width was 100 µm. The used objectives are Olympus 10×, 20×, 50× and 100× and the confocal hole was set as 400 µm. The duration for each measurement was set at 1 to 2 min with 3–5 times repetition to obtain good signal to noise ratio.

The Raman spectra were measured while systematically varying the angle $\theta$ between the polarization direction and the sample. We have implemented two rotation techniques as shown in Fig. 1: (1) Sample rotation, where the sample is rotated using a rotation stage (Thorlabs) with an angular Vernier caliper. A linear polarizer (LPVISE100-A from Thorlabs with extinction ratio > 10,000 for the 633 nm laser) was placed above the sample within the microscope. (2) Polarizer rotation, where the incident and scattered laser beams pass through a rotatable circular polarizer (CP42HE of Edmund Optics, diameter 1.25 mm left-handed circular polarizer with valid wavelength range from 400 to 700 nm). The circular polarizer is made of a quarter waveplate and a linear polarizer. The linearly polarized laser first passes through the quarter waveplate and turns into an elliptically polarized light (or still linear polarized if it coincides with one of the axes). Then the light passes through the linear polarizer to turn into a linearly polarized light at a desired orientation. Compared to directly using a linear polarizer, this method avoids complete extinction when the linear polarizer is perpendicular to the incident polarized laser. The circular polarizer is placed into a ring that contains notches every 10 degree with notches facing downward. Another identical ring is facing upward so that the notches match each other. The circular polarizer is rotatable with this setup (Fig. 1). The notches rings are 3D printed. After each measurement, the upper notched ring together with the circular polarizer is rotated by 10 degrees. For polarizer rotation method, a rotation stage is not needed and a x–y moving stage is implemented instead for searching inclusions.

Fitting Raman polarizability tensor and crystallographic orientation

To fit the components of the Raman polarizability tensor, the X-cut quartz wafer (c-axis on the wafer plane) was measured with the sample rotation method. The Raman band intensities were recorded every 5 degrees using the rotation stage. Gaussian fits were performed using a self-written MATLAB script to obtain the intensity of Raman bands. Each band is fitted separately by choosing a wavenumber window that only include desired band. A first-order linear function with two unknown variables is added into the fitting equation to account for the background slope and background level (zero-truncation). The variables including the peak intensity, peak position, sigma, background slope and its zero-wavenumber truncation are simultaneously fitted using the least-square method (“lsqcurvefit” function with trust-region-reflective method in MATLAB 2017b). If two nearby peaks are convoluted (e.g., garnet host is present), two Gaussian distribution functions are simultaneously fitted so that the two peaks can be deconvoluted. The same fitting procedure have been described in Zhong et al. (2019).

The Eq. 11 describing the Raman band intensities with respect to the orientation of polarizer is used to obtain the Raman polarizability tensor. Non-linear optimization is performed using the MATLAB (2017b) function “fmincon” to fit the components of the Raman polarizability tensor. The fitted components of the Raman polarizability tensor are given in Table 1. The b component for totally symmetric A₁ mode, and d component for the doubly degenerate E mode are used to scale the a and c components, respectively. The uncertainties of the a/b and c/d ratios are determined using the bootstrap method (Efron and Tibshirani 1993). With the bootstrap method, the sets of orientations and intensities are randomly sampled with repetition and the coefficients of the Raman polarizability tensor are fitted using Eq. 11 for each randomly selected dataset. The standard deviations of the components for all Raman bands are calculated after 1000 iterations. The same approach in fitting phenomenological parameters can be found in details in Zhong et al. (2018).

Table 1 Fitted Raman polarizability tensor using the quartz wafer cut parallel to the c and a-axis plane

The sign of the components of the Raman polarizability tensor, i.e., a/b and c/d for A₁ and E modes, respectively, cannot be determined using Eq. 11. Therefore, the ST-cut quartz wafer is also used to aid the determination of the sign by trial and error. The a/b and c/d components with both positive and negative signs are tested on the intensities measured on the ST-cut quartz wafer and only one of them fit the measured data (the other being completely off), and the corresponding sign is selected as given in Table 1.

To fit the crystallographic orientation, we also used the MATLAB function “fmincon” to perform the non-linear minimization of the residual. The Raman intensity for an arbitrarily oriented quartz crystal can be described by Eq. 10, where the $C_{1}$, $C_{2}$ and $C_{3}$ variables are given in Appendix, which are functions of $\phi_{1}$, $\Phi$, $\phi_{2}$ and $\chi$. The 464 cm⁻¹ band intensity is used to scale the other band intensities. The 265 cm⁻¹ doubly degenerate band is not used in fitting the crystallographic orientation due to its low intensity and its strong neighboring 206 cm⁻¹ band. The total residual is formulated as follows:

$$Res = \sqrt {\sum\nolimits_{i}^{N} {\sum\nolimits_{j}^{M} {w_{i}^{2} \left( {\frac{{I_{i}^{fitted} \left( {\theta_{j} } \right)}}{{I_{464}^{fitted} \left( {\theta_{j} } \right)}} - \frac{{I_{i}^{data} \left( {\theta_{j} } \right)}}{{I_{464}^{data} \left( {\theta_{j} } \right)}}} \right)^{2} } } }$$

(12)

where $i$ denotes the index of Raman band with N being the total number of Raman bands that are used, $j$ denotes the index of the applied polarization angle $\theta$ during polarizer rotation or sample rotation with the total number of rotation $M$, $I_{i}^{fitted} \left( {\theta_{j} } \right)$ are the fitted ith Raman band intensity measured at the polarization angle $\theta_{j}$, $I_{464}^{fitted} \left( {\theta_{j} } \right)$ is the fitted 464 cm⁻¹ Raman band intensity at polarization angle $\theta_{j}$, and similarly $I_{i}^{data}$ are the measured intensity of the $i$ th Raman band. Weighting factors $w_{i}$ are applied to the involved Raman bands. In this study, we chose $w_{i} = 1/max\left[ {I_{i}^{data} \left( {\theta_{j} } \right)} \right]$ to normalize the Raman band intensities to unity, so that equal weight can be applied for fitting the crystallographic orientation.

The equation is programmed into MATLAB and the total residual is minimized by fitting the $\phi_{1}$, $\Phi$, $\phi_{2}$ and $\chi$ simultaneously. This equation is non-linear and a wrong initial guess may lead to convergence to a local minimum point. Therefore, we cycle through a set of initial guesses in the $\phi_{1}$, $\Phi$, $\phi_{2}$ space and obtain the best fit result based on the whole set that yields the lowest residual. The best-fitted Euler angles and $\chi$ correspond to the set of results that yield the lowest residual. The interval of the initial guesses for $\phi_{1}$, $\Phi$, $\phi_{2}$ is chosen to be 15 degrees, which is sufficient to guarantee the convergence to the global minima in this study.

Scanning electron microscopy and EBSD measurements

In this work, imaging and EBSD experiments were carried out using a Quanta 3D field emission scanning electron microscope (Thermo Fisher Scientific, former FEI) equipped with an EDAX energy dispersive spectrometer (EDS) Octane Elect Plus and EBSD systems. Both the EBSD camera and the EDS detector were controlled by the TEAM software version 4.6.1. The accelerating voltage was 30 kV with the electron beam current of 32 nA. The sample was mounted onto a stage 70° pre-tilted toward the EBSD camera. The EBSD data are processed with MTEX software to acquire the Euler angles with Bunge’s convention (Mainprice et al. 2011).

Results

Raman polarizability tensor

The Raman polarizability tensor is fitted based on Eq. 11 using the X-cut quartz wafer that is cut parallel to the a and c-axes, so that a* is the normal vector to the cut surface. The Raman intensities were obtained every 5 degrees using the sample rotation method. The 10× objective was used here with numerical aperture (NA) being 0.25. In total, there are 72 sets of Raman spectra at different rotation angles (see results in Figs. 3 and 4). The fitted components of Raman polarizability tensor in Table 1 show that for the totally symmetric A₁ mode, the 464 cm⁻¹ band polarizability tensor is nearly isotropic with a/b = 1.0117 ± 0.0008. This isotropic property makes 464 cm⁻¹ band the least sensitive to the crystallographic orientation. Its intensity is only affected by the birefringence effect. Thus, it is ideal as the scaling reference for the other Raman band intensities to determine the crystallographic orientation. The polarizability tensor of the 206 cm⁻¹ band is slightly anisotropic with a/b = 0.9596 ± 0.0008. The polarization components of the 360 cm⁻¹ and 1080 cm⁻¹ bands are negative, i.e., a/b < 0. The fitted birefringence parameter $\chi$ is between 0.251 $\pi$ and 0.255 $\pi$ (the apparent phase shift is 2 $\chi$, which is between 0.502 $\pi$ and 0.510 $\pi$). This is consistent with the theoretically estimated value of $\pi /2$ as described in Kranert et al. (2016a), and experimentally validated in Zheng et al. (2018). This cross-check provides support to the validity of our experiment and the theory.

Fig. 3

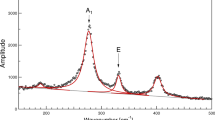
Intensity of Raman spectra in logarithmic scale plotted with respect to the rotation angle and wavenumber. The color illustrates the log₁₀ of Raman intensity. The crystal was rotated using the rotation stage from 0 to 360 degree and the Raman spectra are recorded every 5 degree. Sample rotation method is used here. The totally symmetric A₁ mode Raman bands at 464 cm⁻¹, 206 cm⁻¹ are the strongest and the weaker 360 cm⁻¹ and 1080 cm⁻¹ bands can also be observed. The doubly degenerate E mode Raman bands at around 128 cm⁻¹, 700 cm⁻¹, 265 cm⁻¹ are clearly visible. The Raman band at 1160 cm⁻¹ is measured separately after moving the grating position, thus is not shown here

The fitted polarizability tensor is also compared to the results in She et al. (1971). In She et al. (1971), the sign of a/b and c/d are not obtained. Our results are consistent with the results in She et al. (1971), but have substantial improvement due to: (1) the precise angular rotation angle and high rotation resolution of every 5 degree, (2) the near perfect fit with the measured data as shown in Figs. 3 and 4 the extremely low uncertainties obtained using the bootstrap method. This allows an accurate fit for the crystallographic orientation of quartz grains.

Fig. 4

Normalized intensities of Raman bands of the X-cut quartz wafer cut on the crystallographic c- and a-axes plotted with respect to the polarization direction. The dots are measured Raman data and the black curves are theoretically fitted results based on Eq. 11. The crystallographic c-axis is pointing along the y-axis shown in Fig. 1a. The best-fitted components of Raman polarizability tensor are given in Table 1. The sample rotation method was used. Acquisition time was set to 2 min and each measurement represents four accumulations. In total, 72 Raman spectra were obtained for every 5 degrees rotation

Orientation of quartz cuts

The ST-cut and AT-cut quartz wafers were measured using the 10×, 20×, 50× and 100× objectives and the normalized intensities by the 464 cm⁻¹ band with respect to rotation angle are plotted in Fig. 5. The most important Euler angle is the dip angle $\Phi$, which is shown in Table 2. The orientation $\phi_{1}$ was set at zero by placing the projected c-axis of the quartz wafer along the y-direction on the x–y plane. The dipping angle $\Phi$ was fitted using the method described above. Based on Figs. 5, and 6 and Table 2, the results obtained using 10×, 20×, 50× objectives are very similar, with $\chi /\pi$ all round 0.25, implying that sufficient average depth is reached for the Raman scattering effect. The fitted $\chi /\pi$ result using 100× objective is slightly different at around ca. 0.29 for the ST-cut wafer and ca. 0.34 for the AT-cut wafer, implying that the average depth of the Raman scattering is not sufficient (Kranert et al. 2016a). The best-fitted $\Phi$ angle increases as the numerical aperture increases from 0.25 (20×), 0.75 (50× ) to 0.90 (100×). This is caused by the z-polarization effect when objectives with high numerical aperture is used. The uncertainty due to z-polarization effect is discussed in detail in the Discussions.

Fig. 5

Normalized Raman band intensities of ST-cut quartz wafer. The Raman band intensities are scaled by the 464 cm⁻¹ band. Objectives of 10× (NA = 0.25), 20× (NA = 0.25), 50× (NA = 0.75) and 100× (NA = 0.9) were used to compare the effect of numerical aperture (NA) on the results. It is shown that only the 100× objective has noticeable effect on the result. The fitted dipping angle $\Phi$ and parameter $\chi$ are given in Table 2. The first Euler angle $\phi_{1}$ is set to be zero by placing the quartz wafer’s c-axis perpendicular to the initial polarization direction (x-direction in the figure). The polarizer rotation method was used (see Fig. 1). For each measurement, the acquisition time was 1 min with three accumulations

Table 2 Fitted orientations of the quartz cuts

Fig. 6

Normalized Raman band intensities of AT-cut quartz wafer. The Raman band intensities are scaled by the 464 cm⁻¹ band. Objectives of 10× (NA = 0.25), 20× (NA = 0.25), 50× (NA = 0.75) and 100× (NA = 0.9) were used to compare the effect of numerical aperture (NA) on the results. It is shown that only the 100× objective has noticeable effect on the result. The fitted dipping angle $\Phi$ and parameter $\chi$ are given in Table 2. The first Euler angle $\phi_{1}$ is set to be zero by placing the quartz wafer’s c-axis perpendicular to the initial polarization direction (x-direction in the figure). The polarizer rotation method was used (see Fig. 1). For each measurement, the acquisition time was 1 min with three accumulations

For the two manually cut quartz plate, the results are consistent with the applied cutting angle. The results are shown in Fig. 7. For manual cut 1, whose plane is perpendicular to the c-axis, the best-fitted $\Phi$ is around 1.5 degrees, which is within the uncertainty range of the cutting angle (estimated ca. 2 degrees). For manual cut 2, the normal of its plane is oriented 50 degrees from the c-axis, the best-fitted $\Phi$ is 49.2 ± 0.4 degrees, which is also well within the uncertainty range of the cutting angle. The fitted $\chi /\pi$ is rather low for manual cut 1, ca. 0.03 ± 0.02, which is due to the near isotropic optical property when the cut is nearly perpendicular to the c-axis, i.e., almost no birefringence occurred. For the manual cut 2, the fitted $\chi /\pi$ is around 0.253 ± 0.004, which implies that the Raman scattering depth is sufficient so that it approaches its theoretical limit of 0.25.

Fig. 7

Normalized Raman band intensities of the two manually cut quartz plates, one is cut perpendicular to the c-axis and the other’s normal vector is cut at around 50 degrees to the c-axis. The left insets show the cutting plane with respect to the quartz crystal. The 20 × objective was used for measuring the Raman intensities. The plotted Raman intensities are scaled by the 464 cm⁻¹ band intensity. The polarizer rotation method was used (see Fig. 1). For each measurement, the acquisition time was 1 min with three accumulations

Precision of azimuth angle

The precision of the determined azimuthal angle ($\phi_{1}$) of the c-axis is systematically tested. First, a ST-cut quartz wafer is placed on the rotation stage (see Fig. 1a and b) and the azimuth angle $\phi_{1}$ is measured with Raman spectroscopy using the polarizer rotation method described above. Subsequently, the quartz wafer is rotated counter-clockwise every 30 degrees on the rotation stage, and after each rotation the azimuth angle $\phi_{1}$ is re-measured. The applied rotation angle is compared with the measured rotation angle. The comparison results are shown in Fig. 8. It is demonstrated that the root mean square deviation (RMSD) between the measured and applied rotation angle is within 0.25 degrees. Considering the fact that the applied rotation also has uncertainty (estimated on the level of 0.1 degrees) due to manual handling of the rotation stage and machine error on the scale of the rotation stage, the extremely good consistency between the two sets of angles proves that Raman spectroscopy can provide very precise and more importantly self-consistent measure of the azimuth angle of the c-axis.

Fig. 8

Precision test of the azimuth angle $\phi_{1}$. The x-axis shows the applied sample rotation angle on the ST-cut quartz. Rotation is performed using the rotation stage every 30 degrees. The y-axis shows the measured rotation angle ($\phi_{1}$) using polarizer rotation method. The root mean square deviation (RMSD) between the two sets of results is ca. 0.25 degrees. For each measurement, the acquisition time was 1 min with three accumulations

Quartz inclusion orientation compared to EBSD

Cross validation of the determined crystallographic orientation is performed with the electron backscatter diffraction (EBSD) technique. A sample from an eclogite is used that represents a quenched deformational melt from which the eclogite-facies minerals formed directly at the given ambient high pressure at the seismic event (John and Schenk 2006; Pollok et al. 2014). The sample contains garnet with pressurized quartz inclusions. The thin-section is polished and is ca. 30 $\mu m$ thick. We have measured five exposed quartz inclusions and two entrapped inclusions. The crystallographic orientation of the five exposed quartz inclusions are compared to the EBSD results. The results are shown in Table 3 and Fig. 9. In general, the results from Raman spectroscopy and EBSD technique match very well with difference mostly less than 2 to 3 degrees. There are occasionally larger deviations, e.g., inclusion #3 and #5 with difference higher than 5 degrees.

Fig. 9

Normalized Raman intensities of quartz inclusions in eclogite sample from Zambia. a–e show the results of exposed quartz inclusions and the microphotographs are taken with reflected light. f, g are fully entrapped inclusions and the microphotographs were taken with transmitted light. The c-axis is shown by the yellow arrow on the microphotographs. The best-fitted Euler angles are given in Table 3

Two fully entrapped quartz inclusions were measured (Fig. 9f and g). The inclusion #6 has its c-axis nearly parallel to the x–y plane, while the inclusion #7 has its c-axis nearly parallel to the z-axis. The uncertainty of the azimuthal angle $\phi_{1}$ of inclusion #7 is high (ca. 4 degree) because the c-axis is nearly vertical and the Raman band intensities are not sensitive to the polarization direction.

Discussions and geological implications

Advantage and disadvantage of the two rotation methods

The two rotation methods, i.e., sample and polarizer rotation (see Fig. 1), each have advantages and disadvantages. The advantage of the sample rotation method is that the polarization direction is not changed due to the fixed polarizer, thus the measured Raman intensity is not affected by the sensitivity of spectrometer to the polarization orientation of the laser beam. However, the disadvantage is that by rotating the stage, the focus of the objective may be shifted, which becomes problematic for measuring tiny inclusions. The advantage of the polarizer rotation method is that the focus of the beam is always fixed so that it is ideal for measuring tiny inclusions. The disadvantage is that by rotating the circular polarizer, the recorded Raman intensity is dependent on the orientation of the elliptically polarized light after the beam passes through the quarter waveplate on the circular polarizer. In other words, the Raman intensities become affected by the directional sensitivity of spectrometer. Therefore, we chose the sample rotation method to perform measurement on the high-quality quartz wafer to fit the Raman polarizability tensor. We applied the polarizer rotation method on tiny inclusions and other quartz cuts so that the laser position is always stable during the rotation of the circular polarizer. Due to the sensitivity of polarization direction, scaling of the Raman band intensities is necessary. In this case, it was performed using the dominant 464 cm⁻¹ Raman band (see e.g. Eq. 12).

Uncertainties and limitations

Z-polarization effect

One important issue introduced using objectives with high magnification is that the z-polarization parallel to the direction of the laser beam may become effective, and its significance strongly depends on the numerical aperture of the objective (Mossbrucker and Grotjohn 1996; Saito 2007). The reason is that the laser’s travel path is not perfectly parallel to the z-axis in practice, but form a “cone” shape. The numerical aperture is defined as ${\text{NA}} = n{\text{ sin}}\left( {\upgamma } \right)$, where $n$ is the refractory index and ${ \gamma }$ is the half angle of the cone. Therefore, some light will travel at an angle to the z-axis depending on the numerical aperture (NA) of the objective. Generally, for higher magnification objectives, the numerical aperture is higher. In this case, the electric field of the incident laser in z-direction will trigger Raman scattering, which leads to a deviation of the Raman intensity from the predicted value based on Eq. 10.

In this study, we have tested 10× (NA = 0.25), 20× (NA = 0.25), 50× (NA = 0.75) and 100× (NA = 0.90) objectives on the ST-cut quartz wafer. It is shown that a small effect on the fitted dipping angle $\Phi$ is present when using 50× (NA = 0.75) and 100× (NA = 0.9). Particularly for the 100× objective, the fitted $\Phi$ is different from the correct angle by about 1–2 degrees and the best-fitted intensity v.s. orientation curves are not perfectly consistent with the measured data (Fig. 5d). The fitted $\Phi$ with ca. 1 to 2 degrees deviation from the correct value may be potentially acceptable depending on the precision requirement of specific applications. In some geological applications, e.g., measurement on small inclusions, it is often not possible to use low magnification objectives to collect sufficient Raman signal on inclusions with diameter less than, e.g., 2–3 ${\mu m}$. In this case, a compromise between sufficiently high magnification for good signal and sufficiently low numerical aperture to avoid by z-polarization needs to be chosen. In this study, we found that the 50× objective (NA = 0.75) to be a reasonable compromise to effectively suppress the z-polarization effect while keeping a sufficiently high magnification for inclusion measurement.

Rotation resolution of polarizer

The resolution of rotation is a critical factor in determining the precision of the fitted crystallographic orientation. Here, the rotation resolution is tested systematically at 10, 20, 30, 40, 60, 90, and 120 degrees interval on the ST-cut quartz wafer. The results are shown in Table 4. It is demonstrated that for rotation resolution below 40 degrees, the regression is still robust and the fitted dipping angle $\Phi$ of the c-axis and birefringence parameter $\chi$ are both correct. Above 60 degrees rotation resolution, these fitted parameters become biased and the results are not reliable. Therefore, it is demonstrated that the rotation angle needs to be less than at least 30 degrees, ideally between 10 and 20 degrees to keep a balance between the time expense and the precision of the results.

Table 3 Fitted inclusion orientation data using Raman spectroscopy and EBSD technique

Choice of Raman bands

In this study, we have attempted to fit the crystallographic orientation using four totally symmetric A₁ mode and three doubly degenerate E mode Raman bands. In some specific cases, e.g., when measuring small inclusions entrapped in a host, some Raman bands may not be measurable either due to their low intensities or because they are overwhelmed by the strong Raman bands from the host mineral. Therefore, we have tested the possibility of using a limited number of Raman bands to obtain the crystallographic orientation.

The 464 cm⁻¹ band must be used as it is the most dominant peak and is least affected by the crystallographic orientation due to its near-isotropic Raman polarizability tensor. In this study, we chose it as a scale or reference for the other bands. The other six bands, 206, 360, 1080, 128, 700, 1160 cm⁻¹ are chosen in various combinations. In Table 5, we show the fitted Euler angles of the ST-cut quartz wafer based on different combination of Raman bands. The tick symbols indicate which Raman bands are used for fitting the crystallographic orientation.

Table 4 Fitted dipping angle $\Phi$ and the third Euler angle $\phi_{2}$ as a function of rotation resolution in degrees

It is shown that only using the 206 cm⁻¹ band leads to an erroneous result. This is because the Raman polarizability tensor of the 206 cm⁻¹ band is extremely similar to that of the 464 cm⁻¹ band (see Table 1), which serves as a scale. Therefore, the ratio between 206 and 464 cm⁻¹ bands is not sensitive to the crystallographic orientation. The fitted results are significantly improved when the 128 cm⁻¹ band is added to the regression.

Naturally, the best-fitted results are obtained when all the Raman bands are used for the regression. However, above three Raman bands, the benefit of adding more Raman bands is small. The fitting improvement from using four Raman bands (128, 206, 1080 or 1160 cm⁻¹) to five Raman bands (128, 206, 1080, 1160 and 700 cm⁻¹) is not significant. Therefore, in case it is not possible to obtain all the Raman bands, the least number of Raman bands used should be two to three, e.g., including the strong 128 cm⁻¹ and 206 cm⁻¹ bands plus one more band if measurable. It is also demonstrated in Table 5 that a reasonable result of $\Phi$ ca. 46.2 ± 0.1 degree for the ST-cut can be fitted only using the 128 cm⁻¹ and 206 cm⁻¹ bands, and the difference to the correct dipping angle (47.3 degrees) is only around 1 degree. This is potentially already satisfactory for many practical applications.

Direction of c-axis

The Raman intensity will be identical if the c-axis is mirrored on the x–y plane, i.e., the plane forming the microscopy stage. Therefore, it is not straightforward to determine whether the c-axis is pointing upward or downward from the x–y plane after fixing the azimuth angle $\phi_{1}$. In other word, the determined dipping angle $\Phi$ can also be $180 - \Phi$ and the resulting Raman intensity with respect to $\theta$ will be exactly the same. There is no simple method to determine it, as the laser beam is perpendicular to the sample surface. One approach is to tilt the sample on the x–y plane and observe whether the angle $\Phi$ decreases or increases. Here, an experiment is done on the 50 degrees quartz cut. The measured $\Phi$ angle is ca. 49.2 degrees when the sample is placed flat on the stage. The sample is then placed on a plastic wedge. After measuring the angle $\Phi$, the sample is flipped so that the c-axis is also flipped to the other side to obtain a new $\Phi$. It is found that before the flip, the angle $\Phi$ is 38.8 degrees and after the flip, the $\Phi$ increases to 63.8 degrees. Therefore, the direction of the c-axis can be found as shown in Fig. 10. A schematic diagram is given in Fig. 10 to illustrate the determination process. A faster method has been recently developed in Ilchenko et al. (2019), where an additional objective is placed ca. 45 degrees to the sample surface to provide an inclined laser propagation direction. However, this requires a change in the optical path and is not possible with a standard Raman spectroscopy.

Fig. 10

Schematic diagram showing how to differentiate c-axis up and c-axis down. In a, the quartz plate is cut with $\Phi$ being 50 degrees. If the c-axis is mirrored on the x–y plane as denoted by the transparent axis (c-), identical Raman signal will be obtained. Measuring the quartz plate with vertical laser beam cannot determine whether the c-axis is up (c +) or down (c-). In b, the quartz cut is placed on a plastic wedge and $\Phi$ is again measured to be around 38 degrees (< 50 degrees). In c, the quartz cut is flipped and the $\Phi$ is measured around 64 degrees (> 50 degrees). If the c-axis is down (-) as shown by the transparent c-axis in a, the measured $\Phi$ will be flipped after the identical operations in b and c, i.e., 64 degrees in b and 38 degrees in c

Refraction and reflection on sloped surface

Refraction occurs when the sample surface is not flat. In this case, the measured $\Phi$ becomes the angle between the refracted laser and the c-axis. This results in uncertainty when measuring a sample with its top surface being not flat. An idealized analysis can be done using the Snell’s law assuming the interface between the sample and surrounding material is a tilted plane. The laser always propagates vertically when it arrives at the sample. For a sample with its top surface inclined by an angle $\xi$ from the x–y plane, the bending angle of the laser beam due to refraction is expressed as follows derived from the Snell’s law:

$$\Delta \xi = asin\left( {\frac{{n_{1} }}{{n_{2} }}sin\left( \xi \right)} \right) - \xi$$

(13)

where $n_{1}$ is the refractive index of the surrounding material and $n_{2}$ is the refractive index of the sample. For a tilted sample in the air, $n_{1}$ takes an approximate value of 1. For a quartz plate ($n_{2} = 1.55$) with a tilted slope $\omega = 30^\circ$, the bending angle $\Delta \omega$ of the laser beam is ca. 11.2 degrees. The bending angle can be significantly reduced if the sample is submerged into oil ($n_{1} = 1.51$), so that $\Delta \omega$ reduces to ca. only 0.8 degrees.

The same equation applies to an inclusion entrapped in host mineral. For garnet host ($n_{1} = 1.73$) with a quartz inclusion ($n_{2} = 1.55$), whose upper surface is tilted by an angle $\omega = 30^\circ$, the bending angle due to refraction is ca. $\Delta \omega = 3.9^\circ$. For a flatter surface $\omega = 10^\circ$, the bending angle drops to $\Delta \omega = 1.2^\circ$. This analysis takes simple assumptions that the refractive index is isotropic and the inclusion-host interface is a tilted flat plane. The bending angle increases when the refractive index ratio between the host and inclusion ($n_{1} /n_{2}$) deviates from 1. In natural rocks, the inclusion shape is complicated and the refracted beam path may not be simple. Another potential source of error occurs when the inclusion’s bottom surface is tilted, thus leading to the reflected beam to depart from the incident beam direction. Therefore, care must be taken on irregularly shaped inclusions. The reflection effect is probably the main reason for the small discrepancy between the determined crystallographic orientation with Raman spectroscopy and EBSD technique in Table 3, because the measured inclusions are small and their lower surface is within the garnet host and is often not flat. With this respect, a higher magnification objective is preferred but it also suffers the problem of z-polarized effect discussed before.

Table 5 Fitted Euler angle using different Raman bands for the ST-cut quartz wafer

Geological implications

This study focuses on presenting the Raman polarizability tensor and proposed a framework to determine the crystallographic orientation of small quartz inclusions in other minerals. Here, several potential geological applications and implications can be envisioned.

The technique may potentially promote the application of elastic thermobarometry as there will be no need to polish the thin section, which may lead to a partial or total release of the residual stress (Mazzucchelli et al. 2018; Zhong et al. 2020). It will facilitate future work on this topic because quartz inclusions are anisotropic, thus the determination of their crystallographic orientation is relevant when individual strain components along either c or a-axes are obtained using, e.g., the phonon Grüneisen tensor (Murri et al. 2018) or the deformation potential constants (Briggs and Ramdas 1977). It has been shown by Zhong et al. (2021a) that the residual stress and strain preserved in an inclusion can be correlated to the strain difference between the inclusion and host at entrapment P–T conditions, i.e., the eigenstrain that loads the system to the current stress state (Eshelby 1957; Mura 1987). For a non-spherical quartz inclusion, the preserved residual stress will be affected by the inclusion shape, as well as the relationship between the crystallographic orientation of the inclusion and the host (e.g.,Zhukov and Korsakov 2015; Mazzucchelli et al. 2018; Zhong et al. 2021a). There is currently no experimental measurement on the unit cell parameters of quartz crystal at high P–T conditions simultaneously (see e.g. data obtained in Angel et al. 1997; Carpenter et al. 1998; Raz et al. 2002), but it has been attempted in Alvaro et al. (2020) to extrapolate the individual unit cell parameters to high P–T conditions based on unit cell data obtained at room-T, high-P and room-P, high-T conditions. Because it is not entirely known how large the uncertainty is regarding the extrapolation of individual unit cell parameters to high P–T conditions, we do not perform calculations on elastic barometry as this is beyond the scope of this paper. However, within the scope of elastic thermobarometry, our work of measuring the crystallographic orientation directly using Raman spectroscopy characterizes a step forward for the further development of the technique because the crystallographic orientation can be correlated to the recovered strain/stress components.

The presented method is not restricted to quartz inclusion as the determination of crystallographic orientation of other mineral inclusions follows the same procedure. Apart from elastic thermobarometry, the orientations of mineral inclusions with respect to the host also provide valuable information of the petrological process during the formation of the rock (Hwang et al. 2015; Griffiths et al. 2016). Systematically oriented inclusions, such as apatite and rutile, with respect to, e.g., garnet host may reveal, e.g., exsolution and precipitation processes of Ti or P elements (Axler and Ague 2015). Understanding the crystallographic orientation relationship between inclusion and host requires analytical technique such as EBSD. It has been demonstrated here that it is also possible to measure such data using Raman spectroscopy even for entrapped inclusions, which may expand the depth of the exploration for inclusions. The advantage is that the technique is simple and does not require high-standard polishing as for the application of EBSD. This may be an advantage for the determination of fragile phyllosilicates minerals such as mica that is difficult to index by EBSD after polishing (e.g., see Charoensawan et al. 2021). It is also possible to perform Raman mapping to retrieve the spatial variation of the crystallographic orientation of sub-grains. For example, the Rhynie chert is mapped by Fries and Steele (2010), where the spatial variation of the 128 cm⁻¹ Raman band intensity is ascribed to the variation of crystallographic orientation.

Conclusion

In this study, we measured the Raman polarizability tensor of quartz crystal with high precision and succeeded in recovering the crystallographic orientation of arbitrarily orientated quartz grains. The method requires rotating the relative orientation between the polarization direction of the laser and the quartz sample. Two methods, i.e., sample rotation and polarizer rotation, are described. The measured crystallographic orientations of quartz wafers and manually cut quartz plates show very high precision with error less than 0.25 degrees. Quartz inclusions from natural eclogite sample were measured to show the potential of the method and the exposed quartz inclusions are compared to results obtained using EBSD technique. In general, the determination of crystallographic orientation using Raman spectroscopy is proven to be very robust and can be used in petrological studies that require understanding of the lattice orientation of rock forming minerals. It has the potential to be applied in Raman elastic thermobarometry and will avoid the trouble of polishing the thin-section and transferring the thin-section to a different analytical tool for orientation measurement.

Appendices

Appendix

A1. Coefficients for Raman intensity

The Raman intensity is proportional to the following formula:

$$I_{s} \propto \left| {\left[ {C_{1} \cos \left( \theta \right)^{2} + C_{2} \sin \left( \theta \right)^{2} + C_{3} \sin \left( {2\theta } \right)} \right]^{2} } \right|$$

The coefficients $C_{i}$ are functions of the Euler angles and the components of the Raman polarizability tensor. For the totally symmetric A₁ mode, we have:

$$C_{1} = a\cos^{2} \phi_{1} + \sin^{2} \phi_{1} \left( {a\cos^{2} \Phi + b\sin^{2} \Phi } \right)e^{2i\chi }$$

$$C_{2} = a\sin^{2} \phi_{1} + \cos^{2} \phi_{1} \left( {a\cos^{2} \Phi + b\sin^{2} \Phi } \right)e^{2i\chi }$$

$$C_{3} = \frac{1}{2}\sin 2\phi_{1} \left[ {a - \left( {a\cos^{2} \Phi + b\sin^{2} \Phi } \right)e^{2i\chi } } \right]$$

It is noticed that the intensity does not depend on the second Z rotation angle $\phi_{2}$. For the doubly degenerate E mode, we have two components. For the E(x) mode:

$$C_{1} = c\cos^{2} \phi_{1} \cos 2\phi_{2} - \sin 2\phi_{1} e^{i\chi } \left( {c\cos \Phi \sin 2\phi_{2} + d\sin \Phi \sin \phi_{2} } \right) - \sin^{2} \phi_{1} e^{2i\chi } \left( {c\cos^{2} \Phi \cos 2\phi_{2} + d\sin 2\Phi \cos \phi_{2} } \right)$$

$$C_{2} = c\sin^{2} \phi_{1} \,\cos 2\phi_{2} + \sin 2\phi_{1} e^{i\chi } \left( {c\cos \Phi \sin 2\phi_{2} + d\sin \Phi \sin \phi_{2} } \right) - \cos^{2} \phi_{1} e^{2i\chi } \left( {c\cos^{2} \Phi \cos 2\phi_{2} + d\sin 2\Phi \cos \phi_{2} } \right)$$

$$C_{3} = \frac{c}{2}\sin 2\phi_{1} \cos 2\phi_{2} + \cos 2\phi_{1} e^{i\chi } \left( {c\cos \Phi \sin 2\phi_{2} + d\sin \Phi \sin \phi_{2} } \right) + \sin 2\phi_{1} \cos \Phi e^{2i\chi } \left( {\frac{c}{2}\cos \Phi \cos 2\phi_{2} + d\sin \Phi \cos \phi_{2} } \right)$$

For the E(y) mode:

$$C_{1} = c\cos^{2} \phi_{1} \sin 2\phi_{2} + \sin 2\phi_{1} e^{i\chi } \left( {c\cos \Phi \cos 2\phi_{2} - d\sin \Phi \cos \phi_{2} } \right) - \sin^{2} \phi_{1} e^{2i\chi } \left( {c\cos^{2} \Phi \sin 2\phi_{2} - d\sin 2\Phi \sin \phi_{2} } \right)$$

$$C_{2} = c\sin^{2} \phi_{1} \sin 2\phi_{2} - \sin 2\phi_{1} e^{i\chi } \left( {c\cos \Phi \cos 2\phi_{2} - d\sin \Phi \cos \phi_{2} } \right) - \cos^{2} \phi_{1} e^{2i\chi } \left( {c\cos^{2} \Phi \sin 2\phi_{2} - d\sin 2\Phi \sin \phi_{2} } \right)$$

$$C_{3} = \frac{c}{2}\sin 2\phi_{1} \sin 2\phi_{2} - \cos 2\phi_{1} e^{i\chi } \left( {c\cos \Phi \cos 2\phi_{2} - d\sin \Phi \cos \phi_{2} } \right) + \sin 2\phi_{1} \cos \Phi e^{2i\chi } \left( {\frac{c}{2}\cos \Phi \sin 2\phi_{2} - d\sin \Phi \sin \phi_{2} } \right)$$

Note that for the E mode, two $I_{x}$ and $I_{y}$ need to be separately calculated and the corresponding intensities are summed up to obtain the total Raman intensity.

A2. Steps in calculating Raman intensity and numerical example

A few steps are outlined here that guide readers to calculate the Raman intensity using the method described in this paper. A numerical example is also given at the end.

(1) Take the unrotated Raman polarizability tensor ${\varvec{\alpha}}_{{\varvec{U}}}$, either the A₁ or E model, into the equation for the active Euler rotation: ${\varvec{R}}_{{{\varvec{Z}}1}} {\varvec{R}}_{{\varvec{X}}} {\varvec{R}}_{{{\varvec{Z}}2}} {\varvec{\alpha}}_{{\varvec{U}}} {\varvec{R}}_{{{\varvec{Z}}2}}^{{\varvec{T}}} {\varvec{R}}_{{\varvec{X}}}^{{\varvec{T}}} {\varvec{R}}_{{{\varvec{Z}}1}}^{{\varvec{T}}}$ to get a 3-by-3 rotated Raman polarizability tensor and only take its first 2-by-2 part to form a 2-D matrix ${\varvec{\alpha}}$ by neglecting all the z-components.

(2) Apply the rotated Jones matrix ${\varvec{J}} = {\varvec{R}}_{{{\varvec{Z}}1}} \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & {e^{i\chi } } \\ \end{array} } \right]{\varvec{R}}_{{{\varvec{Z}}1}}^{{\varvec{T}}}$ to the rotated Raman polarizability tensor ${\varvec{\alpha}}$ to get ${\varvec{J}} \cdot {\varvec{\alpha}} \cdot {\varvec{J}}$. Only take the first 2-by-2 components of the rotation matrix ${\varvec{R}}_{{{\varvec{Z}}1}}$.

(3) Apply the incident and scattered electric field vector to the outcome of step 2 and calculate the Raman intensity:${ }I_{s} \propto \left| {{\varvec{e}}_{{\varvec{i}}} \cdot {\varvec{J}} \cdot {\varvec{\alpha}} \cdot {\varvec{J}} \cdot {\varvec{e}}_{{\varvec{s}}} } \right|^{2}$. A complex number is present in the absolute symbol. The absolute value of a complex number is defined as the distance between the origin (0, 0) and the point (a, b) in the complex plane, i.e., $\left| {a + bi} \right| = \sqrt {a^{2} + b^{2} }$.

It is also possible to simply calculate $C_{1}$, $C_{2}$ and $C_{3}$ using the Euler angles and the Raman polarizability tensor components and substitute them into Eq. 10. The same numerical result is expected as can be checked.

A numerical example is given. In the sample, we assume a crystal with an unrotated Raman polarizability tensor:

$${\varvec{\alpha}}_{{\varvec{A}}} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \\ \end{array} } \right]$$

The crystal orientation is described by the three Euler angles: $\phi_{1} = 40^\circ$, $\Phi = 30^\circ$ and $\phi_{2} = 50^\circ$ and birefringence factor $\chi = 0.25\pi$. We may calculate the expected Raman band intensity following the steps given. After step 1, we obtain the rotated 2-D polarizability tensor $\alpha$ is as follows:

$${\varvec{\alpha}} = \left[ {\begin{array}{*{20}c} {1.103} & { - 0.123} \\ { - 0.123} & {1.147} \\ \end{array} } \right]$$

In step 2, we calculate the rotated Jones matrix:

$${\varvec{J}} = \left[ {\begin{array}{*{20}c} {0.879 + 0.292i} & {0.144 - 0.348i} \\ {0.144 - 0.348i} & {0.828 + 0.415i} \\ \end{array} } \right]$$

Assume the angle of the polarizer to be $\theta = 60^\circ$. In step 3, we obtain the electric field vector: ${\varvec{e}}_{{\varvec{i}}} = {\varvec{e}}_{{\varvec{s}}} = \left[ {\begin{array}{*{20}c} {0.500} & {0.866} \\ \end{array} } \right]$. Multiplying them together we obtain $I_{s} \propto \left| {{\varvec{e}}_{{\varvec{i}}} \cdot {\varvec{J}} \cdot {\varvec{\alpha}} \cdot {\varvec{J}} \cdot {\varvec{e}}_{{\varvec{s}}} } \right|^{2} = 0.801$, which is the expected Raman intensity without a pre-factor. By rotating the polarizer angle $\theta$, the intensity will vary systematically.

The same results can be obtained by calculating $C_{1} = 0.587 + 0.517i$, $C_{2} = 0.413 + 0.734i$ and $C_{3} = 0.492 - 0.616i$. We obtain the same Raman intensity by performing the calculation $I_{s} \propto \left| {\left[ {C_{1} \cos \left( \theta \right)^{2} + C_{2} \sin \left( \theta \right)^{2} + C_{3} {\text{sin}}\left( {2\theta } \right)} \right]^{2} } \right| = 0.801$. Note that the square operation is inside the absolute symbol.

For the E mode, given the same Euler angle and taking the unrotated Raman polarizability tensor as follows:

$${\varvec{\alpha}}_{{{\varvec{Ex}}}} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & { - 1} & 2 \\ 0 & 2 & 0 \\ \end{array} } \right]$$

$${\varvec{\alpha}}_{{{\varvec{Ey}}}} = \left[ {\begin{array}{*{20}c} 0 & { - 1} & { - 2} \\ { - 1} & 0 & 0 \\ { - 2} & 0 & 0 \\ \end{array} } \right]$$

, we may calculate the Raman band intensity for the two E modes $I_{Ex} = 0.725$ and $I_{Ey} = 1.697$, which sums up to 2.422 as the final E mode intensity. The readers may follow the steps and this example to test their calculation.

A3. Examples

To better visualize the axes rotation, two examples are given here as shown in Fig. A1. A quartz crystal is placed under the microscope with two different orientations and measured with Raman spectroscopy. Initially, the Cartesian z-axis is parallel to the crystallographic c-axis and the Cartesian x-axis is parallel to the crystallographic a-axis. It is shown that after three rotations following the Z–X–Z order, the initial sample reference frame is rotated into the reference frame of the crystal. The measured Raman band intensities are given in the supplementary data. A MATLAB script is provided to recover the crystallographic orientation of the quartz crystal.

Fig. A1 Two examples of a quartz crystal oriented differently and measured with Raman spectroscopy. The Bunge convention is used (Z–X–Z rotation order from the initial sample reference frame into crystal reference frame). The first example shows a near horizontally orientation c-axis, where the quartz crystal is placed on the stage. The second example shows a slightly tilted c-axis from the x–y plane fixed using plasticine. The rotation procedures are shown.