Abstract
The unavoidable interaction of an open quantum system with its surrounding environment may follow non-Markovian dynamics behavior, which causes its memory effects to play a key role in many quantum technologies. In this work, we first consider the dynamics control of a spin-1/2 system that simultaneously interacts with two magnets. Subsequently, we study in detail the evolution of a classically driven spin-1/2 system that is coupled with a magnet. Two dynamical crossovers of the spin system, namely, from Markovian dynamics to non-Markovian dynamics and from no-speedup evolution to speedup evolution, can be controlled in these two models. Slightly different from the previous quantum speedup scenarios with controllable non-Markovianity, the stronger non-Markovianity does not necessarily lead to the quantum speedup dynamics process of the spin system in our spin-magnet schemes.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
In general, it is impossible to isolate any realistic quantum system from the surrounding environment completely. Thus, the understanding and control of the dynamics of an open quantum system is a challenging task in almost every area of quantum physics. The dynamics of an open quantum system has been described extensively by the Born–Markov approximation [1–3], which assumes memoryless dynamics of an open quantum system, with the information continuously flowing to its environment. Furthermore, a Markovian process can be described by a dynamical semigroup with a time-independent Lindbald generator [4]. However, the Born–Markov approximation fails in the presence of memory effects; for example, those resulting from strong system–environment coupling [5, 6]. Quantum devices exhibit non-Markovian rather than Markovian dynamics behavior when an information backflow from the environment to the system exists.
Non-Markovian dynamics behavior may be more advantageous than Markovian dynamics behavior owing to memory effects. In recent years, the exploration of the non-Markovian memory effects on quantum systems has attracted considerable attention, both theoretically [7–18] and experimentally [19–26]. Interestingly, the non-Markovian effects not only suppress the decay of the coherence or entanglement of quantum systems [27–29], but also offer a new perspective for applications in quantum metrology [30] and the quantum speed limit time (QSLT) [31–44]. Moreover, to the best of our knowledge, owing to the memory effects and the ability for recovering quantum features in the non-Markovian dynamics process, the robustness of quantum simulators and computers [45, 46] as well as the higher precision in estimating the parameters of quantum technology [30], perfect processing is possible. Thus, controlling the dynamics of an open quantum system; in particular, manipulating the non-Markovian effects and improving the quantum dynamical speed is extremely significant for reliable quantum information processing [47–52].
At present, many approaches for characterizing non-Markovianity, which can claim non-Markovian evolution if nonzero non-Markovianity is detected, have been established by including the trace distance [11], bipartite entanglement [14, 53], quantum Fisher information [22, 54], and temporal steering [55]. Based on these measures of non-Markovianity, numerous schemes have been investigated to manipulate the non-Markovian dynamics behavior and to achieve the quantum speedup of open systems. Certain theoretical circumstances under which non-Markovian behavior of the system may occur, such as strong system–environment coupling, hierarchical environments, and initial system–environment correlations, have frequently been mentioned. Although the non-Markovianity of the environment has also been manipulated in several experiments, these were often limited to certain physical systems; for example, a photon in a linear optical system [19, 21], the adjacent nuclear spins of a nitrogen-vacancy center in diamond [22], or a weakly driven optical cavity QED system [34]. Therefore, it is also necessary and highly significant to continue seeking a new physical system to design an operational and experimental implementation for controllable non-Markovian behavior.
The Curie–Weiss model (spin-magnet model) [56, 57] describes an interaction between the z component  of a spin-1/2 system and a magnet as the role of the environment. This basic spin-magnet model actually conforms to the form of the Markovian dynamics master equation. In this work, to acquire the information backflow from the magnetic environment and the non-Markovian dynamics behavior of the spin-1/2 system, we demonstrate two new models based on the basic spin-magnet model by adding a second magnet and applying a static Zeeman field on the spin-1/2 system. Following the initial attempts in [56, 58], we first study the evolution of a spin-1/2 system that simultaneously interacts with two magnets in detail, by attempting to couple a different spin component (model A) and the affected spin-1/2 system with a static Zeeman field (model B). Two dynamical crossovers of the spin system, namely those from Markovian dynamics to non-Markovian dynamics and from no-speedup evolution to speedup evolution, can be controlled in the above two models. In model A, when the spin system couples to two independent magnets with two noncommutative interaction Hamiltonians, new non-Markovian dynamics and quantum speedup of the open system evolution can be achieved. In model B, the non-Markovian dynamics behavior and corresponding speedup dynamics of the evolution process can be achieved by applying a static Zeeman field on the spin system in the case of the spin Hamiltonian and interaction Hamiltonian satisfying the noncommutative relationship. Furthermore, it is interesting to note that, when an induction of a static Zeeman field is along the component
of a spin-1/2 system and a magnet as the role of the environment. This basic spin-magnet model actually conforms to the form of the Markovian dynamics master equation. In this work, to acquire the information backflow from the magnetic environment and the non-Markovian dynamics behavior of the spin-1/2 system, we demonstrate two new models based on the basic spin-magnet model by adding a second magnet and applying a static Zeeman field on the spin-1/2 system. Following the initial attempts in [56, 58], we first study the evolution of a spin-1/2 system that simultaneously interacts with two magnets in detail, by attempting to couple a different spin component (model A) and the affected spin-1/2 system with a static Zeeman field (model B). Two dynamical crossovers of the spin system, namely those from Markovian dynamics to non-Markovian dynamics and from no-speedup evolution to speedup evolution, can be controlled in the above two models. In model A, when the spin system couples to two independent magnets with two noncommutative interaction Hamiltonians, new non-Markovian dynamics and quantum speedup of the open system evolution can be achieved. In model B, the non-Markovian dynamics behavior and corresponding speedup dynamics of the evolution process can be achieved by applying a static Zeeman field on the spin system in the case of the spin Hamiltonian and interaction Hamiltonian satisfying the noncommutative relationship. Furthermore, it is interesting to note that, when an induction of a static Zeeman field is along the component  (or
(or 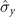 ) of the spin, and causes the magnet to couple with the component
) of the spin, and causes the magnet to couple with the component 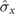 of the spin, substantially greater non-Markovianity of the dynamics process can be obtained. Furthermore, compared to the analysis of non-Markovianity and the QSLT in our considered spin-magnet models, it can be clearly illustrated that the stronger non-Markovianity does not necessarily lead to a quantum speedup dynamics process of the spin system. Thus, the fact that the memory effect may induce a speedup dynamics process can only be established in certain physical systems.
of the spin, substantially greater non-Markovianity of the dynamics process can be obtained. Furthermore, compared to the analysis of non-Markovianity and the QSLT in our considered spin-magnet models, it can be clearly illustrated that the stronger non-Markovianity does not necessarily lead to a quantum speedup dynamics process of the spin system. Thus, the fact that the memory effect may induce a speedup dynamics process can only be established in certain physical systems.
2. Methods: spin-magnet models and dynamics of spin-1/2 system
We first consider the Curie–Weiss model [56, 57] in which a spin-1/2 particle S (qubit) interacts with a magnetic environment B that is composed of N spin-1/2 systems. For simplicity, we consider the free Hamiltonian of the magnet HB
= 0. The free Hamiltonian of system HS
and the interacting Hamiltonian HI
are commutative: [HS
, HI
] = 0. The interacting Hamiltonian, which describes the coupling of the z component 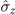 of a spin-1/2 system by a magnet, is expressed as
of a spin-1/2 system by a magnet, is expressed as
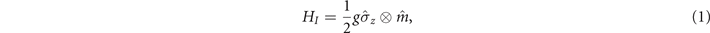
where g is the coupling strength between the system and magnet. Moreover,  is the magnetization operator of the magnet:
is the magnetization operator of the magnet:

where mk
= −N + 2k is the magnetization for k = 0, ..., N and Πk
is the projector onto the subspaces with a magnetization mk
. It is well known that this model is completely solvable by the master equation and it corresponds to the purely dephasing model. Without loss of generality, by assuming the Gaussian distribution of the magnet  , where λ is the standard deviation, the dynamics of the spin system can be expressed by [59, 60]
, where λ is the standard deviation, the dynamics of the spin system can be expressed by [59, 60]
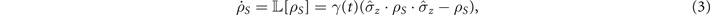
with the time-dependent decay rate γ(t) = λ2 g2 t in the Gaussian case. For any t > 0, the time-dependent decay rate always satisfies γ(t) > 0. According to [60, 61], although the decay rate is time dependent, the dynamic process of the spin will conform to Markovianity in this spin-magnet model. To change the dynamics from Markovian to non-Markovian behavior, we construct two new models based on the original spin-magnet model by adding a second magnet or applying a static Zeeman field on the spin system, as illustrated in figure 1. In the following, we mainly present the calculation of the spin system dynamics under these two proposed models.
Figure 1. Schematic representation. Two schemes are provided by modifying the spin-magnet model to acquire the non-Markovian dynamics behavior of the spin system.
Download figure:
Standard image High-resolution image2.1. Model A: addition of a new magnet
We consider the evolution of a spin-1/2 system S (qubit) that simultaneously interacts with two magnets (B1 and B2). Here, two states (|↑⟩S and |↓⟩S ) of double degenerate energy levels of a spin-1/2 system are chosen to describe two complete basis vectors of this qubit system. Now, the free Hamiltonian HS of the spin-1/2 system is a constant one. Both magnets follow the Gaussian distribution with standard deviations that are labeled as λ1 and λ2, respectively. These two Gaussian distributions formally correspond to the asymptotic limit of two magnets described by two microcanonical ensembles. For simplicity, we consider the free Hamiltonians of these two magnets to vanish: HB1 = 0 and HB2 = 0. The interaction Hamiltonians between the spin and the two magnets are expressed as
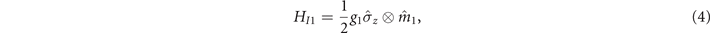
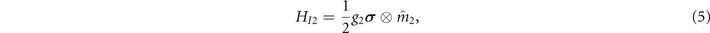
where g1 and g2 are the coupling strengths between the system and two magnets, respectively. Furthermore, 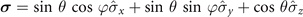 is the operator of the spin system, which is related to two direction angles θ ∈ [0, π] and φ ∈ [0, 2π]. The free Hamiltonian of the system is commutative with the interaction Hamiltonians, [HS
, HI1 + HI2] = 0.
is the operator of the spin system, which is related to two direction angles θ ∈ [0, π] and φ ∈ [0, 2π]. The free Hamiltonian of the system is commutative with the interaction Hamiltonians, [HS
, HI1 + HI2] = 0.
In the case of g2 = 0, model A is the Curie–Weiss model (spin-magnet model), and the spin system dynamics is Markovian. To solve the spin system dynamics precisely, it is necessary to focus on the effects of the added second magnet. According to [61], only under restrictive conditions (the free Hamiltonian of the system is commutative with the interaction Hamiltonians, and any two interaction Hamiltonians are commutative: [HIi , HIj ] = 0) can the dynamical generator of the open system that is coupled with multiple magnetic environments be naively solved by adding the generators to every magnetic environment. However, in our considered spin–magnet model, it is worth noting that [HI1, HI2] = 0 is only satisfied under the condition θ = 0, π. In general, [HI1, HI2] ≠ 0 is selected to analyze and calculate the spin system dynamics. Therefore, the calculation of the dynamics of the open system under model A cannot be simply solved by adding the generators to the master equation. In the following, we first present the exact evolution of the spin system that is derived microscopically.
The initial state of the total system is expressed as 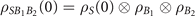 , where two magnetic environments are selected as a classical mixture of different magnetizations:
, where two magnetic environments are selected as a classical mixture of different magnetizations:
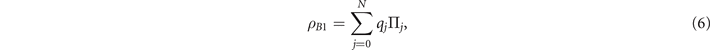

in which ![${q}_{j}\enspace \mathrm{Tr}[{{\Pi}}_{j}]=\mathrm{Tr}[{\rho }_{{B}_{1}}{{\Pi}}_{j}]=p({m}_{1,j})$](https://content.cld.iop.org/journals/1367-2630/23/11/113004/revision2/njpac2c2aieqn10.gif) and
and ![${q}_{k}\enspace \mathrm{Tr}[{{\Pi}}_{k}]=\mathrm{Tr}[{\rho }_{{B}_{2}}{{\Pi}}_{k}]=p({m}_{2,k})$](https://content.cld.iop.org/journals/1367-2630/23/11/113004/revision2/njpac2c2aieqn11.gif) represent the initial probability that the observations of the magnetizations will yield m1,j
and m2,k
, respectively. The global density matrix can be expressed as
represent the initial probability that the observations of the magnetizations will yield m1,j
and m2,k
, respectively. The global density matrix can be expressed as
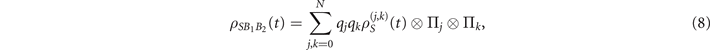
where each  represents the corresponding conditional reduced state of the system on the magnetic processing of the magnetizations m1,j
and m2,k
. Consequently, the full reduced state of the spin system at time t is
represents the corresponding conditional reduced state of the system on the magnetic processing of the magnetizations m1,j
and m2,k
. Consequently, the full reduced state of the spin system at time t is
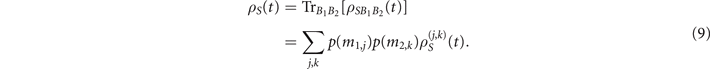
Owing to [HS , HI1 + HI2] = 0, the differential equation corresponding to the density matrix of the total system can be obtained by using the global von Neumann equation in the interaction picture:
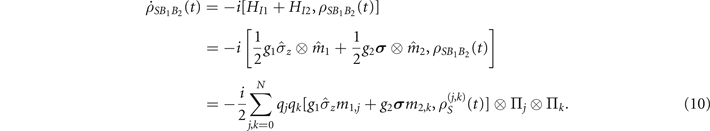
As no coupling occurs between different magnetization subspaces in our model, each of the conditional states  in equation (10) evolves independently. Therefore, we can obtain a set of uncoupled differential equations for each conditional state, as follows:
in equation (10) evolves independently. Therefore, we can obtain a set of uncoupled differential equations for each conditional state, as follows:
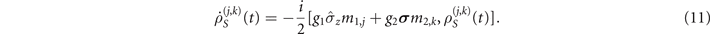
Subsequently, the above spin system dynamics can be rewritten in the Bloch sphere representation  , where the Bloch vector r unambiguously specifies the state of the system,
, where the Bloch vector r unambiguously specifies the state of the system,  , and
, and 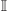 is the identity operator of the system. Therefore, equation (11) can be expressed as follows:
is the identity operator of the system. Therefore, equation (11) can be expressed as follows:
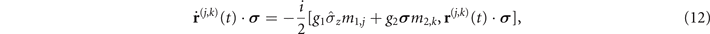
and

On the Cartesian basis, we drop the indices j, k and ignore the explicit time dependence for simplicity. Subsequently, equation (12) can be expanded into the following differential equations:
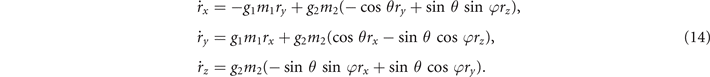
In the limit of N → ∞, the affine transformation can be performed in the following manner:
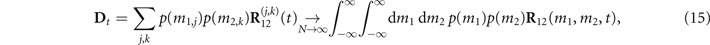
where R12(m1, m2, t), which possesses two magnetization parameters that are associated with each magnet, can be analytically acquired from equation (14). Hence, the Bloch vector r(t) of the density matrix at any time can be obtained from any initial state r(0).
2.2. Model B: induction of a static Zeeman field
By applying a static Zeeman field to drive a spin-1/2 system S, we mainly focus on the dynamics of the spin system coupled with a magnet B, as depicted in figure 1. Similar to model A, the magnetic environment follows a Gaussian distribution, and the free Hamiltonian of the magnet is selected as HB = 0. The Hamiltonian of the spin system that is affected by the static Zeeman field is as follows [62]:
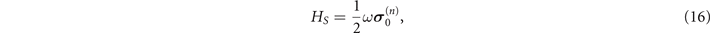
where ω behaves as the static Zeeman field and the component 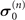 of the spin system can be selected as σx
, σy
, or σz
. The interaction Hamiltonian between the spin system and magnet is expressed as
of the spin system can be selected as σx
, σy
, or σz
. The interaction Hamiltonian between the spin system and magnet is expressed as
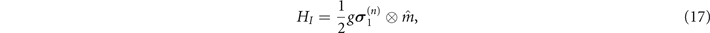
where the coupling strength between the system and magnet is g, and the coupling component of the spin system to the magnet is 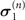 , which can also be selected as σx
, σy
, or σz
. Furthermore,
, which can also be selected as σx
, σy
, or σz
. Furthermore, 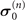 and
and  should be selected for a set of Pauli matrices that are not commutative with one another,
should be selected for a set of Pauli matrices that are not commutative with one another, ![$[{\boldsymbol{\sigma }}_{0}^{(n)},{\boldsymbol{\sigma }}_{1}^{(n)}]\ne 0$](https://content.cld.iop.org/journals/1367-2630/23/11/113004/revision2/njpac2c2aieqn21.gif) ; that is, corresponding to the case of [HS
, HI
] ≠ 0. Therefore, to solve the open system dynamics precisely by using the same calculation method as that of model A, we first need to compute the interaction Hamiltonian in the interaction picture:
; that is, corresponding to the case of [HS
, HI
] ≠ 0. Therefore, to solve the open system dynamics precisely by using the same calculation method as that of model A, we first need to compute the interaction Hamiltonian in the interaction picture:
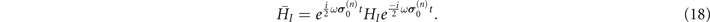
The initial state of the total system is considered as ρSB
(0) = ρS
(0) ⊗ ρB
, where the initial state of the magnetic environment is also selected as a classical mixture of different magnetizations 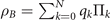 , in which qk
Tr[Πk
] = Tr[ρB
Πk
] = p(mk
) represents the initial probability that the observations of the magnetizations will yield mk
. Analogously to model A, using the global von Neumann equation, the Bloch vector
, in which qk
Tr[Πk
] = Tr[ρB
Πk
] = p(mk
) represents the initial probability that the observations of the magnetizations will yield mk
. Analogously to model A, using the global von Neumann equation, the Bloch vector 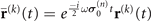 in the interaction picture represents the spin system state that is conditioned on the magnet possessing magnetization mk
:
in the interaction picture represents the spin system state that is conditioned on the magnet possessing magnetization mk
:
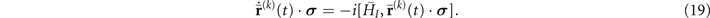
To obtain the solution of the differential equations, the homomorphism transformation of the SU2 group and SO3 group should be used by converting the unitary transformation element 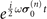 into
into 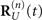 . In this case,
. In this case, 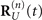 can be expressed in varying forms for the different
can be expressed in varying forms for the different 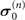 (n = x, y, or z):
(n = x, y, or z):
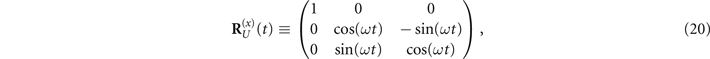
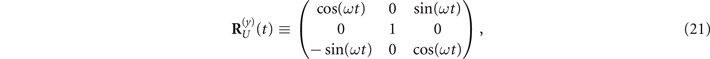
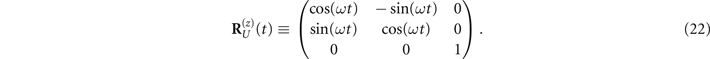
The differential equations proceed as follows:
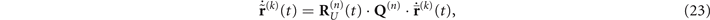
where Q(n) is also determined according to the different 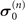 (n = x, y, or z):
(n = x, y, or z):
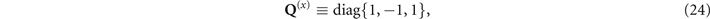
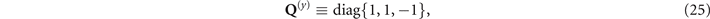
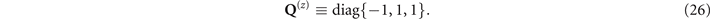
Following the above rotation operation Q(n), the matrix 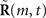 can be obtained, which contains the influence of the magnet. At this point, the differential equations of the above system become solvable. Subsequently, the solved matrix
can be obtained, which contains the influence of the magnet. At this point, the differential equations of the above system become solvable. Subsequently, the solved matrix  can be converted back into the interaction scenario:
can be converted back into the interaction scenario:
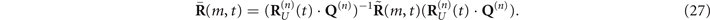
In the limit of N → ∞, we can obtain  for this model:
for this model:
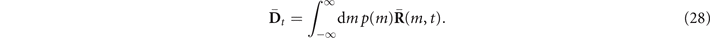
Thereafter, by substituting the result into  , the evolution-reduced density matrix of the spin system that is affected by a static Zeeman field can be obtained.
, the evolution-reduced density matrix of the spin system that is affected by a static Zeeman field can be obtained.
In the following, we set the initial state of the system to the maximal coherent state r(0) = (±1, 0, 0) for the above two models. Subsequently, we mainly analyze the control of the non-Markovian dynamics behavior of the spin system in the magnets under the above models.
3. Results and discussion: non-Markovian dynamics control
To describe the dynamics control from Markovianity to non-Markovianity by manipulating the spin system or magnet, we should first choose the appropriate measurement method of the memory effects of the dynamics of the open system. It is well known that quantum non-Markovianity is a multifaceted phenomenon and different methods for quantifying memory effects do not agree with each other in general [63–65]. However, for simple quantum systems such as the considered single spin-1/2 system the situation drastically simplifies and a measure of non-Markovianity (Breuer–Laine–Piilo method [11]) can be introduced. This method has been most widely used to measure non-Markovianity of the open two-level system, both experimentally and theoretically. Here, we also apply Breuer–Laine–Piilo method to measure the non-Markovianity of the process from the initial state ρ(0) to the final target state ρ(τ):
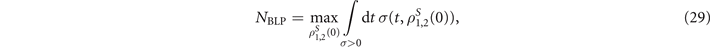
where ![$\sigma (t,{\rho }_{1,2}^{S}(0))=\mathrm{d}[D({\rho }_{1}^{S}(t),{\rho }_{2}^{S}(t))]/\mathrm{d}t$](https://content.cld.iop.org/journals/1367-2630/23/11/113004/revision2/njpac2c2aieqn33.gif) , and the trace distance
, and the trace distance 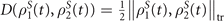 describes the distinguishability between two states, in which
describes the distinguishability between two states, in which 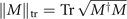 and 0 ⩽ D ⩽ 1. Moreover,
and 0 ⩽ D ⩽ 1. Moreover, 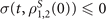 corresponds to all dynamical semigroups and all time-dependent Markovian processes. A non-Markovian evolution is defined as a process in which, for certain time intervals
corresponds to all dynamical semigroups and all time-dependent Markovian processes. A non-Markovian evolution is defined as a process in which, for certain time intervals 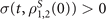 , the information flows back into the system temporarily, originating from the appearance of quantum memory effects. In references [11, 66], by drawing a sufficiently large sample of random pairs of initial states, it was proven that the optimal state pair of the initial states can be selected as
, the information flows back into the system temporarily, originating from the appearance of quantum memory effects. In references [11, 66], by drawing a sufficiently large sample of random pairs of initial states, it was proven that the optimal state pair of the initial states can be selected as 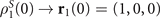 and
and 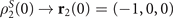 . Thus, in this section, we mainly apply this optimal initial state pair to calculate the non-Markovianity of the dynamics process that is affected by the magnetic environment. And the non-Markovian behaviors of the spin system in the following analyses are mainly obtained based on the Breuer–Laine–Piilo method of the non-Markovianity.
. Thus, in this section, we mainly apply this optimal initial state pair to calculate the non-Markovianity of the dynamics process that is affected by the magnetic environment. And the non-Markovian behaviors of the spin system in the following analyses are mainly obtained based on the Breuer–Laine–Piilo method of the non-Markovianity.
As noted in [31], the non-Markovian behavior in the dynamics process from the initial state ρ(0) to the final target state ρ(τ); that is, the associated information backflow from the reservoir to the system, can lead to faster quantum evolution, and hence, to a smaller QSLT. To analyze the connection between the non-Markovian behavior and quantum speedup process further, in the following, we illustrate the role of the second magnet or classical driving of the spin-1/2 system on the quantum speedup of the dynamics process. The QSLT can effectively define the bound of the minimal evolution time for arbitrary initial states and is helpful for analyzing the maximal evolution speed of a quantum open system. A much lower bound, as defined in [67], has been derived to describe the QSLT by relying on the Euclidean distance to measure the divisibility between two quantum states in the generalized Bloch sphere:

where 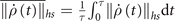 and
and 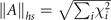 , χi
are the singular values of A. Furthermore, τ is set as the actual evolution time of the dynamics process from the initial state ρ(0) to the final target state ρ(τ). The advantage of this definition is that it is tighter and easier to compute in almost all quantum evolution processes. If τqsl/τ is equal to 1, the dynamics of the quantum state cannot be accelerated; that is, the evolutional speed has already reached its maximum. However, for τqsl/τ < 1, the dynamics of the quantum state may be accelerated. Moreover, a smaller value of τqsl/τ results in a greater quantum speedup.
, χi
are the singular values of A. Furthermore, τ is set as the actual evolution time of the dynamics process from the initial state ρ(0) to the final target state ρ(τ). The advantage of this definition is that it is tighter and easier to compute in almost all quantum evolution processes. If τqsl/τ is equal to 1, the dynamics of the quantum state cannot be accelerated; that is, the evolutional speed has already reached its maximum. However, for τqsl/τ < 1, the dynamics of the quantum state may be accelerated. Moreover, a smaller value of τqsl/τ results in a greater quantum speedup.
3.1. Model A: addition of a new magnet
Based on the original spin-magnet model, we add a new second magnet to affect the dynamics of the spin-1/2 system. The interaction Hamiltonians are provided by equations (4) and (5). By setting the initial state of the qubit to the maximal coherent states (the optimal state pair to calculate the non-Markovianity) rx = ±1, ry = rz = 0, we demonstrate how to manipulate the non-Markovianity of the open dynamics process under model A by adjusting two coupling direction angles (θ and φ) of the spin system to the new magnet, and the magnetic-related parameters (such as the standard deviations of the Gaussian distribution of two independent magnets).
First, for the spin system that is simultaneously coupled to two magnetic environments with the same components (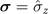 ; that is, [HI1, HI2] = 0), figure 2 indicates that the distinguishability between the two states described by the trace distance
; that is, [HI1, HI2] = 0), figure 2 indicates that the distinguishability between the two states described by the trace distance 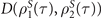 monotonically decreases with time by considering the different coupling strengths g2/g1 between the spin and two magnets. Thus, the non-Markvoianity of the dynamics process of the system is always zero, regardless of how the magnetic environments are controlled. This indicates that the Markovian dynamics of the system cannot be transformed into the non-Markovian process when the interaction Hamiltonians commute with one another. This result is the same as that of the system dynamics in the original spin-magnet model. The main reason for this is that, when [HI1, HI2] = 0, the system dynamics can be naively solved by adding the generators in equation (3).
monotonically decreases with time by considering the different coupling strengths g2/g1 between the spin and two magnets. Thus, the non-Markvoianity of the dynamics process of the system is always zero, regardless of how the magnetic environments are controlled. This indicates that the Markovian dynamics of the system cannot be transformed into the non-Markovian process when the interaction Hamiltonians commute with one another. This result is the same as that of the system dynamics in the original spin-magnet model. The main reason for this is that, when [HI1, HI2] = 0, the system dynamics can be naively solved by adding the generators in equation (3).
Figure 2. Trace distance 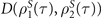 as function of actual evolution time τ with different coupling strengths g2/g1 between spin and two magnets in model A, with two initial states
as function of actual evolution time τ with different coupling strengths g2/g1 between spin and two magnets in model A, with two initial states 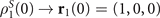 and
and  , in the case where the spin is simultaneously coupled to two magnets with the same components (
, in the case where the spin is simultaneously coupled to two magnets with the same components (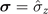 ), i.e. [HI1, HI2] = 0.
), i.e. [HI1, HI2] = 0.
Download figure:
Standard image High-resolution imageHence, for the purpose of obtaining the non-Markovian behavior of the dynamics process in model A, we investigate how to manipulate the non-Markovianity of the dynamics process in the case of the spin system that simultaneously interacts with two magnets by means of two different spin components ![$[{\hat{\sigma }}_{z},\boldsymbol{\sigma }]\ne 0$](https://content.cld.iop.org/journals/1367-2630/23/11/113004/revision2/njpac2c2aieqn48.gif) ; that is, the two interaction Hamiltonians do not commute with one another: [HI1, HI2] ≠ 0. Considering the two same magnets (λ1 = λ2), and the spin component
; that is, the two interaction Hamiltonians do not commute with one another: [HI1, HI2] ≠ 0. Considering the two same magnets (λ1 = λ2), and the spin component  of the second magnet, the non-Markovianity of the dynamics process from the initial state ρ(0) to the final target state ρ(τ) is presented in figure 3, where the parameters satisfy θ = π/2. We can explicitly determine that the original Markovian dynamics behavior (NBLP = 0) can be transformed into the new non-Markovian dynamics behavior (NBLP > 0) by introducing a second magnet that is coupled with the spin system, as indicated by the colored region in figure 3(b). This result is mainly because dynamics behavior corresponding to a system that simultaneously interacts with two magnets with two noncommutative interaction Hamiltonians cannot be constructed by the simple addition of the dynamics behavior associated with each individual environment. The cross-correlation that nay emerge between the two environments owing to their noncommutative interactions with the system leads to the new non-Markovian dynamics behavior.
of the second magnet, the non-Markovianity of the dynamics process from the initial state ρ(0) to the final target state ρ(τ) is presented in figure 3, where the parameters satisfy θ = π/2. We can explicitly determine that the original Markovian dynamics behavior (NBLP = 0) can be transformed into the new non-Markovian dynamics behavior (NBLP > 0) by introducing a second magnet that is coupled with the spin system, as indicated by the colored region in figure 3(b). This result is mainly because dynamics behavior corresponding to a system that simultaneously interacts with two magnets with two noncommutative interaction Hamiltonians cannot be constructed by the simple addition of the dynamics behavior associated with each individual environment. The cross-correlation that nay emerge between the two environments owing to their noncommutative interactions with the system leads to the new non-Markovian dynamics behavior.
Figure 3. Non-Markovianity of dynamics process from initial state ρ(0) to final target state ρ(τ) as function of actual evolution time τ in model A, with the system coupled to the same two magnets by the different spin components 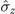 and
and 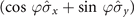 , which is satisfied by [HI1, HI2] ≠ 0. In this case, the parameters g1 = g2, λ1 = λ2.
, which is satisfied by [HI1, HI2] ≠ 0. In this case, the parameters g1 = g2, λ1 = λ2.
Download figure:
Standard image High-resolution imageAccording to figure 3, the effects of the direction angle φ (which implies the different spin components of the spin system of the second magnet) on the non-Markovianity of the open dynamics process can be investigated further. A remarkable behavior of the sudden transition from NBLP = 0 to NBLP > 0 is dependent on the selection of the final target state ρ(τ). There exists a critical evolution target state ρ(τc). In the case of the dynamics process with the actual evolution time τ < τc, the information backflow from the magnetic environments to the spin system never occurs, regardless of the selected value of φ. However, in the case of τ > τc, the information backflow always occurs based on the selection of an appropriate φ for coupling the component of the spin system to the second magnet. This means that the non-Markovian dynamics behavior of the dynamics process from ρ(0) to ρ(τ) (τ > τc) can be controlled by adding the second magnet that is coupled to the spin system.
Again, for a given dynamics process, such as the actual evolution dimensionless time τ = 4, it is worth noting that the non-Markovianity of the evolution will first gradually decrease and then gradually increase with an increase in φ in the region [0, π/2], as shown in figure 3(a). Moreover, when the interaction Hamiltonian between the spin system and added second magnetic environment satisfies 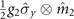 (corresponding to φ = π/2), the maximum non-Markovianity of the dynamics process can be acquired. Therefore, according to the above analysis, we obtain the interesting result that when the spin system is coupled to two independent magnets with two noncommutative interaction Hamiltonians, the new non-Markovian dynamics behavior of the spin can be achieved. Furthermore, in the case of a measurement of the component
(corresponding to φ = π/2), the maximum non-Markovianity of the dynamics process can be acquired. Therefore, according to the above analysis, we obtain the interesting result that when the spin system is coupled to two independent magnets with two noncommutative interaction Hamiltonians, the new non-Markovian dynamics behavior of the spin can be achieved. Furthermore, in the case of a measurement of the component 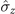 of the spin system by the first magnet, the maximum non-Markovianity of the dynamics process can be acquired by simultaneously measuring the component
of the spin system by the first magnet, the maximum non-Markovianity of the dynamics process can be acquired by simultaneously measuring the component 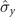 of the spin system by the second magnet, as illustrated in figure 3(a). However, when HI2 contains the two different spin components of the system (
of the spin system by the second magnet, as illustrated in figure 3(a). However, when HI2 contains the two different spin components of the system (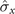 and
and 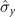 ) of the second magnet, it is clear that when the weights of the operators
) of the second magnet, it is clear that when the weights of the operators 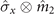 and
and 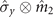 are closer (φ around π/4), the non-Markovianity of the dynamics process is reduced. A potential 'counteracting' effect exists in the production of the non-Markovian behavior of the dynamics process.
are closer (φ around π/4), the non-Markovianity of the dynamics process is reduced. A potential 'counteracting' effect exists in the production of the non-Markovian behavior of the dynamics process.
In the spin-magnet model, the standard deviation in the Gaussian distribution of the magnet and the coupling strength between the magnet and system are parameters that can be easily controlled. Thus, in the following, according to the case in which the spin system is coupled to two magnets with different components (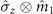 and
and 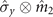 ), for the given coupling strength g1 between the spin system and first magnet with a standard deviation λ1 of the Gaussian distribution, we analyze the effects of the coupling strength of the system with the second magnet g2 and the standard deviation of the Gaussian distribution of this magnet λ2 on the non-Markovianity of the dynamics process, as illustrated in figure 4(a). We can explicitly conclude that the non-Markovianity first increases and then decreases with an increase in λ2. Furthermore, the maximum non-Markovianity of the dynamics process (ρ(0) to ρ(τ = 2)) is strongly dependent on the related parameters of the second magnet (g2 and λ2). The numerical calculation also demonstrates that the optimal value of the standard deviation of the Gaussian distribution of this magnet
), for the given coupling strength g1 between the spin system and first magnet with a standard deviation λ1 of the Gaussian distribution, we analyze the effects of the coupling strength of the system with the second magnet g2 and the standard deviation of the Gaussian distribution of this magnet λ2 on the non-Markovianity of the dynamics process, as illustrated in figure 4(a). We can explicitly conclude that the non-Markovianity first increases and then decreases with an increase in λ2. Furthermore, the maximum non-Markovianity of the dynamics process (ρ(0) to ρ(τ = 2)) is strongly dependent on the related parameters of the second magnet (g2 and λ2). The numerical calculation also demonstrates that the optimal value of the standard deviation of the Gaussian distribution of this magnet 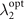 is determined by the coupling strength of the system to the second magnet g2. A smaller value of g2 results in a larger optimal value of
is determined by the coupling strength of the system to the second magnet g2. A smaller value of g2 results in a larger optimal value of 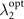 that should be requested. Taking the cases in figure 4(a) as examples, when g2 = 0.3g1, the optimal value of the standard deviation of the Gaussian distribution of this magnet is
that should be requested. Taking the cases in figure 4(a) as examples, when g2 = 0.3g1, the optimal value of the standard deviation of the Gaussian distribution of this magnet is 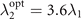 . In the cases of g2 = g1 and g2 = 3g1, we can obtain
. In the cases of g2 = g1 and g2 = 3g1, we can obtain 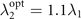 and
and 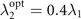 , respectively.
, respectively.
Figure 4. Non-Markovianity and QSLT of dynamics process from initial state ρ(0) to final target state ρ(τ) as function of standard deviation λ2 with different coupling strengths g2/g1, and dimensionless parameters τ = 2 and λ1 = 1. The spin system is coupled to two magnets with different components 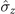 and
and  .
.
Download figure:
Standard image High-resolution imageIn recent years, it has been determined that the non-Markovianity of the dynamics process can be attributed to the quantum speedup of the evolution of a quantum system [31]. However, the question remains whether the one-to-one relationship between the non-Markovianity and quantum speedup holds true. Figure 4(b) describes the effects of the adjustable related parameters (g2 and λ2) of the second magnet on the QSLT of the spin system. It can clearly be observed that, as λ2 increases, the value of τqsl/τ can transition from τqsl/τ = 1 to τqsl/τ < 1, and then to τqsl/τ = 1. Similar to the analysis of the maximum non-Markovianity of the dynamics process (ρ(0) to ρ(τ = 2)), the optimal value of λ2 for the minimum τqsl/τ (which means the maximal quantum evolution speed) of this dynamics process is determined by the coupling strength of the system to the second magnet g2. As indicated in figure 4(b), a smaller value of g2 results in a larger optimal value of λ2 that should be requested. Thereafter, speedup evolution of the spin system can occur by selecting the suitable parameter region of λ2.
However, as opposed to the situation of previous studies, the QSLT is not strictly correlated with the occurrence of the non-Markovianity of the dynamics process, as illustrated in figure 4. Unexpectedly, non-Markovianity of the studied dynamics process exists, whereas the evolution speed of this dynamics process will not be accelerated, as indicated by the blue dotted lines in figures 4(a) and (b). Although the non-Markovianity may play an active role in the QSLT, the quantum speedup of the dynamics process is not only affected by the non-Markovianity. The geometric distance 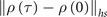 between the initial state ρ(0) and final target state ρ(τ) may also be an important factor affecting the QSLT.
between the initial state ρ(0) and final target state ρ(τ) may also be an important factor affecting the QSLT.
3.2. Model B: induction of a static Zeeman field
In the above subsection, it was explained that the non-Markovian dynamics behavior can be obtained by controlling the newly added magnet for the spin-1/2 system. At this point, we propose the other scheme for manipulating the non-Markovian dynamics behavior by applying a static Zeeman field on the spin-1/2 system. The spin system Hamiltonian HS
that is affected by the Zeeman field and the interaction Hamiltonian HI
are expressed as 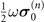 and
and 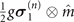 , respectively. By setting the initial state of the spin system to the maximal coherent state (the optimal state pair to calculate the non-Markovianity) rx
= ±1, ry
= rz
= 0, the dynamics of the system can be calculated using the method outlined in section 2.
, respectively. By setting the initial state of the spin system to the maximal coherent state (the optimal state pair to calculate the non-Markovianity) rx
= ±1, ry
= rz
= 0, the dynamics of the system can be calculated using the method outlined in section 2.
According to the different combinations of HS
and HI
in model B (labeled as (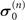 ,
, 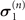 )), for a given dynamics process from the initial state ρ(0) to the final target state ρ(τ), the non-Markovianity and the QSLT for this dynamics process are calculated, as displayed in table 1. First, it can be clearly observed that the non-Markovian dynamics behavior and corresponding speedup dynamics of the evolution process never arise in the case of
)), for a given dynamics process from the initial state ρ(0) to the final target state ρ(τ), the non-Markovianity and the QSLT for this dynamics process are calculated, as displayed in table 1. First, it can be clearly observed that the non-Markovian dynamics behavior and corresponding speedup dynamics of the evolution process never arise in the case of 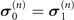 , which means that [HS
, HI
] = 0. However, according to table 1, in the case of the non-commutative relationship [HS
, HI
] ≠ 0, the non-Markovian dynamics behavior and corresponding speedup dynamics of the evolution process can be acquired in the remaining six combinations of HS
and HI
, namely (σx
, σy
), (σx
, σz
), (σy
, σx
), (σy
, σz
), (σz
, σx
), and (σz
, σy
). Interestingly, the same values of the non-Markovianity and QSLT for a given dynamics process can be obtained by the different combinations of the static Zeeman field of the spin component and the coupling of the spin component to the magnet (
, which means that [HS
, HI
] = 0. However, according to table 1, in the case of the non-commutative relationship [HS
, HI
] ≠ 0, the non-Markovian dynamics behavior and corresponding speedup dynamics of the evolution process can be acquired in the remaining six combinations of HS
and HI
, namely (σx
, σy
), (σx
, σz
), (σy
, σx
), (σy
, σz
), (σz
, σx
), and (σz
, σy
). Interestingly, the same values of the non-Markovianity and QSLT for a given dynamics process can be obtained by the different combinations of the static Zeeman field of the spin component and the coupling of the spin component to the magnet (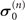 ,
, 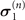 ); that is (i) (
); that is (i) (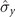 ,
, 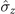 ) and (
) and (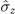 ,
, 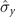 ), (ii) (
), (ii) (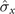 ,
,  ) and (
) and (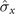 ,
, 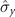 ), and (iii) (
), and (iii) (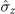 ,
, 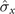 ) and (
) and (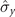 ,
, 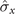 ).
).
Table 1. Non-Markovianity and QSLT under different combinations of HS and HI , with g = 1.
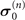
|
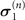
| τ | ω | λ | NBLP | τqsl/τ |
|---|---|---|---|---|---|---|
| σx | σx | 10 | 1 | 1 | 0 | 1 |
| 10 | 1 | 2 | 0 | 1 | ||
| 10 | 2 | 1 | 0 | 1 | ||
| σx | σy | 10 | 1 | 1 | 0.419 574 | 0.274 127 |
| 10 | 1 | 2 | 0.352 056 | 0.438 436 | ||
| 10 | 2 | 1 | 0.437 348 | 0.170 007 | ||
| σx | σz | 10 | 1 | 1 | 0.419 574 | 0.274 127 |
| 10 | 1 | 2 | 0.352 056 | 0.438 436 | ||
| 10 | 2 | 1 | 0.437 348 | 0.170 007 | ||
| σy | σx | 10 | 1 | 1 | 0.933 145 | 0.321 245 |
| 10 | 1 | 2 | 0.642 920 | 0.251 091 | ||
| 10 | 2 | 1 | 0.741 944 | 0.190 870 | ||
| σy | σy | 10 | 1 | 1 | 0 | 1 |
| 10 | 1 | 2 | 0 | 1 | ||
| 10 | 2 | 1 | 0 | 1 | ||
| σy | σz | 10 | 1 | 1 | 0.043 377 | 0.697 160 |
| 10 | 1 | 2 | 0.019 902 | 0.720 427 | ||
| 10 | 2 | 1 | 0.059 210 | 0.684 268 | ||
| σz | σx | 10 | 1 | 1 | 0.933 145 | 0.321 245 |
| 10 | 1 | 2 | 0.642 920 | 0.251 091 | ||
| 10 | 2 | 1 | 0.741 944 | 0.190 870 | ||
| σz | σy | 10 | 1 | 1 | 0.043 377 | 0.697 160 |
| 10 | 1 | 2 | 0.019 902 | 0.720 427 | ||
| 10 | 2 | 1 | 0.059 210 | 0.684 268 | ||
| σz | σz | 10 | 1 | 1 | 0 | 1 |
| 10 | 1 | 2 | 0 | 1 | ||
| 10 | 2 | 1 | 0 | 1 |
To investigate the effects of the different operation combinations in model B on the non-Markovianity of the dynamics process from ρ(0) to ρ(τ) further, figure 5 presents the phase diagram of the non-Markovianity under three different operation combinations (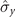 ,
,  ), (
), (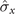 ,
, 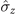 ), and (
), and (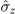 ,
, 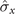 ). It can easily be observed that all these three operation combinations in model B can transform the original Markovian behavior into non-Markovian behavior when the appropriate parameters (ω and λ) are selected. The non-Markovianity is the weakest in case (i), whereas it is the strongest in case (iii). Thus, to acquire substantially greater non-Markovianity of the dynamics process, a static Zeeman field can be used along the
). It can easily be observed that all these three operation combinations in model B can transform the original Markovian behavior into non-Markovian behavior when the appropriate parameters (ω and λ) are selected. The non-Markovianity is the weakest in case (i), whereas it is the strongest in case (iii). Thus, to acquire substantially greater non-Markovianity of the dynamics process, a static Zeeman field can be used along the 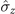 (or
(or  ) component of the spin system, which couples to the magnet in the
) component of the spin system, which couples to the magnet in the 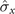 component.
component.
Figure 5. Phase diagram of non-Markovianity in three different operation combinations (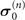 ,
, 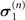 ): (a) and (d) for (
): (a) and (d) for ( ,
, 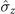 ), (b) and (e) for (
), (b) and (e) for (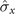 ,
, 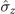 ), and (c) and (f) for (
), and (c) and (f) for (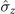 ,
, 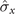 ). The parameters are set to ω/g = 1 in (a), (b), and (c) and λ/g = 1 in (d), (e), and (f).
). The parameters are set to ω/g = 1 in (a), (b), and (c) and λ/g = 1 in (d), (e), and (f).
Download figure:
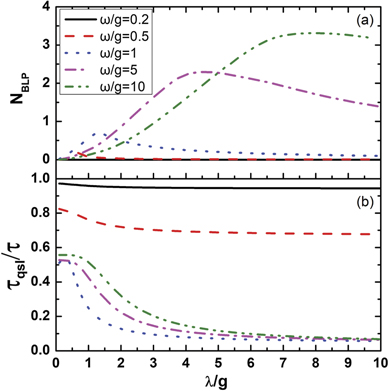
Standard image High-resolution imageMoreover, the static Zeeman field ω and standard deviation of the Gaussian distribution of the magnet λ are crucial to the appearance of non-Markovian behavior. Using the optimal operation combination (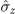 ,
, 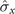 ) as an example, the non-Markovianity and QSLT of a given dynamics process from ρ(0) to ρ(τ = 6) are calculated as illustrated in figure 6. Therefore, by considering the different static Zeeman fields ω, we reach the interesting result that the non-Markovianity first increases and then decreases with an increase in the standard deviation λ of the magnet. Furthermore, there exists an optimal λopt that corresponds to the non-Markovianity maximum of the dynamics process. The optimal λopt and non-Markovianity maximum are strongly dependent on the static Zeeman field ω. A larger value of ω results in a larger optimal value of λopt that should be requested to acquire the larger non-Markovianity maximum, as illustrated in figure 6(a). Again, in the case of the weak static Zeeman field (such as the cases of ω/g = 0.2 and ω/g = 0.5 in figure 6(a)), it must be emphasized that the evolution of the spin system abides by the Markovian dynamics behavior and is hardly affected by the standard deviation of the Gaussian distribution of the magnet.
) as an example, the non-Markovianity and QSLT of a given dynamics process from ρ(0) to ρ(τ = 6) are calculated as illustrated in figure 6. Therefore, by considering the different static Zeeman fields ω, we reach the interesting result that the non-Markovianity first increases and then decreases with an increase in the standard deviation λ of the magnet. Furthermore, there exists an optimal λopt that corresponds to the non-Markovianity maximum of the dynamics process. The optimal λopt and non-Markovianity maximum are strongly dependent on the static Zeeman field ω. A larger value of ω results in a larger optimal value of λopt that should be requested to acquire the larger non-Markovianity maximum, as illustrated in figure 6(a). Again, in the case of the weak static Zeeman field (such as the cases of ω/g = 0.2 and ω/g = 0.5 in figure 6(a)), it must be emphasized that the evolution of the spin system abides by the Markovian dynamics behavior and is hardly affected by the standard deviation of the Gaussian distribution of the magnet.
Figure 6. Non-Markovianity and QSLT of dynamics process from initial state ρ(0) to final target state ρ(τ) as function of standard deviation λ when adding static Zeeman field to spin-1/2 system, with τ = 6, 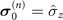 , and
, and  .
.
Download figure:
Standard image High-resolution imageMoreover, as indicated in figure 6(b), τqsl/τ is always less than 1, and it decreases with the increase in the standard deviation λ of the magnet, regardless of the value of ω. Therefore, in the model in which a static Zeeman field is applied on the spin system, the system evolution is always accelerated. Furthermore, according to figure 6(b), the intermediate value of the static Zeeman field ω has an impact on the smaller τqsl/τ, as indicated by the blue dotted line (ω/g = 1), whereas the non-Markovianity of this dynamics process is not larger. Compared to the previous analysis of the non-Markovianity, the stronger non-Markovianity does not lead to greater quantum acceleration. This again clearly demonstrates that there is no direct relationship between the non-Markovianity and quantum speedup of the dynamics process of the open system.
4. Conclusions
We have investigated the dynamics of the spin-1/2 system in two controllable spin-magnet models, in which two magnetic environments are coupled with the spin system (model A) or one magnetic environment interacts with a spin system that is affected by a static Zeeman field (model B). As the Gaussian distribution formally corresponds to the asymptotic limit of the magnet that is described by two microcanonical ensembles, we mainly considered the magnetization distribution for each magnet as a zero-mean Gaussian distribution in these two models. Several interesting phenomena were observed. Two dynamical crossovers of the quantum system were manipulated: from Markovian dynamics to non-Markovian dynamics and from no-speedup evolution to speedup evolution. For example, in model A, when the spin system was coupled to two independent magnets with two noncommutative interaction Hamiltonians [HI1, HI2] ≠ 0, the new non-Markovian dynamics and quantum speedup of the open system evolution could be achieved. Moreover, for the case of the coupled component 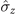 of the spin system with a magnet in the original spin-magnet model [61], the maximum non-Markovianity of the dynamics process could be acquired by simultaneously coupling the component
of the spin system with a magnet in the original spin-magnet model [61], the maximum non-Markovianity of the dynamics process could be acquired by simultaneously coupling the component 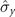 of the spin system using a new second magnet. In model B, the non-Markovian dynamics behavior and corresponding speedup dynamics of the evolution process could be obtained by applying a static Zeeman field on the spin system in the case where the system Hamiltonian HS
was affected by the Zeeman field and the interaction Hamiltonian HI
satisfied the noncommutative relationship [HS
, HI
] ≠ 0. Furthermore, substantially greater non-Markovianity of the dynamics process could be acquired by using a static Zeeman field along the component
of the spin system using a new second magnet. In model B, the non-Markovian dynamics behavior and corresponding speedup dynamics of the evolution process could be obtained by applying a static Zeeman field on the spin system in the case where the system Hamiltonian HS
was affected by the Zeeman field and the interaction Hamiltonian HI
satisfied the noncommutative relationship [HS
, HI
] ≠ 0. Furthermore, substantially greater non-Markovianity of the dynamics process could be acquired by using a static Zeeman field along the component 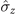 of the spin system, which was coupled to the magnet in the component
of the spin system, which was coupled to the magnet in the component 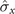 . Moreover, compared to the analysis of the non-Markovianity and QSLT in the considered spin-magnet models, the non-Markovianity was not the only reason for the quantum speedup. This result clearly illustrates the fact that no one-to-one relationship exists between the non-Markovianity and quantum speedup of the dynamics process of the spin system.
. Moreover, compared to the analysis of the non-Markovianity and QSLT in the considered spin-magnet models, the non-Markovianity was not the only reason for the quantum speedup. This result clearly illustrates the fact that no one-to-one relationship exists between the non-Markovianity and quantum speedup of the dynamics process of the spin system.
The spin-magnet model is a precisely solvable model of ferromagnetism [56, 57], which describes a measurement of the 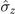 component of a spin-1/2 system by a magnet. It has recently been extended to measure several different components (
component of a spin-1/2 system by a magnet. It has recently been extended to measure several different components (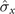 ,
, 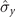 and
and 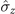 ) of the spin-1/2 system simultaneously [58]. Thus, the simultaneous coupling of the different components of the spin system by the magnets in our considered models is theoretically reliable. Furthermore, both models could also be realized experimentally in various actual physical systems. In 2016, the authors obtained simultaneously measured noncommuting observables in experiments [68]. They implemented two high-quantum-efficiency readouts of the angular momenta about two different axes of an artificial spin-1/2 system, and observed the resulting dynamics in real time. Therefore, as the spin-1/2 system interacts with the environment via noncommuting degrees of freedom in our model A, reference [68] offers a means of studying the quantum dynamics of simultaneously measured noncommuting observables of the spin-1/2 system. Our proposed model A also has a practical connection with possible experimental scenarios.
) of the spin-1/2 system simultaneously [58]. Thus, the simultaneous coupling of the different components of the spin system by the magnets in our considered models is theoretically reliable. Furthermore, both models could also be realized experimentally in various actual physical systems. In 2016, the authors obtained simultaneously measured noncommuting observables in experiments [68]. They implemented two high-quantum-efficiency readouts of the angular momenta about two different axes of an artificial spin-1/2 system, and observed the resulting dynamics in real time. Therefore, as the spin-1/2 system interacts with the environment via noncommuting degrees of freedom in our model A, reference [68] offers a means of studying the quantum dynamics of simultaneously measured noncommuting observables of the spin-1/2 system. Our proposed model A also has a practical connection with possible experimental scenarios.
Moreover, one coherent driving Hamiltonian that corresponds to a simple quantum rotation operation on the qubit can easily be implemented in experiments. The additional driving field (static Zeeman field) acting on the spin-1/2 system is a key part of model B. Two non-interacting spin-1/2 particles that interact with a magnet and a Zeeman field that acts exclusively on the first spin have been investigated [62]. The Zeeman field in [62] that contains two parts (a static Zeeman field and a time-varying Zeeman field) was used to affect the spin system. These authors experimentally demonstrated their method on an ensemble of optically trapped 87Rb atoms. In our model B, we mainly considered a spin-1/2 particle that interacted with a magnet and a static Zeeman field that acted exclusively on the spin. Thus, the experimental implementation of our model B was inspired by reference [62]. Furthermore, a strongly driven two-level system with a driving frequency that is four times larger than its precession frequency was realized using radiation-dressed states of nitrogen-vacancy centers in diamond [69]. The schemes were experimentally realized with the driving Hamiltonian in a superconducting transmon system [70] and in a superconducting quantum circuit [71].
Therefore, according to these potential candidates for the spin-magnet model and the coherent driving mechanisms, our two proposed non-Markovian dynamics control schemes are experimentally feasible. Such non-Markovian speedup dynamics control based on the spin-magnet model is essential for most purposes of quantum optimal control.
Acknowledgments
This work is supported by the Provincial Natural Science Foundation of Shandong (ZR2020MA086), the National Natural Science Foundation of China (61675115, 11974209), MOST of China (2016YFA0302104, 2016YFA0300600), Taishan Scholar Project of Shandong Province (China) (TSQN201812059).
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).