Article contents
 $H$-theorem and boundary conditions for the linear R26 equations: application to flow past an evaporating droplet
$H$-theorem and boundary conditions for the linear R26 equations: application to flow past an evaporating droplet
Published online by Cambridge University Press: 05 August 2021
Abstract
Determining physically admissible boundary conditions for higher moments in an extended continuum model is recognised as a major obstacle. Boundary conditions for the regularised 26-moment (R26) equations obtained using Maxwell's accommodation model do exist in the literature; however, we show in this article that these boundary conditions violate the second law of thermodynamics and the Onsager reciprocity relations for certain boundary value problems, and, hence, are not physically admissible. We further prove that the linearised R26 (LR26) equations possess a proper  $H$-theorem (second-law inequality) by determining a quadratic form without cross-product terms for the entropy density. The establishment of the
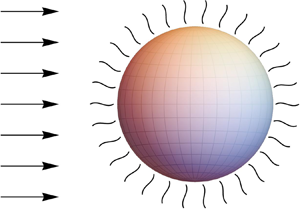
$H$-theorem (second-law inequality) by determining a quadratic form without cross-product terms for the entropy density. The establishment of the  $H$-theorem for the LR26 equations in turn leads to a complete set of boundary conditions that are physically admissible for all processes and comply with the Onsager reciprocity relations. As an application, the problem of a slow rarefied gas flow past a spherical droplet with and without evaporation is considered and solved analytically. The results are compared with the numerical solution of the linearised Boltzmann equation, experimental results from the literature and/or other macroscopic theories to show that the LR26 theory with the physically admissible boundary conditions provides an excellent prediction up to Knudsen number
$H$-theorem for the LR26 equations in turn leads to a complete set of boundary conditions that are physically admissible for all processes and comply with the Onsager reciprocity relations. As an application, the problem of a slow rarefied gas flow past a spherical droplet with and without evaporation is considered and solved analytically. The results are compared with the numerical solution of the linearised Boltzmann equation, experimental results from the literature and/or other macroscopic theories to show that the LR26 theory with the physically admissible boundary conditions provides an excellent prediction up to Knudsen number  $\lesssim 1$ and, consequently, provides transpicuous insights into intriguing effects, such as thermal polarisation. In particular, the analytic results for the drag force obtained in the present work are in an excellent agreement with experimental results even for very large values of the Knudsen number.
$\lesssim 1$ and, consequently, provides transpicuous insights into intriguing effects, such as thermal polarisation. In particular, the analytic results for the drag force obtained in the present work are in an excellent agreement with experimental results even for very large values of the Knudsen number.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 6
- Cited by




