Skip to main content
SpringerLink
Log in

A receding contact problem between a graded piezoelectric layer and a piezoelectric substrate

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

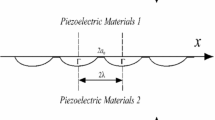
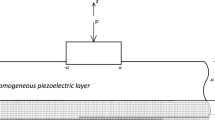
The receding contact problem between a graded piezoelectric layer and a homogeneous piezoelectric substrate is considered in this paper. It is assumed that the gradation of the elastic piezoelectric graded layer is of exponential type through its thickness. Using standard Fourier transform, the contact problem is converted to a system of two singular integral equations in which the contact pressures and the electric charge displacement in addition to the contact dimensions are the unknowns. The integral equations are then solved numerically using Gauss–Jacobi integration formula. The primary objective of this paper is to investigate the effect of material gradation on the contact pressure, electric charge distribution and on the length of the receding contact. The main findings of the paper are that the inhomogeneity parameter has a strong effect on the contact pressure and the electric charge distribution at the receding contact interface. It is concluded that a softer FGPM in \(+z\) direction results in lower contact pressure and electric displacement.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Yilmaz, K.B., Comez, I., Yildirim, B., Güler, M.A., El-Borgi, S.: Frictional receding contact problem for a graded bilayer system indented by a rigid punch. International Journal of Mechanical Sciences 141, 127–142 (2018)

    Article  Google Scholar 

  2. El-Borgi, S., Abdelmoula, R., Keer, L.: A receding contact plane problem between a functionally graded layer and a homogeneous substrate. International Journal of Solids and Structures 43(3–4), 658–674 (2006)

    Article  Google Scholar 

  3. Rhimi, M., El-Borgi, S., Ben Said, W., Ben Jemaa, F.: A receding contact axisymmetric problem between a functionally graded layer and a homogeneous substrate. International Journal of Solids and Structures 46(20), 3633–3642 (2009)

    Article  Google Scholar 

  4. Rhimi, M., El-Borgi, S., Lajnef, N.: A double receding contact axisymmetric problem between a functionally graded layer and a homogeneous substrate. Mechanics of Materials 43(12), 787–798 (2011)

    Article  Google Scholar 

  5. El-Borgi, S., Usman, S., Güler, M.A.: A frictional receding contact plane problem between a functionally graded layer and a homogeneous substrate. International Journal of Solids and Structures 51(25–26), 4462–4476 (2014)

    Article  Google Scholar 

  6. Yan, J., Li, X.: Double receding contact plane problem between a functionally graded layer and an elastic layer. European Journal of Mechanics-A/Solids 53, 143–150 (2015)

    Article  MathSciNet  Google Scholar 

  7. Yan, J., Mi, C.: On the receding contact between an inhomogeneously coated elastic layer and a homogeneous half-plane. Mechanics of Materials 112, 18–27 (2017)

    Article  Google Scholar 

  8. El-Borgi, S., Çömez, I.: A receding frictional contact problem between a graded layer and a homogeneous substrate pressed by a rigid punch. Mechanics of Materials 114, 201–214 (2017)

    Article  Google Scholar 

  9. Lopes, J.P., Hills, D.A.: The axisymmetric frictional receding contact of a layer pressed against a half-space by pressure outside a disk. European Journal of Mechanics-A/Solids 77, 103787 (2019)

    Article  MathSciNet  Google Scholar 

  10. KS Parel. Plane frictional receding contact of a thin layer pressed onto a substrate by finite pressure distributions. European Journal of Mechanics-A/Solids, page 104309, 2021

  11. Cao, R., Li, L., Li, X., Mi, C.: On the frictional receding contact between a graded layer and an orthotropic substrate indented by a rigid flat-ended stamp. Mechanics of Materials 158, 103847 (2021)

    Article  Google Scholar 

  12. Tian, X.J., Zhou, Y.T., Guan, X.F., Wang, L.H., Ding, S.H.: The frictional contact problem of a rigid punch sliding over thermoelectric materials. International Journal of Solids and Structures 200, 145–157 (2020)

    Article  Google Scholar 

  13. Li, X., Tian, X.J., Zhou, Y.T.: Thickness size effect on contact behavior of a thermoelectric strip. Acta Mechanica , 1–17 (2021)

  14. Liu, J., Ke, L.-L., Zhang, C.: Axisymmetric thermoelastic contact of an fgm-coated half-space under a rotating punch. Acta Mechanica , 1–18 (2021)

  15. Zhou, Y.T., Tian, X.J., Li, F.J.: On coupling contact analysis of thermoelectric materials. Applied Mathematical Modelling 89, 1459–1474 (2021)

    Article  MathSciNet  Google Scholar 

  16. Ke, L.-L., Yang, J., Kitipornchai, S., Wang, Y.-S.: Electro-mechanical frictionless contact behavior of a functionally graded piezoelectric layered half-plane under a rigid punch. International Journal of Solids and Structures 45(11–12), 3313–3333 (2008)

    Article  Google Scholar 

  17. Ke, L.-L., Yang, J., Kitipornchai, S., Wang, Y.-S.: Frictionless contact analysis of a functionally graded piezoelectric layered half-plane. Smart Materials and Structures 17(2), 025003 (2008)

  18. Su, J., Ke, L.-L., Wang, Y.-S.: Fretting contact of a functionally graded piezoelectric layered half-plane under a conducting punch. Smart Materials and Structures 25(2), 025014 (2016)

  19. Liu, T.-J., Zhang, C.: Axisymmetric conducting indenter on a functionally graded piezoelectric coating. International Journal of Mechanical Sciences 115, 34–44 (2016)

    Article  Google Scholar 

  20. Liu, T.-J., Li, P., Zhang, C.: On contact problem with finite friction for a graded piezoelectric coating under an insulating spherical indenter. International Journal of Engineering Science 121, 1–13 (2017)

    Article  MathSciNet  Google Scholar 

  21. Su, J., Ke, L.-L., El-Borgi, S., Xiang, Y., Wang, Y.-S.: An effective method for the sliding frictional contact of a conducting cylindrical punch on fgpms. International Journal of Solids and Structures 141, 127–136 (2018)

    Article  Google Scholar 

  22. Zhou, Y.-T., Zhang, C., Zhong, Z., Wang, L.: Transient thermo-electro-elastic contact analysis of a sliding punch acting on a functionally graded piezoelectric strip under non-fourier heat conduction. European Journal of Mechanics-A/Solids 73, 90–100 (2019)

    Article  MathSciNet  Google Scholar 

  23. Tian, X.J., Zhou, Y.T., Wang, L.H., Ding, S.H.: Surface contact behavior of functionally graded thermoelectric materials indented by a conducting punch. Applied Mathematics 42(5), 649–664 (2021)

    MathSciNet  Google Scholar 

  24. Giannakopoulos, A.E., Suresh, S.: Theory of indentation of piezoelectric materials. Acta materialia 47(7), 2153–2164 (1999)

    Article  Google Scholar 

  25. Erdogan, F., Gupta, G.D.: On the numerical solution of singular integral equations. Quarterly of Applied Mathematics 29, 525–534 (1972)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The first author is grateful for the funding provided by Texas A&M University at Qatar. The authors are also grateful for the help of Mrs. Hedia Layouni El-Borgi in typesetting the Latex document.

Author information

Authors and Affiliations

  1. Mechanical Engineering Program, Texas A&M University at Qatar, Engineering Building, P.O. Box 23874, Education City, Doha, Qatar

    Sami El-Borgi

  2. Department of Civil Engineering, Karadeniz Technical University, 61080, Ortahisar-Trabzon, Turkey

    Isa Çömez

  3. College of Engineering and Technology, American University of the Middle East, Egaila, Kuwait

    Mehmet Ali Güler

Authors
  1. Sami El-Borgi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Isa Çömez
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mehmet Ali Güler
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sami El-Borgi.

Ethics declarations

Conflict of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix A

Appendix A

1.1 Expressions of quantities appearing in Eq. (17)

$$\begin{aligned} \alpha _6&= -c_{{330}}c_{{440}}\epsilon _{{330}}-c_{{440}}e_{330}^{2} \end{aligned}$$
(A.1a)
$$\begin{aligned} \alpha _5&= -3\,\beta \,c_{{330}}c_{{440}}\epsilon _{{330}}-3\,\beta \,c_{{440}}e_{{330}}^{2} \end{aligned}$$
(A.1b)
$$\begin{aligned} \alpha _4&=-3\,{\beta }^{2}c_{{330}}c_{{440}}\epsilon _{{330}}-3\,{\beta }^{2}c_{{ 440}}{e_{{330}}}^{2}+{\lambda }^{2}c_{{110}}c_{{330}}\epsilon _{{330}}+{ \lambda }^{2}c_{{110}}{e_{{330}}}^{2}\nonumber \\&-{\lambda }^{2}{c_{{130}}}^{2} \epsilon _{{330}}-2\,{\lambda }^{2}c_{{130}}c_{{440}}\epsilon _{{330}}-2 \,{\lambda }^{2}c_{{130}}e_{{150}}e_{{330}}-2\,{\lambda }^{2}c_{{130}}e_ {{310}}e_{{330}}+\nonumber \\&{\lambda }^{2}c_{{330}}c_{{440}}\epsilon _{{110}}+{ \lambda }^{2}c_{{330}}{e_{{150}}}^{2}+2\,{\lambda }^{2}c_{{330}}e_{{150} }e_{{310}}+{\lambda }^{2}c_{{330}}{e_{{310}}}^{2}-2\,{\lambda }^{2}c_{{ 440}}e_{{310}}e_{{330}} \end{aligned}$$
(A.1c)
$$\begin{aligned} \alpha _3&= -{\beta }^{3}c_{{330}}c_{{440}}\epsilon _{{330}}-{\beta }^{3}c_{{440}}{e_ {{330}}}^{2}+2\,\beta \,{\lambda }^{2}c_{{110}}c_{{330}}\epsilon _{{330}} +2\,\beta \,{\lambda }^{2}c_{{110}}{e_{{330}}}^{2}-\nonumber \\&2\,\beta \,{\lambda }^{ 2}{c_{{130}}}^{2}\epsilon _{{330}}-4\,\beta \,{\lambda }^{2}c_{{130}}c_{{ 440}}\epsilon _{{330}}-4\,\beta \,{\lambda }^{2}c_{{130}}e_{{150}}e_{{330 }}-4\,\beta \,{\lambda }^{2}c_{{130}}e_{{310}}e_{{330}}+\nonumber \\ {}&2\,\beta \,{ \lambda }^{2}c_{{330}}c_{{440}}\epsilon _{{110}}+2\,\beta \,{\lambda }^{2} c_{{330}}{e_{{150}}}^{2}+4\,\beta \,{\lambda }^{2}c_{{330}}e_{{150}}e_{{ 310}}+2\,\beta \,{\lambda }^{2}c_{{330}}{e_{{310}}}^{2}-\nonumber \\ {}&4\,\beta \,{ \lambda }^{2}c_{{440}}e_{{310}}e_{{330}} \end{aligned}$$
(A.1d)
$$\begin{aligned} \alpha _2&= {\beta }^{2}{\lambda }^{2}c_{{110}}c_{{330}}\epsilon _{{330}}+{\beta }^{2} {\lambda }^{2}c_{{110}}{e_{{330}}}^{2}-{\beta }^{2}{\lambda }^{2}{c_{{130 }}}^{2}\epsilon _{{330}}-3\,{\beta }^{2}{\lambda }^{2}c_{{130}}c_{{440}} \epsilon _{{330}}-\nonumber \\ {}&3\,{\beta }^{2}{\lambda }^{2}c_{{130}}e_{{150}}e_{{330} }-2\,{\beta }^{2}{\lambda }^{2}c_{{130}}e_{{310}}e_{{330}}+{\beta }^{2}{ \lambda }^{2}c_{{330}}c_{{440}}\epsilon _{{110}}+{\beta }^{2}{\lambda }^{2 }c_{{330}}{e_{{150}}}^{2}+\nonumber \\ {}&3\,{\beta }^{2}{\lambda }^{2}c_{{330}}e_{{150} }e_{{310}}+{\beta }^{2}{\lambda }^{2}c_{{330}}{e_{{310}}}^{2}-3\,{\beta } ^{2}{\lambda }^{2}c_{{440}}e_{{310}}e_{{330}}-{\lambda }^{4}c_{{110}}c_{ {330}}\epsilon _{{110}}-\nonumber \\ {}&{\lambda }^{4}c_{{110}}c_{{440}}\epsilon _{{330}} -2\,{\lambda }^{4}c_{{110}}e_{{150}}e_{{330}}+{\lambda }^{4}{c_{{130}}}^ {2}\epsilon _{{110}}+2\,{\lambda }^{4}c_{{130}}c_{{440}}\epsilon _{{110}} +2\,{\lambda }^{4}c_{{130}}{e_{{150}}}^{2}+\nonumber \\ {}&2\,{\lambda }^{4}c_{{130}}e_{ {150}}e_{{310}}-{\lambda }^{4}c_{{440}}{e_{{310}}}^{2} \end{aligned}$$
(A.1e)
$$\begin{aligned} \alpha _1&= -{\beta }^{3}{\lambda }^{2}c_{{130}}c_{{440}}\epsilon _{{330}}-{\beta }^{3 }{\lambda }^{2}c_{{130}}e_{{150}}e_{{330}}+{\beta }^{3}{\lambda }^{2}c_{{ 330}}e_{{150}}e_{{310}}-{\beta }^{3}{\lambda }^{2}c_{{440}}e_{{310}}e_{{ 330}}-\nonumber \\ {}&\beta \,{\lambda }^{4}c_{{110}}c_{{330}}\epsilon _{{110}}-\beta \,{ \lambda }^{4}c_{{110}}c_{{440}}\epsilon _{{330}}-2\,\beta \,{\lambda }^{4} c_{{110}}e_{{150}}e_{{330}}+\beta \,{\lambda }^{4}{c_{{130}}}^{2} \epsilon _{{110}}+\nonumber \\ {}&2\,\beta \,{\lambda }^{4}c_{{130}}c_{{440}}\epsilon _{{ 110}}+2\,\beta \,{\lambda }^{4}c_{{130}}{e_{{150}}}^{2}+2\,\beta \,{ \lambda }^{4}c_{{130}}e_{{150}}e_{{310}}-\beta \,{\lambda }^{4}c_{{440}}{ e_{{310}}}^{2} \end{aligned}$$
(A.1f)
$$\begin{aligned} \alpha _0&= {\lambda }^{4} \left( c_{{440}}\epsilon _{{110}}+{e_{{150}}}^{2} \right) \left( {\beta }^{2}c_{{130}}+{\lambda }^{2}c_{{110}} \right) \end{aligned}$$
(A.1g)

1.2 Expressions of quantities appearing in Eq. (24)

$$\begin{aligned} \gamma _6&= -c_{{330}}c_{{440}}\epsilon _{{330}}-c_{{440}}e_{330}^{2} \end{aligned}$$
(A.2a)
$$\begin{aligned} \gamma _4&= {\lambda }^{2}c_{{110}}c_{{330}}\epsilon _{{330}}+{\lambda }^{2}c_{{110}} {e_{{330}}}^{2}-{\lambda }^{2}{c_{{130}}}^{2}\epsilon _{{330}}-2\,{ \lambda }^{2}c_{{130}}c_{{440}}\epsilon _{{330}}-\nonumber \\ {}&2\,{\lambda }^{2}c_{{130 }}e_{{150}}e_{{330}}- 2\,{\lambda }^{2}c_{{130}}e_{{310}}e_{{330}}+{ \lambda }^{2}c_{{330}}c_{{440}}\epsilon _{{110}}+{\lambda }^{2}c_{{330}}{ e_{{150}}}^{2}+\nonumber \\ {}&2\,{\lambda }^{2}c_{{330}}e_{{150}}e_{{310}}+{\lambda }^{ 2}c_{{330}}{e_{{310}}}^{2}- 2\,{\lambda }^{2}c_{{440}}e_{{310}}e_{{330}} \end{aligned}$$
(A.2b)
$$\begin{aligned} \gamma _2&= -{\lambda }^{4}c_{{110}}c_{{330}}\epsilon _{{110}}-{\lambda }^{4}c_{{110} }c_{{440}}\epsilon _{{330}}-2\,{\lambda }^{4}c_{{110}}e_{{150}}e_{{330}} +{\lambda }^{4}{c_{{130}}}^{2}\epsilon _{{110}}+\nonumber \\ {}&2\,{\lambda }^{4}c_{{130} }c_{{440}}\epsilon _{{110}}+ 2\,{\lambda }^{4}c_{{130}}{e_{{150}}}^{2}+2 \,{\lambda }^{4}c_{{130}}e_{{150}}e_{{310}}-{\lambda }^{4}c_{{440}}{e_{{ 310}}}^{2} \end{aligned}$$
(A.2c)
$$\begin{aligned} \gamma _0&= {\lambda }^{6}c_{{110}} \left( c_{{440}}\epsilon _{{110}}+e_{{150}}^{2 } \right) \end{aligned}$$
(A.2d)

1.3 Expressions of quantities appearing in Eqs. (33) and (34)

$$\begin{aligned}&A(\lambda ,z) = 2\lambda \left( \sum \limits _{k = 1}^6 (- 1)^k{S_k}\frac{{{D_{4k}}}}{D}{\mathrm{e}^{{m_k}z}} + \sum \limits _{k = 1}^3 ( - 1)^k{S_{2k+5}}\frac{{{{\bar{D}}_{1k}}}}{{\bar{D}}}{\mathrm{e}^{{n_k}z}}\right) \end{aligned}$$
(A.3a)
$$\begin{aligned}&G(\lambda ,z) = 2\lambda \left( \sum \limits _{k = 1}^6 (-1)^k{S_k}\frac{{{D_{6k}}}}{D}{\mathrm{e}^{{m_k}z}} + \sum \limits _{k = 1}^3 (-1)^k{S_{2k+5}}\frac{{{{\bar{D}}_{3k}}}}{{\bar{D}}}{\mathrm{e}^{{n_k}z}}\right) \end{aligned}$$
(A.3b)
$$\begin{aligned}&F_{11}(x,t) = \int _{ 0 }^{ + \infty } 2 \lambda \mathrm{e}^{-\beta h} \left( \sum \limits _{k = 1}^6(- 1)^k {S_k}\frac{{{D_{1k}}}}{D}\right) \sin \left( \lambda (t-x)\right) \mathrm{d}\lambda \end{aligned}$$
(A.3c)
$$\begin{aligned}&F_{12}(x,t) = \int _{ 0 }^{ + \infty } 2 \lambda \mathrm{e}^{-\beta h} \left( \sum \limits _{k = 1}^6(- 1)^k {S_k}\frac{{{D_{3k}}}}{D}\right) \sin \left( \lambda (t-x)\right) \mathrm{d}\lambda \end{aligned}$$
(A.3d)

1.4 Expressions of quantities appearing in Eqs. (35) and (36)

$$\begin{aligned}&B(\lambda ,z) = 2\lambda \left( \sum \limits _{k = 1}^6 (- 1)^k{N_k}\frac{{{D_{4k}}}}{D} + \sum \limits _{k = 1}^3 ( - 1)^k{N_{2k+5}}\frac{{{{\bar{D}}_{1k}}}}{{\bar{D}}}\right) \end{aligned}$$
(A.4a)
$$\begin{aligned}&H(\lambda ,z) = 2\lambda \left( \sum \limits _{k = 1}^6 (-1)^k{N_k}\frac{{{D_{6k}}}}{D} + \sum \limits _{k = 1}^3 (-1)^k{N_{2k+5}}\frac{{{{\bar{D}}_{3k}}}}{{\bar{D}}}\right) \end{aligned}$$
(A.4b)
$$\begin{aligned}&F_{21}(x,t) = \int _{ 0 }^{ + \infty } 2 \lambda \mathrm{e}^{-\beta h} \left( \sum \limits _{k = 1}^6(- 1)^k {N_k}\frac{{{D_{1k}}}}{D}\right) \sin \left( \lambda (t-x)\right) \mathrm{d}\lambda \end{aligned}$$
(A.4c)
$$\begin{aligned}&F_{22}(x,t) = \int _{ 0 }^{ + \infty } 2 \lambda \mathrm{e}^{-\beta h} \left( \sum \limits _{k = 1}^6(- 1)^k {N_k}\frac{{{D_{3k}}}}{D}\right) \sin \left( \lambda (t-x)\right) \mathrm{d}\lambda \end{aligned}$$
(A.4d)

1.5 Expressions of quantities appearing in Eq. (39)

$$\begin{aligned}&{\bar{K}}_{11}(x,t) = \int _{ 0 }^{ + \infty } \left[ A(\lambda ,0) - a_0\right] \sin \left( \lambda (t-x)\right) \mathrm{d}\lambda \end{aligned}$$
(A.5a)
$$\begin{aligned}&{\bar{K}}_{12}(x,t) = \int _{ 0 }^{ + \infty } \left[ G(\lambda ,0) - g_0\right] \sin \left( \lambda (t-x)\right) \mathrm{d}\lambda \end{aligned}$$
(A.5b)
$$\begin{aligned}&{\bar{K}}_{21}(x,t) = \int _{ 0 }^{ + \infty } \left[ B(\lambda ,0) - b_0\right] \sin \left( \lambda (t-x)\right) \mathrm{d}\lambda \end{aligned}$$
(A.5c)
$$\begin{aligned}&{\bar{K}}_{22}(x,t) = \int _{ 0 }^{ + \infty } \left[ H(\lambda ,0) - h_0\right] \sin \left( \lambda (t-x)\right) \mathrm{d}\lambda \end{aligned}$$
(A.5d)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

El-Borgi, S., Çömez, I. & Ali Güler, M. A receding contact problem between a graded piezoelectric layer and a piezoelectric substrate. Arch Appl Mech 91, 4835–4854 (2021). https://doi.org/10.1007/s00419-021-02037-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-021-02037-6

Keywords

Search

Navigation