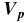ELECTROMAGNETIC WAVES NEAR THE PROTON CYCLOTRON FREQUENCY: STEREO OBSERVATIONS

Electromagnetic waves near the proton cyclotron frequency (f_pc) can be left-hand (LH) polarized ion cyclotron waves (ICWs) or right-hand (RH) polarized magnetosonic waves (e.g., p. 106 of Gary 1993). They appear to be circularly (when parallel-propagating) or elliptically (when obliquely propagating, e.g., Stix 1962; Cowee et al. 2007; Omidi et al. 2011) polarized transverse waves. We call them low-frequency waves (LFWs) in this study. Because ICWs and Alfvén waves (e.g., Belcher et al. 1969; Belcher & Davis 1971) share the same LH branch in the wave dispersion diagram, the LH polarized waves are also called Alfvén/ion cyclotron waves (e.g., p. 107 of Gary 1993). Both ICWs and Alfvén waves are associated with magnetic perturbation transverse to the background magnetic field. The ICWs are at or slightly below f_pc and are often treated in a hybrid simulation, whereas Alfvén waves are at a lower frequency range and can be treated in the magnetohydrodynamic approximation. The RH branch is shared by magnetosonic waves and electron cyclotron (whistler) waves. In the frequency range near f_pc, the waves are described as magnetosonic/whistler waves (e.g., p. 110 of Gary 1993). They become whistler waves at higher frequency (near the electron cyclotron frequency f_ec) and compressive magnetosonic waves at lower frequency where the fluctuations of magnetic field and proton density are correlated. For obliquely propagating LFWs, the mode conversion, i.e., the change of the dominant sense of polarization, can happen near the crossover frequency where the LH and RH polarized waves have the same phase speed (e.g., Smith & Brice 1964; Budden 1985). For parallel-propagating LFWs, the LH and RH polarizations are decoupled, and the waves do not exchange polarization.

Waves near f_pc are important because the absorption of fluctuating magnetic field energy starting at f_pc in turbulent cascades has been demonstrated extensively in turbulence theory based on solar wind observations (e.g., Denskat et al. 1983; Goldstein et al. 1994; Leamon et al. 1998, 2000; Hamilton et al. 2008; Sahraoui et al. 2009). However, the observations of such LFWs have not been adequately explored in the solar wind except for shocks.

One notable exception appears in the PhD thesis of K. Behannon, who studied 69 cases of highly coherent polarized fluctuations in the frequency range of 0.01–10 Hz at 0.46–1 AU using Mariner 10 magnetic field data. These events have short durations, typically lasting only 1 or 2 minutes. They appear to be LH or RH polarized in the spacecraft frame. Behannon (1976) speculated that the LH waves were ICWs and the RH waves were electron whistlers. The latter speculation was made because the solar wind plasma data were unavailable for accurate Doppler shift conversion, and Behannon thought the wave frequency in the spacecraft frame (f_sc) must be lower than the frequency in the plasma frame (f_sw) for sunward-propagating ICWs. We know that the solar wind speed (V_p) is generally 5–10 times faster than the Alfvén speed (V_A), and the phase speed of ICWs can be estimated as V_A, thus the f_sc can be higher than f_sw for both sunward- and antisunward-propagating ICWs. Similarly, the LH and RH waves could be both intrinsically RH polarized magntosonic waves or be a mixture of ICWs and magnetosonic waves. With no plasma data available, Behannon (1976) proposed that these waves might be associated with instabilities driven by temperature anisotropy.

Tsurutani et al. (1994) reported 17 long intervals of electromagnetic waves with frequencies near the f_pc at 1 AU using the observations of the International Sun–Earth Explorer 3. The transverse peak-to-peak amplitudes of these waves are 1.5–5 nT, and the relative wave amplitudes (|δB|/B) are as large as 0.4 (Tsurutani et al. 1994). The waves are linearly or elliptically polarized in the spacecraft frame, and they are observed mostly when the interplanetary magnetic field (IMF) was along the Parker spiral (Tsurutani et al. 1994). Because Tsurutani et al. (1994) did not distinguish intermittent wave packets in the hours-long periods, not all of the events needed to be strictly waves. Because the waves are detected at or near the f_pc, Tsurutani et al. (1994) speculated that they were generated by the solar wind pickup of freshly created hydrogen ions, and the possible sources for the hydrogen were Earth's atmosphere, coronal mass ejections (CMEs), comets, and interstellar neutral atoms.

The launch of the Solar Terrestrial Relations Observatory (STEREO) provided an opportunity to observe these LFWs in regions far from any planetary or cometary influence (Kaiser et al. 2008). Jian et al. (2009) selected the LFWs based on the following three criteria. First, the transverse power is dominant. Second, the absolute value of ellipticity is larger than 0.7, meaning that the wave is nearly circularly polarized. Third, the percent polarization is larger than 70%, indicating that the signal-to-noise ratio is high. Jian et al. (2009) scrutinized 246 strong narrowband LFW events over 16 days using the high-resolution STEREO magnetic field data. They all have prominent enhancements of transverse power that is typically one or two decades higher than the compressional power. These LFWs are preferentially observed when the IMF is radial, and they propagate close to the IMF direction typically within an offset of 10° (Jian et al. 2009). In such case of parallel or quasi-parallel propagation, the possibility of mode conversion between LH and RH polarized waves is low.

Assuming that all of the LFWs are ICWs, i.e., they are LH polarized in the plasma frame, their LH polarity in the spacecraft frame indicates that they propagate along with the solar wind, the wave propagation vector k is antisunward, and k · V_p is positive. Alternatively, the observed RH polarity implies sunward-propagating k, so k · V_p is negative. Treating the LH and RH waves separately, Jian et al. (2009) converted the f_sc to f_sw by removing the Doppler shift effect:

$$\begin{eqnarray} f_{{\rm sc}} &=& f_{{\rm sw}} + \frac{{{\boldsymbol k} \cdot {\boldsymbol V}_{\!p} }}{{2\pi }} \approx f_{{\rm sw}} + \frac{{2\pi f_{{\rm sw}} \hat {\boldsymbol k}\cdot {\boldsymbol V}_{\!p} }}{{2\pi V_{\rm A} }} \nonumber \\ && \approx f_{{\rm sw}} \left({1 + \frac{{V_p }}{{V_{\rm A} }} \hat {\boldsymbol k}\cdot \hat {\boldsymbol V}_{\!p} } \right). \end{eqnarray} \tag{ 1 }$$

The average frequency of these waves is converted from 0.28 Hz in the spacecraft frame to 0.03 Hz in the plasma frame. Because the IMF is about 7 nT at 1 AU (e.g., p. 92 of Kivelson & Russell 1995), the f_pc and f_ec are about 0.1 and 200 Hz in the plasma frame, respectively. The f_sw of these LFWs is about a third of f_pc, consistent with the fact they have not yet been resonantly damped by the solar wind protons. In contrast, because the phase speed of the electron cyclotron waves is faster than the solar wind speed, the Doppler shift term does not dominate, and the f_sc can range from a fraction of 200 Hz to slightly over it, depending on k·V_p. This is consistent with the whistler wave frequency of 35 Hz from the turbulence studies by Sahraoui et al. (2009) and of 10–100 Hz from the wave observations by Breneman et al. (2010).

Jian et al. (2010) have investigated more than 600 similar LFW events over 12 days at 0.3 AU using the magnetic field data from the Mercury Surface, Space Environment, Geochemistry, and Ranging (MESSENGER) spacecraft and from Helios 1. Although the MESSENGER and Helios 1 observations were made more than 30 yr apart, the LFWs have similar characteristics. The wave power at 0.3 AU is stronger than at 1 AU, consistent with a stronger IMF intensity at 0.3 AU. The fractional wave amplitude is on average 0.03, and most of the f_sw fall in the range of 0.3–0.5 of the local f_pc, similar to the results at 1 AU (Jian et al. 2010).

Such waves near f_pc are extensively distributed in the solar wind, thus we may only have had glimpses of the "tip of the iceberg." We need to study them over a long period and consider the solar wind conditions and pickup ion sources. Because these LFWs tend to appear as clusters, we will refer to periods of extensive LFW activity as "LFW storms," in analogy with the mirror-mode storms for groups of mirror-mode waves (Russell et al. 2009). In this paper, we require the LFW storms to last longer than 10 minutes, and we describe a comprehensive search for them at STEREO A (STA) during 2008. In Section 2, we introduce the identification of LFW storms and obtain some statistical results on their properties. In Section 3, we compare the LH and RH wave storms and show rare cases in which two LFW storms of opposite polarities are observed closely. In Section 4, we study the solar wind conditions of these LFW storm periods, including α-particle parameters. In Section 5, we investigate whether they are related to the pickup of interstellar or cometary ions. Finally, we discuss and summarize our findings in Section 6.

We choose to study the data from STA because the interstellar pickup He⁺ flux (see Section 5) is presently available from STA and not from STEREO B. We confine the study to 2008, because STA was far from any planet and because 2008 was in the long and deep solar minimum 23/24 covering 2008–2009 (e.g., Bisi et al. 2011; Tsurutani et al. 2011). In 2008, the Sun and solar wind were quieter than in other years (e.g., Jian et al. 2011, 2013). In fact, only six interplanetary coronal mass ejections (ICMEs), 21 interplanetary shocks, 16 solar flares, and 5 low-energy-level solar energetic proton events are observed at STA in 2008, fewer than other years (e.g., Jian et al. 2013). These events are all marked in Figure 1.

Zoom In Zoom Out Reset image size

In order to survey an entire year of STEREO data efficiently, we use the magnetic field data with a time resolution of 1 s⁻¹, although the highest nominal resolution is 8 s⁻¹ (Acuña et al. 2008). Because the f_sc of these LFWs is generally below 0.5 Hz (Jian et al. 2009), the 1 s⁻¹ data with a Nyquist frequency of 0.5 Hz can resolve most of them. To find the LFW storms, we first plot the time series of magnetic field data. Second, as illustrated in Figure 2, we perform the dynamic spectrum analysis of the coherence between two transverse magnetic field components, which are B_T and B_N in the radial–tangential–normal (RTN) coordinate. The area with coherence lower than 0.5 is masked with black and excluded from further analysis. Third, we draw dynamic spectra of the transverse wave power and ellipticity. The dynamic spectrum analysis is performed for the magnetic field data in intervals of 12 hr. When we see an interval with an enhanced transverse power where the absolute value of the ellipticity is above 0.5 in an unmasked area, we take the fourth step to conduct the detailed wave analysis as described in Jian et al. (2009, 2010). Finally, we select the intervals satisfying the three wave criteria as introduced in paragraph 5 of Section 1, the same as in Jian et al. (2009, 2010), and record all of the wave parameters. The dynamic spectrum analysis is basically conducted with a fast Fourier transform (FFT) using Means (1972) quadrature spectrum technique and the wave analysis method described in Song et al. (1994). Details of these analyses are described in Means (1972), Song et al. (1994), and Jian et al. (2010).

Zoom In Zoom Out Reset image size

The long axis of the wave perturbation ellipse (I) is perpendicular to the B–k plane for an intrinsically LH polarized wave, and it is in the B–k plane for RH waves (Stix 1962; Lacombe et al. 1990; Blanco-Cano 1995). In Jian et al. (2009, 2010), we required the criterion that the long axis of the perturbation ellipse within 10° of the direction perpendicular to both B and k in order to approximate that I is perpendicular to the B–k plane. However, we should have required that I was parallel to the cross product of B and k to perform the proper test. Therefore, the test of the wave handedness was not precise. In this study we do not require I to be perpendicular to the B–k plane because the angle between I and the B–k plane varies widely from 0° to 90°.

In total, we have identified 1354 LFW events. Their durations range from tens of seconds to tens of minutes; and the majority last only a few minutes. We define the LFWs lasting longer than 10 minutes to be LFW storms, and 241 wave events are LFW storms, accounting for 17.8% of the LFW events registered in 2008. We note that a great number of isolated short-duration waves could have been missed because they cannot be resolved in the 12 hr blocks of our dynamic spectrum analysis. The LFW storms are observed cumulatively 0.9% of the year, fairly close to the results obtained from the scrutiny of individual wave packets in Jian et al. (2010), suggesting that the majority of LFW intervals occur in the form of storms and we do not miss much LFW activity in this study. Hence, the results of LFW storms are valid. The median of the relative wave amplitudes is 0.025 for LFW storms, similar to that of short-duration waves in Jian et al. (2010). Denoting the compressional ratio as the ratio of the compressional power to the transverse power, we find that the compressional ratio of these LFWs ranges from 0.004 to 0.268, with an average of 0.046. Therefore, the transverse power is on average more than 20 times stronger than the compressional power, and the LFWs are indeed transverse.

Figure 1 shows the distribution of LFW storms in a stack plot of solar wind speed for 27.27 day solar rotations of 2008. A majority of the LFW storms (marked by red bars) are observed in the trailing part of fast wind. The ICMEs, interplanetary shocks, and suspicious close encounters of comets are marked by yellow bars, green filled circles, and blue open circles, respectively. The former two are identified in Jian et al. (2013), whereas the comet encounter will be discussed in Section 5. The observations of LFW storms do not seem to be particularly associated with the above three types of events. Short-duration LFWs near the f_pc have been observed in ICMEs at times though. Two LFW storms happened to be observed within half an hour of shocks. We have removed them to avoid any confusion caused by whistlers or other LEWs driven by the shocks, which are studied separately by Aguilar-Rodriguez et al. (2011), Kajdič et al. (2012), Ramírez Vélez et al. (2012), and others.

Goldstein et al. (1985) observed LH polarized waves in the solar wind frame upstream of the Jovian bow shock and concluded that they were probably generated by resonant instability excited by bursts of relativistic electrons (∼MeV). Tsurutani et al. (1994) associated 12 of 17 wave events with energetic solar flare particle events. Hence, for this study, we check the solar flares and the solar energetic particle (Mewaldt et al. 2008) measurements from STA.

In total, 16 solar flares are detected by the Geostationary Operational Environment Satellite and the extreme ultraviolet imager (Howard et al. 2008) of STEREO (http://secchi.lmsal.com/EUVI/euvi_catalog.txt). They are marked by magenta crosses in Figure 1. Only one flare reached M-class. It occurred on 2008 March 25, but no associated LFW storm was observed on that day. No noticeable enhancements of relativistic energetic electrons (the energy needed to generate waves in such a frequency range) are detected by the high-energy telescope (von Rosenvinge et al. 2008) of STA in 2008, consistent with the fact that 2008 was in the deep solar minimum 23/24. There are no solar energetic proton events where the low-energy telescope (LET; Mewaldt et al. 2008) daily averaged intensity of 10–15 MeV protons exceeded 10⁻⁴ cm⁻² sr⁻¹ s⁻¹ MeV⁻¹ either. Using a lower energy level, we found five intervals when the 3 hr averaged 1.8–3.6 MeV proton rate exceeded 5 × 10⁻⁴ cm⁻² sr⁻¹ s⁻¹ MeV⁻¹, which are attributed to CMEs or flares (analyzed based on the preliminary list at http://www.srl.caltech.edu/STEREO/Level1/LET_public.html). They are denoted by the green horizontal bars at the top of each panel in Figure 1. From Figure 1, we can see that many LFW storms are observed when the energetic particle events are absent, ruling them out as the sources of these waves. In addition, as discussed in Tsurutani et al. (1994), the energetic particle events typically have broad power-law type velocity distributions and are not monoenergetic in nature, so it is hard to explain the narrow frequency range of these LFWs if they are caused by the energetic particles.

Using magnetic field data of 10 minute resolution, we calculate the acute angle between B and R and mark the intervals when the angle is ⩽10° as short blue bars in Figure 1. Because the B–R acute angle ⩽10° corresponds to |B_R/B| ⩾ 0.9848, we can define it as a "radial field." There is moderate overlap between radial field intervals and LFW storms. However, they are not one-to-one correlated. Not every LFW storm occurs in a radial field interval, and vice versa. This could be partly because the IMF is frequently changing its direction and partly because certain solar wind plasma conditions might be needed for these waves to grow. In addition, we note that the B–R acute angle ⩽10° does not occur often and has noticeably shorter duration than the near-radial field conditions, |B_R/B| > 0.9 (the B–R acute angle <25°), used in many other studies (e.g., Neugebauer & Goldstein 1997; Neugebauer et al. 1997; Jones et al. 1998; Wang et al. 2003; Orlove et al. 2013). Orlove et al. (2013) examined the intervals of such near-radial IMF lasting more than 6 hr from 14 yr in ecliptic observations at 1 AU and found they often appeared in rarefaction regions. Based on wind speeds and thermal ion compositions, Orlove et al. (2013) suggested that the solar wind surrounding the near-radial IMF comes from typical low-latitude sources that are nominally considered as slow-wind sources. The near-radial IMF is caused by either changing the wind speed associated with a fixed foot point of IMF or by moving the IMF foot point from one wind source to another, such as through interchange reconnection (e.g., Schwadron 2002; Gosling & Skoug 2002; Riley & Gosling 2007; Orlove et al. 2013).

Similar to the short-duration waves, the LFW storms can display LH and RH polarity in the spacecraft frame. Note that the polarization herein is defined based on the rotation of B fluctuations of the waves, analogous to the optical polarization. The plasma physics polarization (Stix 1962), expressed as the product of the magnetic helicity and cross helicity (Goldstein et al. 1985), cannot be obtained because there are no available electric field data or velocity data with the resolution comparable to that of the magnetic field data. This is a common drawback for solar wind data from interplanetary missions.

Among the 241 LFW storms, 133 (108) appear to be LH (RH) polarized in the spacecraft frame. The fraction of LH is 55%, consistent with the predominance of LH waves for short-duration LFWs in Behannon (1976) and Jian et al. (2009, 2010), although the predominance here is marginal. At 1 AU, the fraction of RH waves decreases moderately from 45% in wave storms to 36% in short-duration waves, possibly because the RH ones are damped more than the LH ones in their evolution from their generation in storms to their sporadic existence as short-duration wave packets.

In 14 cases, LH and RH storms are observed closely, i.e., are events whose intermediate time is separated by less than 1 hr. Figure 2 illustrates an example when two polarities are observed closely. It occurred on 2008 February 20 in the early declining part of a fast wind stream. Figure 2 shows (a) the time series of the magnetic field over 4 hr, and the dynamic spectra of (b) the coherence between B_T and B_N, (c) the transverse power spectral density, and (d) the ellipticity from the Means (1972) technique. In the period of A1–A2, the waves are LH polarized in the spacecraft frame and last for about 40 minutes. Half an hour later, the RH polarized waves emerge in the period of B1–B2 and last for approximately 40 minutes. We note that the two intervals are almost mirror images of each other in time and polarization. Through the detailed wave analysis, we find that during the RH wave period there are also simultaneous LH polarized waves at the lowest frequencies.

The classification of LH/RH polarization is supported by the hodograms of magnetic field in these two intervals, as shown in Figures 3 and 4. After converting B from RTN coordinates in panel (a) to the minimum variation analysis (MVA; Sonnerup & Cahill 1967) coordinates in panel (b) and removing the average field, we plot the hodograms of the magnetic field perturbations in panel (c). From panel (b), we can see B is mainly in the minimum variance K direction. The magnetic field perturbation is RH around K (therefore also B) in Figure 3 and LH around K and B in Figure 4, consistent with the polarization classification through the wave analysis (Means 1972; Song et al. 1994; Jian et al. 2010).

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

In addition, we examine the solar wind conditions during this 4 hr wave storm period. As displayed in Figure 5, in contrast with the neighboring solar wind, the proton temperature (T_p) in the LFW storm period is a little lower, whereas the proton bulk speed and number density (N_p) data are quieter with no substantial amplitude change. No correlated perturbations of B and N_p are detected in this 4 hr period, so these waves are not compressive magnetosonic waves. However, we can only examine up to the 1 minute cadence. Plasma and magnetic field data of higher cadence would help determine if there is any compressibility and help distinguish the magnetosonic/whistler waves and ICWs. In this 4 hr period, the IMF is primarily in the antisunward direction and does not change direction from the LH to RH storm. We do not see any apparent difference in the plasma conditions between the LH and RH storm periods except that the RH one has slightly lower T_p and β. Because V_p and V_A are respectively 600 and 50 km s⁻¹ in this interval, the Doppler shift effect is significant. As the solar wind approaches 600 km s⁻¹ at most times of the day, the distribution function gets truncated and α data have extensive gaps (K. Simunac (of the STEREO team) 2013, private communication), and thus the α data are not useful for this interval. In addition, there is no flare, and there are no energetic proton or electron events associated with this interval.

Zoom In Zoom Out Reset image size

In rare cases, the LH and RH polarities coexist and one polarity dominates, being either LH or RH. Figures 6 and 7 illustrate such an example on September 13 and 14. From Figure 6(d), we can see there are two bands of wave activity: one is LH spanning a wide frequency range, the other one is RH at a lower and narrower frequency range. Although the LFW activity lasts for about 3 hr, we can only find a short interval where LH and RH waves are observed in the same power spectrum and both meet the three wave criteria mentioned earlier. Figure 7 displays such a wave packet, which lasts for about 4 minutes. The RH polarized wave has an ellipticity of −0.89 and a percent polarization of 90%, propagating 88 away from the IMF; the LH polarized wave has an ellipticity of 0.88 and a percent polarization of 96%, propagating 23 away from the IMF. The LH wave is stronger and at higher frequency than the RH wave.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

This event occurred near the rear edge of a long-lasting fast wind. As illustrated in Figure 8, at the time of the LFW storm, the solar wind is slow at a speed of 360 km s⁻¹, whereas the N_p, T_p, and β are quieter and lower than most of the background solar wind. The α-particle data are unavailable in this event. In contrast with the previous storm example, the V_A is 78 km s⁻¹ and V_p/V_A is less than 5 in this interval. Again, no flare or energetic particle event is found to be associated with this LFW storm. Carefully investigating the events of LH/RH close occurrence or coexistence can benefit the understanding of these LFWs. Because such a study needs better plasma data coverage and sensible theoretical assumptions, we will conduct a separate study on this.

Zoom In Zoom Out Reset image size

In Figure 2, the LFW storms have a lower cutoff at about twice of f_pc, which is indicated by the white line at 0.06 Hz. In Figure 6, the RH wave storm has a lower cutoff near f_pc. Next we examine how the lower cutoff frequencies are distributed with respect to f_pc. When we conduct wave analysis of each power spectrum, we visually delineate a frequency range enclosing the peak of transverse power. The two short dotted horizontal lines in Figure 7(b) denote such frequency ranges chosen for the RH and LH polarized waves. The minimum of the frequency range is called f_min. Meanwhile, for each storm, a program is set to automatically search the two closest frequencies where the transverse power is at half of the peak. The lower half-power frequency is denoted as f₁, also marked in Figure 7(b). The histograms of f_min/f_pc and f₁/f_pc are analogous, as illustrated in Figure 9. The majority of the two ratios fall in the range of 1–4, indicating that the lower cutoff frequencies of the wave spectra are approximately 1–4 times of f_pc. This suggests that these waves are unlikely to be generated by local pickup protons because, if so, they would have lower cutoff frequency at f_pc (e.g., Murphy et al. 1995; Cannon et al. 2013). The possibility of the association with other local pickup ions is even lower because their cyclotron frequencies are lower than f_pc.

Zoom In Zoom Out Reset image size

Although most of the LFW storms are observed in the trailing part of the fast wind, the solar wind speed ranges widely from 250 to 750 km s⁻¹, with a median speed below 400 km s⁻¹, as shown in Figure 10(e). This is consistent with the association of near-radial field and low-latitude slow-wind sources in Orlove et al. (2013). In Figure 10, we compare the histogram distributions of solar wind parameters between LFW storm periods (in red) and all solar wind (in blue) during 2008 (left) and obtain the relative occurrence rate in LFW storms normalized by the rate in general solar wind (right). The plasma data of 1 minute resolution are from the plasma and supra-thermal ion composition investigation (PLASTIC; Galvin et al. 2008) on the STEREO spacecraft.

Zoom In Zoom Out Reset image size

In contrast with the general solar wind, the LFW storm period has a smaller B–R acute angle, a slightly slower V_p, a smaller N_p, a cooler T_p, and a lower β. The smaller B–R acute angle indicates the LFW storms are preferentially observed when the IMF is more radial than the nominal Parker spiral, consistent with the conclusions in Behannon (1976) and Jian et al. (2009, 2010). The B–R acute angles are mainly 6°–36° in reality, whereas the normalized distribution peaks within 6°. We cannot detect the LFW in every radial IMF interval. This might be because the IMF is constantly changing direction or some specific set of solar wind conditions is needed for these waves to grow.

The proton double streams and proton–α differential streaming are persistently observed in the solar wind (e.g., Feldman et al. 1973a, 1974; Marsch et al. 1982a; Marsch & Livi 1987; Neugebauer et al. 1996; Steinberg et al. 1996). Such relative drifts may be related to these LFWs by enhancing the ion beam formation that can create RH magnetosonic waves and by changing the resonant condition for wave–particle interactions (e.g., Daughton & Gary 1998; Hu & Rifai Habbal 1999; Gary et al. 2000; Marsch 2006; Maneva et al. 2013; Verscharen et al. 2013; Verscharen & Chandran 2013). No proton beam distribution is available yet from STEREO. We next consider the solar wind conditions with respect to α-particles, using α data of 10 minute resolution, the highest cadence available for STA at present. Because the standard processing of α data has a cutoff when the speed of α-particles (V_α) reaches around 600 km s⁻¹, the α data are available for about 58% of the time in 2008 and for only about 18% of the LFW storm periods (87 data points in total).

Figure 11 displays the histogram comparison of α-particle-related solar wind parameters between LFW storms (in red) and all solar wind (in blue) during 2008 and the normalized occurrence rate in LFW storms. In contrast with the general solar wind, the LFW storms have a faster differential flow between α-particles and protons normalized by Alfvén speed (|V_α − V_p|/V_A), a higher density abundance ratio between α-particles and protons (N_α/N_p), and a higher temperature ratio between α-particles and protons (T_α/T_p). The α-particle speed is used because its velocity is unavailable. The results suggest that the LFW storms might be related to α beams.

Zoom In Zoom Out Reset image size

However, the significance of the above results could be compromised by the limitation of the one-dimensional (1D) Maxwellian fit used to calculate moments for protons and α-particles in PLASTIC. Because temperature anisotropy of solar wind protons is ordered by the magnetic field, with no change at all in the plasma, as the IMF direction changes, the 1D fit will look at a varying pitch angle and hence see a different temperature. In fast wind, the T_p is higher in the direction perpendicular to IMF than in the parallel direction (e.g., Marsch et al. 1982b; Kasper et al. 2002; Hellinger et al. 2006; Bale et al. 2009; Maruca et al. 2011). When the IMF is radial, the measured T_p will be T_//, which can be lower than the T_p in other field conditions. In addition, as the differential flow of α-particles is usually along the magnetic field, the measured differential flow speed will be faster in a radial field than in other field conditions. Hence, the correlation of LFW storms with cooler T_p, lower β, and faster |V_α − V_p|/V_A needs further confirmation using another data set built on two-dimensional (2D) fits.

One proposed mechanism of the LFW generation is associated with pickup ions, which are in fact distributed extensively in the heliosphere. The pickup ions at 1 AU can originate from interstellar neutral gas (e.g., Fahr 1974; Möbius et al. 1985; Gloeckler et al. 1998), dust in the inner heliosphere (e.g., Fahr et al. 1981; Geiss et al. 1995; Schwadron et al. 2000; Wimmer-Schweingruber & Bochsler 2003), or cometary nuclei (e.g., Johnstone 1990; Neubauer et al. 1993).

For interstellar hydrogen atoms, the radiation pressure is greater than the gravitation, so a cavity devoid of them forms around the Sun (Thomas 1978; Fahr 1978); in addition, they are typically ionized outside 1 AU. For all other interstellar neutral species, the gravitation is greater, thus the neutral gas is focused on the downwind side of the Sun relative to the interstellar medium; this is called the focusing cone (Fahr 1974). In contrast, the inner-source pickup ions do not have any gravitational focusing cone.

Using the solar wind section of the PLASTIC suite, Drews et al. (2010) studied heavy pickup ions at STA during 2007–2008 and found that He⁺ and Ne⁺ enhancements concur in the focusing cone whereas the other species (C⁺, N⁺, O⁺, and the H₂O⁺ group) are evenly distributed throughout 2007–2008, shown in Figure 3 of Drews et al. (2010). The rise of pickup C, N, O, and H₂O group ions is absent during focusing cone passages, suggesting that these ions at STA orbit are likely to originate from the inner source (Drews et al. 2010). In fact, because of lower first ionization potentials than He and Ne, the neutrals of C, N, O, and H₂O groups from interstellar sources would have been ionized much farther out in the heliosphere (Drews et al. 2010).

Because the focusing cones of the interstellar pickup He⁺ and Ne⁺ are the same (Drews et al. 2010), we use He⁺ to represent both species in the following. There are four speed ranges for He⁺ measurement at STEREO: 1.45–1.85, 1.85–2.5, 2.5–3.5, and 3.5–10 of V_p. Because the pickup He⁺ would have an energy cutoff (in the spacecraft frame) at about twice V_p (four times the solar wind energy), we use the first range, 1.45–1.85 of V_p, for the pickup He⁺. To match LFW storm durations, we use He⁺ data of 10 minute resolution, the highest cadence available from STEREO. The count rate of He⁺ has been corrected for efficiencies and the ICW storm duration.

Because STA is constantly drifting away from the Earth, the observed focusing cone of the interstellar pickup He⁺ is in October and November of 2008 as shown in Figure 12(a), consistent with Drews et al. (2010). However, the monthly occurrence number and cumulative duration of LFW storms do not maximize in the focusing cone, as shown in Figures 12(b) and (c). Instead, they peak in April and have high values in September and December. The monthly event number and cumulative duration of LFW storms have correlation coefficients of 0.25 and 0.0068 with the monthly flux of pickup He⁺, respectively. The correlation coefficient between the transverse wave power and pickup He⁺ flux is only 0.19. All of these facts suggest that these LFW storms are unlikely to be associated with interstellar pickup He⁺ or Ne⁺. However, we cannot completely rule out any possible correlation with pickup ions originating from the inner source because these ions are evenly distributed in time at 1 AU.

Zoom In Zoom Out Reset image size

As demonstrated in Figures 12(b) and (c), the event number and cumulative duration of LFW storms vary significantly from month to month, by a factor of six. We investigate whether there is any other factor affecting their distributions. First, the distributions of LFW storm number and cumulative duration maximize in 2008 April, when Mercury, Venus, and Mars were all far from the Sun–STA line and the Parker spiral line connecting the Sun and STA, precluding any particular contribution from these planets.

Second, we examine the occurrence of comets in the inner heliosphere in 2008. There were tens of Sun-grazing comets observed by Solar and Heliospheric Observatory (SOHO) and STEREO in 2008 (see http://sungrazer.nrl.navy.mil/index.php and http://www.rkracht.de/secchi/comets.htm). Their orbits generally have a small aphelion (within 0.1 AU) and a high inclination, so these comets spent only a couple of days in the ecliptic plane. The count of comets in 2008 April was less than in several other months in 2008. Among the few Sun-grazing comets with unusually low inclination, we find that only C/2008 H9 (SOHO) was close to the Sun–STA line when it was in the ecliptic plane and its aphelion was 0.005 AU. In addition, using the small-body database search engine of the Jet Propulsion Laboratory (http://ssd.jpl.nasa.gov/sbdb_query.cgi), we find 14 other comets whose perihelia were within 1 AU and passed in 2007–2009. The search window was extended beyond 2008 to include comets that could come inside 1 AU but do not reach aphelia in 2008. There are three comets that might have a relatively close encounter with STA, and they are C/2008 J4 (McNaught), C/2007 W1 (Boattini), and 207P/NEAT. The time of the close approach with STA or the Sun–STA line of the above four comets is marked as blue open circles in Figure 1. We do not see more LFW storms in the vicinity of possible comet encounters. Moreover, the waves triggered by a comet should be primarily associated with water group ions (e.g., Tsurutani & Smith 1986; Mazelle & Neubauer 1993; Coates et al. 1993; Tsurutani et al. 1995) and of higher amplitude (e.g., Tsurutani & Smith 1986; Neubauer et al. 1993; Tsurutani et al. 1995). Similar speculation and disapproval of the comet association with LFWs were also made earlier when the International Cometary Explorer spacecraft observed this type of waves at 0.19 AU away from the comet P/Halley in Tsurutani et al. (1987).

Third, because the LFW storms are preferentially observed when the IMF is radial, we examine the time fraction of radial field in each month. From Figure 12(d), we can see that the monthly distribution of such a time fraction mimics the distribution of the cumulative ICW storm durations. The two have a correlation coefficient of 0.71. If we loosen the field condition to |B_R/B| > 0.9 as mentioned in Section 2, the correlation coefficient decreases to 0.47. In 2008, the IMF is within 10° of the radial direction for 0.95% of the time, nearly equivalent to the time fraction of LFW storms (0.9%), implying that these waves could be ubiquitous in the solar wind and that they are observed occasionally mainly because of the constantly varying IMF geometry. In fact, using the observed B–V angle distribution of magnetic helicity, He et al. (2011) demonstrated that the ICWs coexist with obliquely propagating kinetic Alfvén waves or whistler waves in the solar wind.

Coherent transverse electromagnetic waves near f_pc have been observed in the inner heliosphere from 0.3 to 1 AU (Behannon 1976; Tsurutani et al. 1994). Using specific criteria, Jian et al. (2009, 2010) scrutinized hundreds of LFW packets at 1 and 0.3 AU. Their average duration is only tens of seconds. However, these wave packets tend to appear in clusters, and the wave activity can last a few minutes to tens of minutes, consisting of many intermittent wave packets. Requiring that the LFW storms last longer than 10 minutes, we have found 241 events at STA in 2008. Cumulatively, they are observed 0.9% of the time, similar to the time fraction of the LFWs if we scrutinize short-duration wave packets individually (Jian et al. 2009, 2010). This suggests that the majority of LFWs are in storms and we have not missed much wave activity by inspecting only LFW storms. Through this extensive survey, we have reached the following conclusions.

• 1.  
  The characteristics of the LFWs are similar whether they are in storms or isolated wave packets. The relative wave amplitude remains about 0.03, same as the amplitude at 0.3 AU. The LFWs may be constantly generated and dissipated in the solar wind throughout the inner heliosphere.
• 2.  
  The average f_sc of these waves is 0.178 ± 0.005 Hz, and the median f_sc is 0.169 Hz. The average and median f_sc/f_pc are 3.4 and 3.0, respectively. Because V_p is generally 5 to 10 times V_A and k is at a small angle of ${\boldsymbol V}_{\!\boldsymbol p}$, we can use Taylor's hypothesis 2π f_sc ≈ kV_p (Taylor 1938) to derive the approximate wavenumber k of 0.0024 km⁻¹ and ρ_pk of 0.27, where ρ_p is the proton inertial length (or skin depth).
• 3.  
  Many LFW storms are observed when there are no ICMEs, shocks, flares, or solar energetic particles. This suggests that ICMEs, shocks, flares, and solar energetic particles are unlikely to be the sources of the large population of these LFWs.
• 4.  
  For most LFW storms, the lower cutoff frequency of the wave spectra is about one to four times f_pc, different from the waves associated with parallel pickup of interstellar hydrogen in Ulysses observations (Murphy et al. 1995; Cannon et al. 2013), which have a cutoff at local f_pc, indicating that these LFWs are unlikely to be generated by local pickup ions.
• 5.  
  The occurrence of LFW storms does not peak in the focusing cone of interstellar pickup He⁺ and Ne⁺, suggesting that the two species do not contribute to the waves. However, we cannot preclude any correlation with inner-source pickup ions, because these pickup ions do not have a focusing cone at 1 AU and they are uniformly distributed in ecliptic longitudes.
• 6.  
  We have found four cases in which comets are close to the STA or Sun–STA line in 2008, but none of them seems to trigger these LFWs observed at STA. Because STA reached the regions far away from any planet, planetary sources are improbable too.
• 7.  
  The IMF is within 10° of the radial direction for 0.95% of the time in 2008, almost equal to the time fraction of LFW storms. The monthly distributions of cumulative LFW storm time and radial-IMF time fractions are correlated well. This indicates that the LFWs are preferentially observed when the IMF is more radial than usual, consistent with Jian et al. (2009, 2010). Because the LFWs propagating along the magnetic field have the least damping (e.g., pp. 128 and 147 of Gary 1993) and they are also carried by the solar wind, which is almost radial, the damping is at a minimum only when the field keeps radial from generation to observation site.

So far, we have ruled out the ICMEs, interplanetary shocks, solar energetic particles, comets, planets, and interstellar ions as the specific drivers of these extensively distributed LFWs. However, it remains a mystery how these waves are generated and whether they are generated locally or remotely. Because the solar wind speed is much faster than the wave phase speed, these LFWs cannot be generated outside 1 AU and propagate inward. So, if they are generated remotely, the question is how far inward.

In the solar wind, the nonthermal effects such as bulk flow inhomogeneities are associated with the origin of the observed proton (ion, in an extended sense) anisotropy (Feldman et al. 1973b). Temperature anisotropy and a secondary component (beam) of protons and α-particles are persistently observed in the solar wind (e.g., Feldman et al. 1974; Bame et al. 1975; Marsch et al. 1982a, 1982b). The proton temperature is larger perpendicular (T_⊥) than parallel to the magnetic field (T_//) in fast wind, and larger parallel than perpendicular in low- and intermediate-speed solar wind (e.g., Marsch et al. 1982b; Kasper et al. 2002; Hellinger et al. 2006, Bale et al. 2009; Maruca et al. 2011). How to generate such anisotropy is a fundamental question for a kinetic model of solar wind. Several mechanisms have been proposed using ion cyclotron dissipation (e.g., Isenberg & Vasquez 2007, 2009, 2011), stochastic demagnetization of ion gyro-orbits (e.g., Chandran et al. 2010, 2013), or ponderomotive force due to wave pressure gradients of phase-steepened Alfvén waves (e.g., Tsurutani et al. 2002). However, no definite answer has been reached yet.

When ion T_⊥ is greater than T_// and plasma β is low, the ion cyclotron anisotropy instability grows fast at k × B = 0 (e.g., Kennel & Petschek 1966; Leubner & Viñas 1986; p. 128 of Gary 1993). When ion T_// is greater than T_⊥ and the plasma β is large, the ion fire hose instability grows fast and generates magnetosonic/whistler waves (e.g., Kennel & Petschek 1966; Gary et al. 1985; p. 127 of Gary 1993). For fast wind, the former instability is found to be typical, whereas the latter one is found less often (e.g., Leubner & Viñas 1986). Both of the two types of instabilities act as regulating mechanisms on the shape of solar wind ion distribution functions (e.g., Leubner & Viñas 1986; Gary 1993; Gary et al. 2000; Tu & Marsch 2002; Hellinger et al. 2006; Bale et al. 2009; Bourouaine et al. 2010; Maruca et al. 2011; Kasper et al. 2013). Remotely in the solar corona, there are highly anisotropic heavy-ion distributions from SOHO ultraviolet coronagraph spectrometer observation (e.g., Kohl et al. 1998; Cranmer et al. 1999; Antonucci et al. 2000), and models have been created to produce such anisotropy (e.g., Cranmer & van Ballegooijen 2003; Hollweg 2008). Such temperature anisotropy and very low β in the corona would favor the growth of ICWs too (e.g., Omidi et al. 2014).

Furthermore, we consider a secondary ion population besides the core. When the ion velocity distributions have a ring or ring-beam character perpendicular to the background magnetic field, the ion cyclotron ring instability grows and generates ICWs (e.g., Lee & Birdsall 1979a, 1979b; Simons et al. 1980; Roth & Hudson 1985; Convery & Gary 1997). When the ion beam is relatively isotropic and cool, the ion beam instability grows faster and generates RH waves. The former applies to the ICWs in various planetary and cometary environments (e.g., Fraser 1985; McClements & Dendy 1993; Neubauer et al. 1993; Huddleston et al. 1998; Leisner et al. 2006; Russell & Blanco-Cano 2007), when free energy is provided by newborn pickup ions. The latter is often applied to the upstream and downstream waves of shocks (e.g., Barnes 1970; Russell et al. 1971; Fairfield 1974; Paschmann et al. 1979; Hoppe & Russell 1983; Tsurutani & Smith 1984; Smith et al. 1984; Viñas et al. 1984). Because we have ruled out many energy sources for ion beams, the remaining possibility for the LFWs would be inner-source pickup if there is energy input beyond the solar wind inhomogeneities.

Through our survey, these LFW storms are often found in the trailing part of fast wind. They are likely to be generated by the temperature anisotropy (T_⊥ greater than T_//), which is often found in fast wind; the radial field further allows the least damping of these LFWs. However, the existence of ion beams especially in the radial field condition complicates the scenario. In addition, the long duration near the radial field tends to occur in the rarefaction region after fast wind (Orlove et al. 2013), so it is hard to determine how critical the fast wind really is for the wave growth. In contrast with general solar wind, the LFW storms have lower N_p, cooler T_p, lower β, higher |V_α − V_p|/V_A, higher N_α/N_p, and higher T_α/T_p. The 1D Maxwellian fit could result in lower T_p, lower β, and higher |V_α − V_p|/V_A when IMF is radial, so this correlation needs further investigation using the data from a 2D fit.

In Figure 13, we compare the histograms of the wave properties between LH (in blue) and RH (in red) polarized LFW storms in the spacecraft frame, where the median values are denoted by the dashed lines. Because the waves near f_pc can be ICWs, magnetosonic/whistler waves, or a mixture of the two, we consider three scenarios to remove the Doppler shift effect and derive f_sw from f_sc: (1) all of the waves are ICWs, and the LH/RH waves are due to the Doppler shift of antisunward/sunward-propagating ICWs; (2) all of the waves are magnetosonic/whistler waves, and the LH/RH waves correspond to the sunward/antisunward propagation; and (3) all of the waves propagate along with the solar wind, and there is no polarity reversal.

Zoom In Zoom Out Reset image size

The average wave power of LH and RH waves is 0.014 ± 0.002 (mean ± the probable error of the mean) and 0.008 ± 0.001 nT², respectively. The average f_sc for LH and RH waves is 0.189 ± 0.006 and 0.163 ± 0.008 Hz, individually. In contrast with RH waves, the LH waves have slightly stronger power and higher f_sc. The propagation angles and f_sc/f_pc are similar between LH and RH waves. The propagation angles are mainly within 10°, indicating parallel propagation. These results are consistent with the results at 0.3 AU shown in Figure 4 of Jian et al. (2010). They can be explained by the first scenario that all of the waves are ICWs, because in this scenario, it would take a shorter time for antisunward-propagating waves (LH) to reach the spacecraft than the sunward ones (RH), and the LH waves are damped less, resulting in a stronger power, as shown in the scatter plot of wave power versus f_sw/f_pc in Figure 14(a). In the second scenario where all of the waves are magnetosonic/whistler waves, the antisunward-propagating waves (RH) would be stronger, contradicting the observation in Figure 14(b). However, the second and third scenarios can explain why a small number of waves have f_sw above f_pc. Another reason could be that our simplified Doppler shift differs from the actual frequency change in the nonuniform solar wind.

Zoom In Zoom Out Reset image size

The histogram distributions of f_sw and f_sw/f_pc in Figures 13(e)–(j) do not vary much with the scenario, consistent with the fact that V_p is much faster than V_A and the Doppler shift term in Equation (1) dominates. The majority of f_sw/f_pc fall in the range of 0.2–0.8 (Figure 13), and the ones with high power are in the range of 0.3–0.5 (Figure 14), close to the ratio derived from the LH ion cyclotron anisotropy instability and RH ion beam instability (e.g., Gary 1993). The f_sw/f_pc from ion fire hose instability would be higher, so the waves are unlikely to be driven by ion fire hose instability.

Furthermore, we compare the LFW storms inspected here with the LFWs studied in Jian et al. (2010) using MESSENGER observations at 0.3 AU. The radial variations of f_sc, f_sc/f_pc, f_sw, and f_sw/f_pc from 0.3 to 1 AU are displayed in Figure 15. Because the f_sw and f_sw/f_pc do not change much with the scenarios, we assume all waves are ICWs to remove the Doppler shift. Both f_sc and f_sw shift significantly to lower frequencies, from 0.3 to 1 AU, consistent with the decreasing IMF intensity. This indicates that most waves at 0.3 AU have been damped before reaching 1 AU, and the majority (if not all) of the LFWs observed at 1 AU are born after 0.3 AU, whether the waves are generated in a frame stationary with respect to the spacecraft (in the inner-source pickup scenario, f_sc would be constant) or to the solar wind (through plasma instabilities, f_sw would be constant). In the inner-source pickup scenario, the f_sc/f_pc will be close to 1 for newborn proton cyclotron waves and smaller than 1 for waves associated with other ions. The expansion of the distributions of f_sc/f_pc and their shift to higher values imply that many waves could be born in regions closer to the Sun than 0.3 AU. On the other hand, from 0.3 to 1 AU, the histogram distribution of f_sw/f_pc broadens and the dominance of the range of 0.3–0.4 weakens, possibly because the LFW growth is stronger at 0.3 AU than at 1 AU, supported by greater perpendicular temperature anisotropy (T_⊥/T_//) and lower β at 0.3 AU than at 1 AU (Marsch et al. 1982b; Matteini et al. 2007). However, the mechanism needs to answer why the relative wave amplitude remains roughly constant (about 0.03) across this large distance.

Zoom In Zoom Out Reset image size

As f_sw/f_pc approaches 1, the solar wind protons will cyclotron resonate with ICWs that are LH polarized, absorb the wave energy, and get heated. This is probably why the proton temperature in fast wind declines less with distance than in slow wind (Marsch et al. 1982b). For the waves that are RH polarized in the solar wind frame, because ion beams move faster than the solar wind, they would overtake these waves, observe them as LH polarized waves, resonate with them and get heated. In either case, these waves can play an important role in modulating the solar wind ion distribution and contribute to the heating and acceleration of solar wind.

The above results suggest that electromagnetic waves near the f_pc may be continuously generated and dissipated in the inner heliosphere, and they could be prevalent in the solar corona. The Solar Probe Plus and Solar Orbiter missions flying close to the Sun will probably observe them more frequently because the anisotropic ion distributions are greater, the ion beams are more energetic, and the magnetic field is more radial there. Plasma instabilities change greatly with parameters such as temperature anisotropy, drift speed, β, and so on, and solar wind conditions are variable. We plan to study these LFWs using the data from Wind and other spacecraft to determine their intrinsic polarity in the plasma frame and to check the associated ion velocity distributions, from which the temperature anisotropy and ion beam characteristics can be derived. Coordinating the observations with theory, we will try to find out the generation mechanism(s) of these LFWs. In rare cases, the LH and RH wave storms are observed closely or even concurrently. We will analyze such events in detail in another study to learn more about their generation and evolution.

This work is supported by NASA grants NNX13AI65G and NNX12AB29G and by NASA's STEREO mission, through IMPACT (Contract NAS5–00133) and PLASTIC (Contract NAS5–00132). We thank the STEREO/PLASTIC team for providing the plasma data. Jian thanks S. P. Gary for the helpful discussion and H. R. Lai and Y. D. Jia for assisting with the comet catalog. Isenberg is supported by NASA grants NNX11AJ37G and NNX13AF97G and NSF grant AGS0962506.