Absolute robotic GNSS antenna calibrations in open field environment

Abstract

We consider robotic calibrations of GNSS receiving antennas in an open field environment. At the newly built test range, the sky is unobstructed down to 10° elevation; an industrial robot with six degrees of freedom is employed. The antenna calibration algorithm uses single differences of carrier phases. Two types of antennas are tested, a common choke ring ground plane antenna and a rover-type antenna. Three types of errors are analyzed in detail: far-field multipath, near-field multipath, and errors of antenna positioning by the robot. For far-field multipath, it has been shown that the notion of the satellite signal reflection by the plain surface underneath the antenna fits well with the observed data. Parallel vertical antenna displacements are analyzed to decrease the test time. It has been shown that the near-field multipath originating from the body of the robot is the main contribution to the remaining error of calibrations: while error components related to the remaining far-field multipath and inaccuracies in the geometry of the installation are estimated at 0.1 mm each, the overall accuracy of achieved calibrations is estimated as 0.3 mm for choke ring-type antenna and as 0.7 mm for rover-type antenna. A comparison of the obtained calibrations with Geo++^® GmbH data is provided.

Appendices

Appendix 1: Calculation of covariance matrices of measurement errors

The diagonal covariance matrices $Q_{j,p}$ in (8) characterize the total measurement errors $E_{j,p} + M_{j,p}$. Their elements are determined as a function of three variables, the satellite elevation angle in the local coordinate system $\theta_{r}$, satellite elevation angle in the frame of the tested antenna $\theta_{t}$, and the tilt angle of the tested antenna $\theta_{i}$. A second-degree polynomial in the three variables is used to represent these functions

$$ \sigma^{2} \left( {\theta_{r} ,\theta_{t} ,\theta_{i} } \right) = a_{11} \theta_{r}^{2} + a_{22} \theta_{t}^{2} + a_{33} \theta_{i}^{2} + a_{12} \theta_{r} \theta_{t} + a_{23} \theta_{t} \theta_{i} + a_{13} \theta_{t} \theta_{i} + a_{1} \theta_{r} + a_{2} \theta_{t} + a_{3} \theta_{i} + a $$

(22)

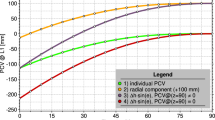
To define coefficients, the set of Equation (7) was solved primarily in the assumption that $Q_{j,p} = I$, where $I$ is the unit matrix. Then, the squares of the obtained residuals were approximated by the polynomial (22). It should be noted that from experiments, it was found that the solution of the same problem with equally weighted measurements, which correspond to unit covariance matrices $Q_{j,p}$, is slightly different from the case of the weighted measurements discussed in this study. However, the difference in PCC in both cases does not exceed 0.5 mm.

Appendix 2: Equivalency of the methods of time-differenced single differences and single differencing

We take a specific satellite. The observation equations for TDSD are as follows

$$ G \cdot A \cdot X = G \cdot \Delta \varPhi + G \cdot \varepsilon $$

(23)

where

$$ G = \left( {\begin{array}{*{20}c} 1 & { - 1} & {} & {} & {} \\ {} & 1 & { - 1} & {} & {} \\ {} & {} & \ddots & \ddots & {} \\ {} & {} & {} & 1 & { - 1} \\ \end{array} } \right)_{{\left( {m - 1 \times m} \right)}} $$

$$ A = \left( {\begin{array}{*{20}c} {Y_{1}^{{ - 1}} \left( {\theta _{1} ,\alpha _{1} } \right)} & {Y_{1}^{0} \left( {\theta _{1} ,\alpha _{1} } \right)} & \cdots & {Y_{L}^{L} \left( {\theta _{1} ,\alpha _{1} } \right)} \\ {Y_{1}^{{ - 1}} \left( {\theta _{2} ,\alpha _{2} } \right)} & {Y_{1}^{0} \left( {\theta _{2} ,\alpha _{2} } \right)} & \cdots & {Y_{L}^{L} \left( {\theta _{2} ,\alpha _{2} } \right)} \\ \vdots & {} & \ddots & \vdots \\ {Y_{1}^{{ - 1}} \left( {\theta _{m} ,\alpha _{m} } \right)} & {Y_{1}^{0} \left( {\theta _{m} ,\alpha _{m} } \right)} & \cdots & {Y_{L}^{L} \left( {\theta _{m} ,\alpha _{m} } \right)} \\ \end{array} } \right)_{{\left( {m \times m} \right)}}$$

and $\Delta \varPhi = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\Delta \varphi_{1} } \\ {\Delta \varphi_{2} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ {\Delta \varphi_{m} } \\ \end{array} } \\ \end{array} } \right)_{\left( m \right)}$ are single-phase differences between the tested and reference antennas.

$X$ is the vector of the sought expansion coefficients for tested antenna PCC in spherical harmonics, the angles $\theta_{i}$ and $\alpha_{i}$ are the zenith and azimuth of a satellite in the tested antenna frame for the ith measurement, and $\varepsilon$ is the vector of measurement errors.

The measurement errors are considered uncorrelated with the diagonal covariance matrix $\varepsilon$. Let the matrix be a unit matrix. Then, the covariance matrix of random vector $G\varepsilon$ is determined in accordance with the law of error distribution as follows: $\varSigma_{G\varepsilon } = G\varSigma_{\varepsilon } G^{\text{T}} = GG^{\text{T}}$, the matrix of weight coefficients of the LSM will then be $P = \left( {GG^{\text{T}} } \right)^{ - 1}$, and the normal equations of the LSM for observation Equation (23) can be written

$$ A^{\text{T}} G^{\text{T}} \left( {GG^{\text{T}} } \right)^{ - 1} GA \cdot X = A^{\text{T}} G^{\text{T}} \left( {GG^{\text{T}} } \right)^{ - 1} G \cdot \Delta \varPhi $$

(24)

The matrix $GG^{\text{T}}$ is symmetric, three-diagonal, and looks like this

$$ GG^{\text{T}} = \left( {\begin{array}{*{20}c} 2 & { - 1} & {} & {} & {} \\ { - 1} & 2 & { - 1} & {} & {} \\ {} & { - 1} & \ddots & \ddots & {} \\ {} & {} & \ddots & 2 & { - 1} \\ {} & {} & {} & { - 1} & 2 \\ \end{array} } \right)_{{\left( {m - 1} \right) \times \left( {m - 1} \right)}} $$

(25)

The inverse is (Hu and O’Connell 1996)

$$ \left( {GG^{\text{T}} } \right)^{ - 1}_{i,j} = \frac{{\left( {i + j - \left| {i - j} \right|} \right)\left( {2m - \left| {j - i} \right| - i - j} \right)}}{4m} $$

(26)

Then

$$ G^{\text{T}} \left( {GG^{\text{T}} } \right)^{ - 1} G = I_{{\left( {m \times m} \right)}} - \frac{1}{m}{\text{e}}_{m} {\text{e}}_{m}^{\text{T}} $$

(27)

where ${\text{e}}_{m}$ is the vector of dimension m consisting of units

$$ {\text{e}}_{m} = \left( {\begin{array}{*{20}c} 1 \\ \vdots \\ 1 \\ \end{array} } \right)_{\left( m \right)} $$

From (27), the expansion coefficients of the PCC and the related covariance matrix for the TDSD algorithm are

$$ \begin{aligned} \varSigma_{{x,{\text{sddt}}}} & = \left( {A^{\text{T}} G^{\text{T}} \left( {GG^{\text{T}} } \right)^{ - 1} GA} \right)^{ - 1} = \left( {A^{\text{T}} \left( {I - \frac{1}{m}{\text{e}}_{m} {\text{e}}_{m}^{\text{T}} } \right)A} \right)^{ - 1} \\ X_{\text{sddt}} & = \left( {A^{\text{T}} G^{\text{T}} \left( {GG^{T} } \right)^{ - 1} GA} \right)^{ - 1} A^{\text{T}} G^{\text{T}} \left( {GG^{\text{T}} } \right)^{ - 1} G \cdot \Delta \varPhi \\ & = \left( {A^{\text{T}} \left( {I - \frac{1}{m}{\text{e}}_{m} {\text{e}}_{m}^{\text{T}} } \right)A} \right)^{ - 1} A^{\text{T}} \left( {I - \frac{1}{m}{\text{e}}_{m} {\text{e}}_{m}^{\text{T}} } \right) \cdot \Delta \varPhi \\ \end{aligned} $$

(28)

Expressions (28) define the solution of observation equations for the TDSD method.

Next, consider the SD algorithm. To estimate the PCC, the multipath errors of the reference antenna, and the firmware delays, let us use a 0-order polynomial, i.e., a constant. Then

$$ \left( {\begin{array}{*{20}c} A & {{\text{e}}_{m} } \\ \end{array} } \right) \cdot \left( {\begin{array}{*{20}c} X \\ a \\ \end{array} } \right) = \Delta \varPhi + \varepsilon $$

(29)

holds. Here, $a$ is the unknown parameter (scalar), describing the phase pattern and multipath errors of the reference antenna, the remaining elements of the formula are the same as those for the TDSD algorithm.

Since the covariance matrix of measurement errors is a unit matrix, the matrix of weight coefficients is also unit, and normal equations of LSM are

$$ \left( {\begin{array}{*{20}c} {A^{{\text{T}}} A} & {A^{{\text{T}}} {\text{e}}_{m} } \\ {{\text{e}}_{m}^{{\text{T}}} A} & {{\text{e}}_{m}^{{\text{T}}} {\text{e}}_{m} } \\ \end{array} } \right) \cdot \left( {\begin{array}{*{20}c} X \\ a \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {A^{{\text{T}}} } \\ {{\text{e}}_{m}^{{\text{T}}} } \\ \end{array} } \right)\Delta \Phi $$

(30)

The covariance matrix of the expansion coefficients for PCC is a sub-matrix of the covariance matrix corresponding to the set of normal Equation (30). It can be obtained by inverting the block matrix (Bernstein 2005). By eliminating the unknown $a$ in (30), one is back to the very right-hand side of (28)

Appendix 3: Computational model of the calibration process in an open field environment

The satellite paths across the sky are taken from records of an actual observation session. Assuming a terrain underneath the antennas in the form of a perfect plane with typical parameters for soil, the reflected signals, and the related multipath errors at the antenna input is calculated as discussed in Leick et al. (2015), pp 585–597. For the calculations, the antenna gain patterns and PCC are taken from anechoic chamber measurements. With thus obtained SD, noise is added by a numerical white noise generator. Then, the SD are taken as “actual” observations by the calibration algorithm. PCC from the anechoic chamber is taken as “exact” while comparing with the thus simulated calibrations.

Appendix 4: Coordinates transformations

We express the Cartesian coordinate of a satellite p in the reference frame of the antenna under test as follows

$$ \left( {\begin{array}{*{20}c} {x_{t}^{p} } \\ {y_{t}^{p} } \\ {z_{t}^{p} } \\ 1 \\ \end{array} } \right) = T_{a} \cdot T_{r} \cdot T_{l} \cdot \left( {\begin{array}{*{20}c} {e_{l}^{p} } \\ {n_{l}^{p} } \\ {u_{l}^{p} } \\ 1 \\ \end{array} } \right) $$

(31)

where $x_{t}^{p} ,y_{t}^{p} ,z_{t}^{p}$ are the Cartesian coordinate of satellite $p$ in the coordinate system of the tested antenna, $e_{l}^{p} ,n_{l}^{p} ,u_{l}^{p}$ are the Cartesian coordinate of satellite $p$ in the local frame (east, north, up), the center of which coincides with the center of the robot’s base frame ($X_{b} ,Y_{b} ,Z_{b}$, Fig. 18), $T_{a}$ is the matrix of the homogenous transformation of the robot arm extension onto which the tested antenna is mounted, and $T_{r}$ is the matrix of homogenous transformation for the robot (Khalil and Dombre 2004). $T_{l}$ is the matrix of homogenous transformation determined by the orientation of the robot’s base frame relative to the local coordinate system

$$ T_{l} = T_{l2} \cdot T_{l1} $$

(32)

where matrices $T_{l1}$ and $T_{l2}$ are

$$ \begin{aligned} T_{l1} = \left( {\begin{array}{*{20}c} {\cos \theta_{l} + \cos^{2} \alpha_{l} \left( {1 - \cos \theta_{l} } \right)} & {\cos \alpha_{l} \;\sin \alpha_{l} \left( {1 - \cos \theta_{l} } \right)} & { - \sin \alpha_{l} \sin \theta_{l} } & 0 \\ {\cos \alpha_{l} \;\sin \alpha_{l} \left( {1 - \cos \theta_{l} } \right)} & {\cos \theta_{l} + \sin^{2} \alpha_{l} \left( {1 - \cos \theta_{l} } \right)} & {\cos \alpha_{l} \sin \theta_{l} } & 0 \\ {\sin \alpha_{l} \sin \theta_{l} } & { - \cos \alpha_{l} \sin \theta_{l} } & {\cos \theta_{l} } & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right) \hfill \\ T_{l2} = \left( {\begin{array}{*{20}c} {\cos \beta_{l} } & {\sin \beta_{l} } & 0 & 0 \\ { - \sin \beta_{l} } & {\cos \beta_{l} } & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right) \hfill \\ \end{aligned} $$

(33)

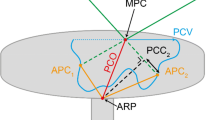
The angles $\theta_{l}$, $\alpha_{l}$, and $\beta_{l}$ in (33) are shown in Fig. 18. Shown are the local frame ENU and the base frame of the robot $X_{b} ,Y_{b} ,Z_{b}$. The angle $\theta_{l}$ is the angle for rotating the ENU system about axis c matching the line of intersecting planes east-0-north and $X_{b}$-$0$-$Y_{b}$; its orientation is determined by the angle $\alpha_{l}$. As a result of this rotation, the ENU system transforms into the frame $X_{1} ,Y_{1} ,Z_{1}$. Angle $\beta_{l}$ is the angle of rotation of the frame $X_{1} ,Y_{1} ,Z_{1}$ about axis $Z_{1}$.

Fig. 18

Robot base frame and tool frame (top). Robot base frame and local frame mutual orientation (bottom)

The matrix $T_{a}$ is

$$ T_{a} = T_{a3} \cdot T_{a2} \cdot T_{a1} $$

(34)

where matrix $T_{a1}$ characterizes the extension length and its misalignment with the $Z_{\text{tool}}$ axis of the robot tool frame, Fig. 19 (top)

$$ T_{a1} = \left( {\begin{array}{*{20}c} {\cos \theta + \cos^{2} \alpha \left( {1 - \cos \theta } \right)} & {\cos \alpha \;\sin \alpha \left( {1 - \cos \theta } \right)} & { - \sin \alpha \sin \theta } & 0 \\ {\cos \alpha \;\sin \alpha \left( {1 - \cos \theta } \right)} & {\cos \theta + \sin^{2} \alpha \left( {1 - \cos \theta } \right)} & {\cos \alpha \sin \theta } & 0 \\ {\sin \alpha \sin \theta } & { - \cos \alpha \sin \theta } & {\cos \theta } & { - L} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right) $$

(35)

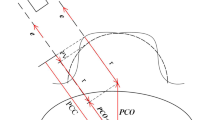
The angles $\theta$ and $\alpha$ are shown in Fig. 19 (top). The angle $\theta$ corresponds to the rotation angle of the extension axis in the plane $X_{\text{tool}} 0Y_{\text{tool}}$ around axis $b$, the direction of which is defined by angle $\alpha$, $L$ is the extension length. The angles $\theta$ and $\alpha$ are determined by measuring extension’s radial runout in the rotation of the latest robot joint (Fig. 20 left).

Fig. 19

Robot arm extension transformation angles. Transformation $T_{a1}$ (top), transformation $T_{a2}$ (middle), and transformation $T_{a3}$ (bottom)

Fig. 20

Runout measurements with variance indicator. Radial runout measurements of the robot arm extension (left). Runout measurements of extension end plane (right)

The matrix $T_{a2}$ characterizes the misalignment of the arm extension with the vertical antenna axis

$$ T_{a2} = \left( {\begin{array}{*{20}c} {\cos \beta + \cos^{2} \gamma \left( {1 - \cos \beta } \right)} & {\cos \gamma \;\sin \gamma \left( {1 - \cos \beta } \right)} & { - \sin \gamma \sin \beta } & 0 \\ {\cos \gamma \;\sin \gamma \left( {1 - \cos \left( \beta \right)} \right)} & {\cos \beta + \sin^{2} \gamma \left( {1 - \cos \beta } \right)} & {\cos \gamma \sin \beta } & 0 \\ {\sin \gamma \sin \beta } & { - \cos \gamma \sin \beta } & {\cos \beta } & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right) $$

(36)

where angles $\beta$ and $\gamma$ are shown in Fig. 19 (middle). The angle $\beta$ characterizes the rotation of extension’s end plane located within the plane $X_{1} 0Y_{1}$ around axis $c$, the direction of which is assigned by angle $\gamma$.

To determine angles $\beta$ and $\gamma$ at already known $\theta$ and $\alpha$, the runouts of a disc fixed to the extension’s end are measured at a certain known distance from the rotation axis of the latest robot joint (Fig. 20 right). The variance indicator is located within the plane $X_{\text{tool}} 0Y_{\text{tool}}$ of the robot tool frame for the 0th rotation angle of the latest robot joint. When the latest robot joint rotates, the variance indicator measures changes in coordinate Z of a certain point in the disc plane within the robot tool frame. This coordinate is determined from the equation

$$ h = \left( {\begin{array}{*{20}c} 0 & 0 & 1 & 0 \\ \end{array} } \right) \cdot T_{a2} \cdot T_{a1} \cdot T_{z} \cdot \left( {\begin{array}{*{20}c} {x_{d} } \\ 0 \\ {z_{d} } \\ 1 \\ \end{array} } \right) $$

(37)

where $h$ is the disc thickness, $x_{d}$ is the known distance from the sensor to the rotation axis, $z_{d}$ is Z-coordinate of the point of contact of sensor and disc in the robot tool frame, and $T_{z}$ is the matrix of homogenous transformation for rotation around axis Z in the robot tool frame

$$ T_{z} = \left( {\begin{array}{*{20}c} {\cos \left( \delta \right)} & {\sin \left( \delta \right)} & 0 & 0 \\ { - \sin \left( \delta \right)} & {\cos \left( \delta \right)} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array} } \right) $$

(38)

where $\delta$ is the rotation angle.

Since angles $\theta$ and $\beta$ are small (< 0.5°), first members of the expansion of trigonometric functions of these angles are used to calculate matrices $T_{a1} \cdot T_{a2}$, in (37)

$$ T_{a2} \cdot T_{a1} = \left( {\begin{array}{*{20}c} {1 - \theta \sin (\alpha )\beta \sin \gamma } & {\theta \cos (\alpha )\beta \sin \gamma } & { - \theta \sin (\alpha ) - \beta \sin \gamma } & {L\beta \sin \gamma } \\ {\theta \sin (\alpha )\beta \cos \gamma } & {1 - \theta \cos (\alpha )\beta \cos \gamma } & {\theta \cos (\alpha ) + \beta \cos \gamma } & { - L\beta \cos \gamma } \\ {\theta \sin (\alpha ) + \beta \sin \gamma } & { - \theta \cos (\alpha ) - \beta \cos \gamma } & {1 - \theta \;\beta \cos (\alpha - \beta )} & { - L} \\ 0 & 0 & 0 & 1 \\ \end{array} } \right) $$

(39)

Substituting the expression for matrix $T_{z}$ and (39) into (37), and replacing variables $x = \beta \cdot \cos \left( \gamma \right)$ and $= \beta \cdot \sin \left( \gamma \right)$, one can get the following equation

$$ \left( {\sin \left( \delta \right)x_{1} + \cos \left( \delta \right)y_{1} } \right)x_{d} + z_{d} - L - h = \left( {\sin \left( \delta \right)x_{d} - x_{1} z_{d} } \right)x + \left( {\cos \left( \delta \right)x_{d} - y_{1} z_{d} } \right)y $$

(40)

Let us designate $x_{1} = \theta \cdot \cos \left( \alpha \right)$, $y_{1} = \theta \cdot \sin \left( \alpha \right)$. In (39), there is an unknown value $z_{d}$; the beat sensor measures its variations rather than the absolute value. However, at small angles $\theta$ and $\beta$, the average value of $z_{d}$ calculated by the number of measurements in rotating the latest robot joint is approximately equal to $L + h$. With this, Equation (39) takes the following form

$$ \begin{aligned} \left( {\sin \left( {\delta_{i} } \right)x_{1} + \cos \left( {\delta_{i} } \right)y_{1} } \right)x_{d} + z_{i} - L - h & = \left( {\sin \left( {\delta_{i} } \right)x_{d} - x_{1} z_{i} } \right)x + \left( {\cos \left( {\delta_{i} } \right)x_{d} - y_{1} z_{i} } \right)y \\ i & = 1, \ldots N \\ \end{aligned} $$

(41)

Here, $\delta_{i}$ is the ith rotation angle of the latest robot joint, $z_{i} = d_{i} - d_{\text{avg}} + L + h$, $d_{i}$ is the ith measurement result of the variance indicator, $d_{\text{avg}} = \sum\nolimits_{i = 1}^{N} {d_{i} /N}$ is the average value of measurements, and N is the number of measurements. The set of Equation (41) can be solved by the LSM. As numerical simulation has shown that for angles $\theta$ and $\beta$ smaller than 1° at N about 20, the relative accuracy of determining angles $\beta$ and $\gamma$ is no worse than 1%.

The matrix $T_{a3}$ characterizes the U turn of antenna coordinate frame $X_{a} Y_{a} Z_{a}$ about its symmetry axis relative to the coordinate system $X_{2} Y_{2} Z_{2}$ by the angle χ (Fig. 19 bottom). This angle is measured during the antenna installation of the robot for every antenna sample.