Dynamics of a two-frequency parametrically driven duffing oscillator

Summary

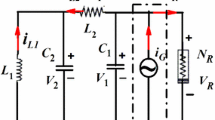
We investigate the transition from two-frequency quasiperiodicity to chaotic behavior in a model for a quasiperiodically driven magnetoelastic ribbon. The model system is a two-frequency parametrically driven Duffing oscillator. As a driving parameter is increased, the route to chaos takes place in four distinct stages. The first stage is a torus-doubling bifurcation. The second stage is a transition from the doubled torus to a strange nonchaotic attractor. The third stage is a transition from the strange nonchaotic attractor to a geometrically similar chaotic attractor. The final stage is a hard transition to a much larger chaotic attractor. This latter transition arises as the result of acrisis, the characterization of which is one of our primary concerns. Numerical evidence is given to indicate that the crisis arises from the collision of the chaotic attractor with the stable manifold of a saddle torus. Intermittent bursting behavior is present after the crisis with the mean time between bursts scaling as a power law in the distance from the critical control parameter; τ ∼ (A-A_c)^-α. The critical exponent is computed numerically, yielding the value α=1.03±0.01. Theoretical justification is given for the computed critical exponent. Finally, a Melnikov analysis is performed, yielding an expression for transverse crossings of the stable and unstable manifolds of the crisis-initiating saddle torus.