Finite-Element Dynamic Analysis of a Rotating Shaft with or without Nonlinear Boundary Conditions Subject to a Moving Load

Abstract

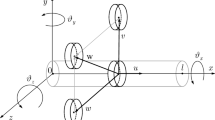
A C ⁰ continuity isoparametricfinite-element formulation is presented for the dynamic analysis of arotating or nonrotating beam with or without nonlinear boundaryconditions subject to a moving load. The nonlinear end conditions arisefrom nonlinear rolling bearings (both the nonlinear stiffness andclearance(s) are accounted for) supporting a rotating shaft. The shaftfinite-element model includes shear deformation, rotary inertia, elasticbending, and gyroscopic effect. Lagrange's equations are employed toderive system equations of motion which, in turn, are decoupled usingmodal analysis expressed in the normal coordinate representation. Theanalyses are implemented in the finite-element program ‘DAMRO 1’.Dynamic deflections under the moving load of rotating and nonrotatingsimply supported shafts are compared with those obtained using exactsolutions and other published methods and a typical coincidence isobtained. Samples of the results, in both the time and frequencydomains, of a rotating shaft incorporating ball bearings are presentedfor different values of the bearing clearance. And the results show thatsystems incorporating ball bearings with tight (zero) clearance have thesmallest amplitude-smoothest profile dynamic deflections. Moreover, fora system with bearing clearance, the vibration spectra of the shaftresponse under a moving load show modulation of the system naturalfrequencies by a combination of shaft rotational and bearing cagefrequencies. However, for a simply supported rotating shaft, the firstnatural frequency in bending dominates the response spectrum. The paperpresents the first finite-element formulation for the dynamic analysisof a rotating shaft with or without nonlinear boundary conditions underthe action of a moving load.